Тема: Окружность, круг. Циркуль. Центр, радиус. Построение окружности с помощью циркуля.

Цель:

Образовательные: Сформировать первоначальные представления об окружности и ее элементах (центре и радиусе);

познакомить с новым чертежным инструментом – циркулем и правилами техники безопасности в обращении с колющим предметом; содействовать развитию внимания, мышления, познавательной активности учащихся, их интереса к предмету, умения строить окружность и радиус с помощью циркуля и линейки;

Развивающие: развивать познавательный интерес к изучаемому предмету, умения анализировать, сравнивать и делать выводы на основании рассуждений; обогащать словарный запас учащихся, формировать умение составлять предложения на основе опорных слов;

Воспитательные: повышать познавательную активность, учебную мотивацию, способствовать развитию гармоничной личности; учить работать в паре, уважать мнение товарищей.

Коррекционно – развивающие : коррегировать и развивать познавательную деятельность обучающихся через использование упражнений на восприятие.

Ход урока.

I. Орг. момент (Эмоциональный настрой через использование стихотворения.)

- Давайте проверим, все ли готовы к уроку?

Улыбнитесь как солнышко.

Нахмурьтесь как тучки.

Заплачьте как дождики.

Удивитесь, как будто увидели радугу.

II. Проверка домашнего задания.

Рассмотрите картинки. Назовите времена года, которые на них изображены.

К каждому времени года, подберите соответствующие месяцы. (Осень – сентябрь, октябрь, ноябрь. Зима – декабрь, январь, февраль. Весна – март, апрель, май. Лето – июнь, июль, август).

Восстановите названия месяцев по порядку.

III . Устный счет.

Назовите круглые десятки.

Посчитайте от 56 до 61, от 28 до38,от 89 до 100.

46 больше 72

34 меньше 83

В числе 89 - 9 дес.

В числе 100 – 10 дес.

Из каких геометрических фигур состоят предметы на картинках.

IV . Сообщение темы урока.

1 . - У вас на партах лежат листочки,возьмите карандаш и нарисуйте круг.

Получился у вас ровный круг?

Как можно нарисовать ровный круг?

Где в жизни мы можем встретить круг?

Как вы думаете, чему будем учиться на уроке?

Мы будем учиться строить окружность с помощью циркуль.

Но сначала рассмотрим, что такое круг, а что такое окружность.

К нам в гости пришли два брата. (На магнитной доске)

Окружность и круг
Мы живём с братишкой дружно, нам так весело вдвоём,
Мы на лист поставим кружку, обведём карандашом.
Получилось то, что нужно - называется окружность.
Мой брат по рисованию себя считает мастером,
Всё, что внутри окружности, закрасил он фломастером.
Вот вам красный круг, кружок, по краю синий ободок.

Граница круга – окружность.

У круга есть одна подруга,

Знакома всем её наружность!

Она идёт по краю круга

И называется – окружность!

2.Работа в тетрадях.

- Запишите сегодняшнее число. Классная работа.

А сейчас возьмите в руки шаблон, который лежит у вас на парте и, разместив его на тетрадном листе, обведите синим карандашом. Уберите шаблон. Как называется линия синего цвета в ваших тетрадях?

Ребята, а сейчас возьмите в руки красный карандаш и закрасьте всё ,что находиться внутри синей линии в ваших тетрадях. Какая фигура получилась?

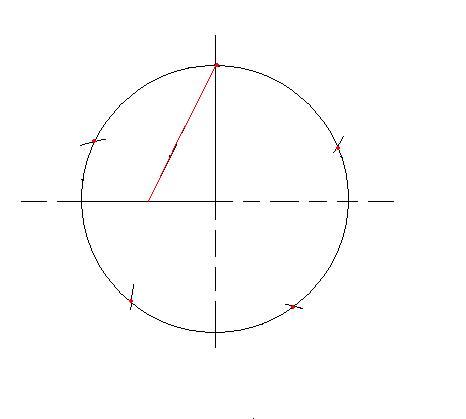
3. Построение окружности с помощью циркуля.

а) – А теперь мы будем учиться строить окружность с помощью циркуля.

Прежде чем приступить к работе с циркулем вспомним строение циркуля и правила безопасности . Циркуль состоит из двух ножек, на конце одной игла, а конце другой – грифель. За головку мы держим и поворачиваем циркуль.

б) -Возьмём циркуль и линейку, иголку циркуля приложим к 0, а другую ножку циркуля отодвинем на 2см.

А теперь перенесём циркуль в тетрадь. Постарайтесь, чтобы острый конец циркуля стоял на одном месте и не сдвигался. Строим окружность.

в) – там, где стояла иголка циркуля, поставим точку. Это центр окружности.

Теперь поставим точку в любом месте окружности и соединим центр с точкой окружности при помощи линейки.

Отрезок – это радиус окружности.

Практическая работа.

А теперь повторим эту работу. Поставим ещё одну точку в любом месте на окружности. Соединим её с центром.

Что получили?

· Ответ детей: мы получили ещё один радиус.

От окружности до центра

Мы начертим длинный ус,

Знает каждый третьеклассник,

Это точно - радиус!

V . Физкультминутка.

VI . Закрепление. Работа по учебнику.

- Откройте учебник на странице 109, прочитаем правило.

Выполним упр.2 стр.109

Выполни упр.5 стр.110

Игра “Круг или окружность”.

(Дети хлопают если это круг, показывают кольцо руками, если это окружность.) Показ картинок.

Рефлексия деятельности (итог урока).

Сегодня на уроке мы познакомились с геометрической фигурой…

Граница круга…

Окружность можно начертить при помощи…

Если вам на уроке всё удалось – покажите зелёный круг, если у вас остались неразрешённые проблемы – жёлтый круг, если вам ещё понадобится помощь – красный круг

Домашнее задание. Выучить правило стр. 109

Как найти центр круга без каких либо инструментов?
Легко! Потребуется только карандаш, ножницы и лист бумаги. Не нужна даже линейка!
Если круг уже готов, а лист бумаги имеет ровные края, то можно обойтись и без ножниц, одним карандашом, но для наглядности будем вырезать и круг, и бумага у нас будет с неровным краем, поэтому воспользуемся ножницами.
Итак, дано: круг, который нарисовали не по циркулю (там-то сразу центр отмечен иголкой), а путем обведения карандашом какого-то круглого предмета, например, тарелки, блюдца, чашки или какой-то крышки от посуды, упаковки и т.п.



Возьмем первое, что попалось под руку - подставку от цветочного горшка, стоящего рядом с компьютером. Там есть, правда, отверстие в центре и можно сразу, взяв иглу или гвоздик, отметить центр. Но мы не будем искать лёгких путей и проигнорируем такую возможность.
Рисуем на зеленом листе бумаги (взял специально для контраста обложку от тетради) окружность, обведя карандашом нашу подставку.

Вырезаем круг по нарисованной линии. Именно на нём нужно найти центр.

Берем лист бумаги, (подойдет любой, главное, чтобы был подходящим по размеру). В данном случае вполне достаточно тетрадного листочка. Если круг большой, то можно взять, например, газету большого формата. Принцип всё равно один и тот же: нам будет нужен квадратный лист бумаги, т.е ., стороны его должны быть все равны между собой.
Лист из тетради, как и стандартный лист писчей бумаги, имеют прямоугольную форму, а не квадратную (газетный лист - аналогично).

Как сделать его квадратным? - Согнуть с угла на угол так, как показано на фото.

Тот, кто хоть раз в жизни делал бумажный самолетик или какую-то другую игрушку из бумаги, хорошо представляет, как это делается.

На фото видно, что лист из тетради был вырван неаккуратно, поэтому сгибаем так, чтобы рваные края не задействовать и после сгибания листа обрезаем их ножницами. Излишек "прямоугольника" загибаем на противоположную сторону листа и места сгибов хорошенько разглаживаем, чтобы они были хорошо заметны, когда лис снова будет расправлен.

Эта линия сгиба и укажет нам диаметр круга, когда мы приложим его так, чтобы края касались двух сторон квадрата. На краях круга делаем отметки карандашом.

Используя подогнутую сторону листа, как линейку (мы договаривались в самом начале, что обходимся без неё) проводим линию, соединяющую эти метки.

Поворачиваем круг и аналогичным способом намечаем точки для проведения ещё одного диаметра.

Место пересечения этих линий и будет центром окружности. Для того, чтобы в этом убедиться, мы можем ещё несколько раз повернуть наш круг, каждый раз прикладывая его край к сторонам квадрата и проводя линии через метки сделанные напротив линии сгиба квадрата.

Все они пересекутся в центре окружности, если выполнять работу не спеша и аккуратно.
Этот принцип можно использовать в домашней мастерской, когда требуется определить центр какой-либо деревянной заготовки. И для этого легко сделать , которое намного облегчит разметку.

Есть и совсем простой способ нахождения центра плоской заготовки круглой формы.

Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.
Остается развернуть листочек, наложить его на заготовку так, чтобы края совпадали в ентре сделать пометку острым предметом, например, шилом.

И учащиеся 9 класса, группа "Теоретики"

Тема исследования группы

Изучение основного теоретического материала, необходимого при решении задач по теме "Правильные многоугольники",

а также в задачах на построение правильных многоугольников.

Цели исследования

Ответить на вопросы:

1) Что мы знаем о правильных многоугольниках?

2) Какие формулы необходимы при решении задач на нахождение элементов правильного

многоугольника и его площади?

3) Как построить правильный многоугольник?

Результаты исследования

Определение:

Правильным называется выпуклый многоугольник, у которого все углы и все стороны равны между собой.

Основные формулы:

1. Сторона правильного многоугольника а = 2R sin 180/n

2. Радиус вписанной окружности r = R cos 180/n

3. Площадь правильного многоугольника S = 1/2 Pr

Геометрические задачи на построение с помощью циркуля и линейки зародились еще в древней Греции во времена Евклида и Платона. Еще в те времена, математики умели строить с помощью циркуля и линейки правильные треугольники, пятиугольники и квадраты. Более того, они умели с помощью циркуля и линейки делить угол пополам, поэтому они умели строить и правильные 6-ти, 10-ти и 15-ти угольники и все правильные n-угольники. Очень важно, что с помощью линейки проводятся только отрезки прямых, а длины отрезков измеряются с помощью циркуля, а не делений на линейке. Так, используя эти инструменты можно построить отрезок, длина которого выражается числом, полученным из 1 с помощью четырех арифметических действий (сложения, вычитания, умножения, деления) и извлечением квадратного корня. Т.е. вначале есть только отрезок, длина которого принимается за 1. Тогда можно построить отрезок, длина которого равна рациональному числу или квадратному корню из рационального числа. Далее, если отрезок длины а уже построен с помощью циркуля и линейки, то можно построить с помощью этих инструментов отрезок длины b, если число b выражается через а с помощью арифметических действий и квадратного корня. Говорят, что такое число выражается в квадратных радикалах. Таким образом, с помощью циркуля и линейки можно построить отрезок, длина которого выражается в квадратных радикалах. Все это знали еще математики древней Греции. Задачу построения других правильных многоугольников (или доказательство невозможности таких построений) не могли решить в течение двух последующих тысячелетий, а решена она была немецким студентом филологического факультета Гёттингенского университета Карлом Фридрихом Гауссом в 1796 году. В то время Гауссу было 18 лет и он разрывался между занятиями филологией и математикой и не мог сделать окончательного выбора. Решение древней задачи помогло ему сделать окончательный выбор в пользу (и на пользу) математики. Страшно даже подумать, насколько бы затормозилось развитие математики, останься Гаусс филологом! До сих пор математики всего мира называют Гаусса королем математики.

Деление окружности на четыре, восемь равных частей. Построение правильного четырехугольника и восьмиугольника.

Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 64).

Для того чтобы разделить окружность на восемь равных частей, необходимо разделить на две равные части дугу, равную 1/4 окружности. Таким образом получим дугу, равную 1/8 окружности (А4 = A3). Раствором циркуля, равным A3 или А4, нанесем засечки на окружности, разделив ее тем самым на восемь равных частей. Последовательно соединив засечки отрезками прямых, получим правильный восьмиугольник (рис. 64).

Построить правильный шестиугольник, сторона которого равна данному отрезку.

Для решения задачи воспользуемся формулой а=Р Пусть ПК - данный отрезок. Построим окружность радиуса ПК и отметим на ней произвольную точку А1. Затем, не меняя раствора циркуля, построим на этой окружности точки А2,А3, А4.....А6 так, чтобы выполнялись равенства - А1А2=А3А4=А5А6. Соединяя последовательно данные точки отрезками, получим искомый правильный шестиугольник А1А2А3А4А5А6.

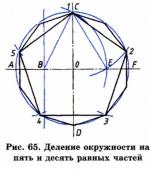
Деление окружности на пять и десять равных частей. Построение правильных пятиугольника и десятиугольника.

Чтобы разделить окружность на пять равных частей, находим середину радиуса окружности ОА. Приняв точку В за центр, проведем дугу, радиус которой равен длине отрезка ВС, до пересечения ее с горизонтальным диаметром в точке Е. Отрезок СЕ есть сторона пятиугольника. Отрезок ОЕ соответствует стороне правильного вписанного десятиугольника. Отложив величину, равную 1/5 и 1/10 окружности, разделим ее на пять и десять равных частей. Соединив последовательно засечки (вершины n-угольника) отрезками прямых, получим правильные пяти- и десятиугольники (рис. 65).

Деление окружности на три, шесть, двенадцать равных частей. Построение правильных многоугольников.

Деление окружности на три равные части производится следующим образом. Точка С (рис. 66) принимается за центр, из которого проводится дуга, радиус которой равен радиусу окружности. Проведенная дуга пересечет окружность в точках 2 и 3. Дуги 1-2, 1-3, 2-3 являются третьей частью окружности. Соединив точки 1, 2 и 3, получим правильный треугольник.

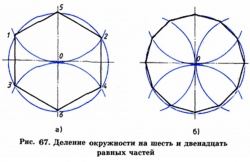
Чтобы разделить окружность на шесть равных частей, от любой ее точки отложим отрезки, равные радиусу окружности (R). Полученные дуги делят окружность на шесть равных частей. Приняв точки 1, 2, 3, 4, 5, 6 за вершины шестиугольника, соединим их отрезками прямых, как показано на рис. 67, а. Таким образом, построим правильный шестиугольник.

Деление окружности на двенадцать равных частей основано на откладывании от любой ее точки отрезков, равных половине радиуса окружности (R/2). Полученные дуги разделят окружность на двенадцать равных частей. Приняв каждую засечку за вершину двенадцатиугольника и последовательно соединив их, получим правильный двенадцатиугольник и определение величины радиуса (рис. 67, б).

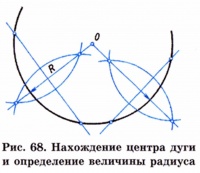
Нахождение центра дуги и определение величины радиуса.

В практике выполнения чертежей бывает необходимо найти центр дуги и определить величину ее радиуса. Для этого проводят две непараллельные хорды и восставляют перпендикуляры к их серединам. Точка пересечения перпендикуляров (точка О) есть центр дуги (рис. 68). От центра замеряют величину радиуса дуги.

Если построен какой-нибудь правильный n-угольник, то с помощью циркуля и линейки можно построить правильный 2n-угольник. Опишем около данного многоугольника А1, А2… Аn oкружность. Для этого построим серединные перпендикуляры a и b к oтрезкам А1 А2 и А2 А3 (на рисунке n = 4). Они пересекаются в некоторой точке О. Окружность с центром О радиуса ОА1 является описанной около многоугольника А1 А2…Аn. Построим теперь середины B1, B2, …, Bn соответственно дуг А1 А2, А2А3,…, Аn А1 следующим образом. Точки B1и B2 получаются как точки пересечения прямых а и b с дугами А1 А2 и А2 А3. Для построения точки B3 проведём oкружность с центром А3 радиуса А3 B2. Одна из точек пересечения этой oкружности с описанной окружностью есть точка B2, а другая - искомая точка B3. Аналогично строятся точки B4,…, Bn. Соединив каждую из точек B1,B2,…, Bn отрезками с концами соответствующей дуги, получим 2n-угольник А1В1А2В2А3… Аn Bn, который является правильным в силу теоремы о вписанном в окружность многоугольнике

На рисунке по данному правильному четырёхугольнику А1А2А3А4 построен правильный восьмиугольник А1В1А2…В4. Итак, если мы можем построить циркулем и линейкой правильный n-угольник, где n - данное натуральное число, то можно построить правильные 2n-угольник, 4n-угольник и, вообще, (2^k*n)-угольник, где k - любое натуральное число. Знаменитый немецкий математик К. Ф. Гаусс (1777- 1855) доказал следующую интересную теорему: Построение правильного n-угольника с помощью линейки и циркуля возможно тогда и только тогда, когда число n имеет следующее разложение на множители: n=2^m*2*p1*p2...ps, где m-целое неотрицательное число, а p1, p2,...,ps-различные между собой простые числа вида 2^2^k+1. Рассмотрим примеры применения этой теоремы. При m=0, s=1 число n имеет вид n=2^2^k +1. Для значений k, равных 0, 1, 2, 3, 4, получаем n=3, n=5, n=17, n=257, n=65 537. При m=0, s=2 имеем n=p1p2. Если, например, р1=3, р2=5, то n=15. Значит, согласно теореме Гаусса, можно построить циркулем и линейкой правильный 15-угольник, в чём мы убедимся позже. Число 7 простое, но оно не является числом вида 2^2^k +1, поэтому с помощью циркуля и линейки нельзя построить правильный семиугольник. Точно так же нельзя построить правильный девятиугольник. Отметим, наконец, что число 360=2^3*3^2*5 не удовлетворяет теореме Гаусса, поскольку простое число 3 входит сомножителем два раза. Следовательно, циркулем и линейкой нельзя построить правильный 360-угольник. Другими словами, нельзя разделить окружность на 360 равных частей и поэтому циркулем и линейкой нельзя построить угол в 1°.

Задача №1. Построение правильного шестиугольника и треугольника.

Согласно формуле аn= 2R*sin180°/n сторона АВ правильного шестиугольника равна радиусу R описанной окружности . Поэтому, если задан произвольный отрезок PQ, то для построения правильного шестиугольника, стороны которого равны PQ, достаточно построить окружность радиуса PQ, взять на ней произвольную точку А и, не меняя раствора циркуля , отметить на этой окружности последовательно точки B, C, D, E, F так, чтобы AB=BC=…=EF=PQ. Проведя затем отрезки AB, BC, CD, DE, EF, FA, получим шестиугольник ABCDEF, который согласно теореме о правильном многоугольнике является правильным, причем его стороны равны отрезку PQ.

Пусть w-данная окружность с центром в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр , который пересечет окружность w в двух точках В и D.Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат.

Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А1А3А5А7-квадрат, потом построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1, которые прересекут окружность в точках А2, А4, А6, А8 соответственно, затем последовательно соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2...А8-искомый восьмиугольник.

Построения с помощью циркуля и линейки - раздел евклидовой геометрии, известный с античных времён.

В задачах на построение возможны следующие операции:

Простой пример

• Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку пересечения двух построенных линий.
• С помощью циркуля провести окружность с центром в построенной точке с радиусом, равным расстоянию между двух уже построенных точек.
• С помощью линейки провести прямую, проходящую через две построенные точки.

При этом циркуль и линейка считаются идеальными инструментами, в частности

• Линейка не имеет делений и имеет только одну сторону бесконечной длины.
• Циркуль может иметь сколь угодно большой раствор.

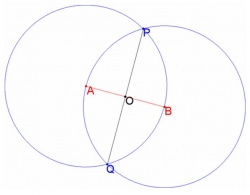
Задача 3. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружность с центром в точке A радиусом AB.
• Проводим окружность с центром в точке B радиусом AB.
• Находим точки пересечения P и Q двух построенных окружностей.
• Линейкой проводим отрезок, соединяющий точки P и Q.
• Находим точку пересечения AB и PQ. Это - искомая середина отрезка AB.

Правильные многоугольники

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э. Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа). 2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A. 3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B. 4. Постройте точку C посередине между O и B. 5. Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D. 6. Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F. 7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G. 8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H. 9. Постройте правильный пятиугольник AEGHF.

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

• Трисекция угла - разбить произвольный угол на три равные части.
• Удвоение куба - построить отрезок, являющийся ребром куба в два раза большего объёма, чем куб с данным ребром.
• Квадратура круга - построить квадрат, равный по площади данному кругу.

Только в XIX веке было доказано, что все три задачи не разрешимы циркулем и линейкой . Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

Другая известная неразрешимая с помощью циркуля и линейки задача - построение треугольника по трём заданным.

1. Колмогоров А.Н. Паркеты из правильных многоугольников. Журнал "Квант" №3, 1970 г.

2. Шашкин Ю.А. Паркеты.

3. Совертков П.И., Слива М.В.,Хохлов Д.Н. Геометрический паркет на экране компьютера. Журнал "Информатика и образование", 9-2002.

4. По материалам книги: У. Болл, Г. Коксетер. Математические эссе и развлечения. Пер. с англ. - М.: "Мир", 1986. - 474 с. с ил.

Под редакцией Иваницкой В.П. - М.: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959. - 272 c.
Скачать (прямая ссылка): egnnsholaster1959.djvu Предыдущая 1 .. 50 > .. >> Следующая

§ 53. Построения одним циркулем

В § 14 мы уже говорили о построениях при помощи одного циркуля. Докажем теперь, что все построения циркулем и линейкой могут быть выполнены одним циркулем. Для этого воспользуемся рассмотренным нами в главе VI преобразованием инверсии.

Прежде всего покажем, как одним циркулем построить точку, инверсную данной относительно данной окружности.

Пусть А - данная точка, а О - окружность инверсии.

Случай 1. OA > у, где г-радиус окружности инверсии (черт. 150 а, 150 б).

Строим окружность радиуса АО с центром в точке А\ из точек пересечения ее с окружностью О (точки P и Q)9

как из центров, строим окружности радиуса г. Эти две последние окружности, кроме точки О, пересекутся еще в некоторой точке А"", которая будет искомой.

Действительно, точки O9 A Yi А" лежат на одной прямой, как точки, равноудаленные от точек PhQ. Кроме того, AOPA оо дОРЛ", так как эти треугольники равнобедренные и имеют общий угол при вершине О. Отсюда:

или OA" OA = OP2 = г2, т. е. А и А" - взаимно обратные точки.

Черт. 150 а

Черт. 150 б

Случай 2. OA <

Подберем такое натуральное число /г, чтобы п - OA > у (что

всегда возможно в силу аксиомы Архимеда). На луче OA возьмем точку В так, чтобы OB = п - OA (черт. 151). Строим точку S", инверсную точке В, и на луче OA бе-

точку А" так, чтобы = п-ОВ. Тогда имеем:

OA"= OA - п-ОВ"= = {п-ОА)-ОВ" -= = OB-OB" =г\

т. е. точка А" инверсна Черт. 151

Так как при помощи одного циркуля мы можем удваивать отрезок (§ 14), то все построения в данном случае мы можем осуществить тоже при помощи одного циркуля.

Покажем теперь, как при помощи одного циркуля построить центр окружности, проходящей через три данные точки O1 А и В (черт. 152).

Построим окружность с центром в точке О и примем ее за окружность инверсии. Построим затем точки А" и В", инверсные данным точкам А и В (что можно выполнить одним циркулем). В целях упрощения чертежа возьмем окружность инверсии, проходящей через точку А. Тогда точки А я А" совпадают. При помощи одного циркуля построим точку M1 симметричную точке О относительно прямой AB". Наконец, строим точку /С, инверсную точке М.

По построению точки O1 К и M лежат на одной прямой и OK- OM = OA2. Отсюда:

Треугольники OAK и OAM подобны, так как ^AOM у них общий, а стороны, заключающие его, пропорциональ-

ны. Поэтому ^ OAK = ^OMA. По построению OA = MA. Следовательно, OK = AK- Рассматривая треугольники OMB" и OKB1 совершенно также докажем, что они подобны и KB = OK- Таким образом, точка К является центром искомой окружности.

Чтобы построить окружность, инверсную данной окружности, возьмем на последней три произвольные точки А, В и С, построим инверсные им точки А", В" и С и проведем через них окружность. Все необходимые при этом построения могут быть выполнены одним циркулем.

Если дана прямая двумя точками А и B1 то для построения окружности, ей инверсной (предполагаем, что прямая AB не проходит через центр инверсии), строим точки А" и В", взаимно обратные точкам А и B1 и проводим окружность через точки А", В" и центр инверсии. Все необходимые при этом построения могут быть также выполнены одним циркулем.

Рассмотрим теперь задачу о построении одним циркулем точек пересечения окружности С и прямой, заданной точками А и В.

Возьмем произвольную окружность так, чтобы ее центр не лежал на прямой AB и на окружности C1 и примем эту окружность за окружность инверсии. Строим затем окружности С и К"инверсные данной окружности С и данной прямой AB. Пусть M" и N" - точки пересечения окружностей С и К". Тогда точки MnN1 обратные им, являются искомыми. Эти точки, следовательно, можно построить, применяя только циркуль.

Если даны две прямые AB и CD1 заданные точками A1 BnC1D1 то строим окружности, им инверсные, находим точку их пересечения M", отличную от центра инверсии, и строим точку M1 обратную точке ЛГ. Точка M будет искомой точкой пересечения прямых AB и CD.

Отсюда вытекает упомянутая в§ 14 теорема Мор а- Маскерони: Все задачи на построение, разрешимые циркулем и линейкой, разрешимы также одним циркулем.

Из доказательства данной теоремы вытекает и общий метод решения задач одним циркулем. Само собой разумеется, что конкретные задачи могут иметь более простые решения.

При нахождении точек пересечения окружности и прямой удобно данную окружность принять за окружность инверсии. Окружность, инверсная прямой AB, пересекается

с окружностью С в тех же точках X и Y1 что и прямая AB (черт. 153). Для построения ее центра строим точку M1 симметричную центру С относительно прямой AB1 и точку /С, инверсную М. Точка К является центром окружности, инверсной прямой AB. Остается построить эту окружность (ее радиус - отрезок КС) и точки ее пересечения с данной окружностью.

Данное построение, как легко убедиться, обосновано Черт. 153 выше при решении задачи о построении окружности, проходящей через три данные точки. В случае, если центр окружности лежит на прямой AB1 данное построение неприменимо.

Инструкция

Обозначьте точки, в которых дуга пересекает окружность как C и C1.

С помощью линейки соедините точки C и C1 отрезком.

Точку, в которой отрезок между точками C и C1 пересекает диаметр окружности AB, отметьте как точку D.

С помощью циркуля отложите расстояние между точками C и D по окружности 7 раз. Для этого поместите острие циркуля в произвольное место на окружности, например в точку A. Отметьте чертежной частью циркуля одну любую точку на окружности. Поместите острие циркуля в отмеченную точку и точно также отметьте следующую точку. Разметьте таким способом всю длину окружности.

Соедините с помощью линейки и карандаша все отмеченные точки на окружности с её центром в точке O.

Для построения правильных многоугольников очень часто используется прием разбивки окружности на равные части. В принципе, окружность можно делить и при помощи транспортира. Но чаще всего такой прием оказывается неудобным.

Инструкция

Разбить окружность на четыре равные части очень просто, это тривиальная задача. Для этого нужно просто провести две перпендикулярные друг другу осевые линии. Точки на пересечении этих линий с окружность ю и разделят ее на четыре части. Чаще возникает необходимость разделить окружность не на четыре, а на восемь равных частей. Для того, чтобы это сделать, нужно будет разделить дугу, которая составляет одну четверть окружности, на две равные части. Затем возьмите циркуль и разведите его на расстояние, которое на изображении обозначено красным цветом. Теперь осталось просто отложить это расстояние от каждой из полученных ранее четырех точек.

Для того чтобы разбить окружность на три равные части, разведите ножки циркуля на радиус окружности. После этого в любую точку пересечения осевых линий и окружности установите иглу циркуля. Проведите тонкой линией вспомогательную окружность . Три равные части образуются точками пересечения основной и вспомогательной окружностей, а так же точкой, которая лежит на осевой линии, вернее на ее противоположном конце.

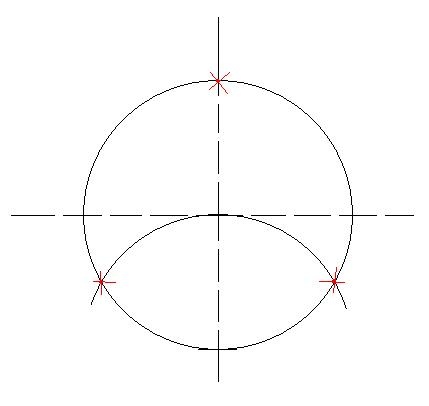
А если нужно разделить окружность на шесть равных частей, то нужно проделать практически все то же самое. Отличие состоит лишь в том, что эти действия необходимо повторить и для другой осевой линии. В этом случае получится сразу шесть точек на окружности, как показано на рисунке.

Очень часто возникает необходимость разделить окружность на пять равных частей. Это сделать тоже не сложно. Сначала нужно разделить на осевой линии радиус на две равные части. Именно в эту точку и нужно поставить иглу циркуля. Грифель же необходимо отвести до точки пересечения окружности и перпендикулярной этому радиусу осевой линии. Наглядно это можно увидеть рисунке. На нем это расстояние изображено красным. Это расстояние откладывайте на окружности. Начинать нужно с осевой линии, а затем иглу переносить в новую получившуюся точку пересечения. Чтобы разбить окружность на десять частей повторите все вышеописанные действия зеркально.

Разделение окружности на равные части обычно используется для построения правильных многоугольников. В принципе, можно делить окружность на части с помощью транспортира, но иногда это неудобно и неточно.

Инструкция

Чтобы разделить окружность на шесть частей, проделайте то же самое для другой осевой. Тогда получится шесть точек на окружности.

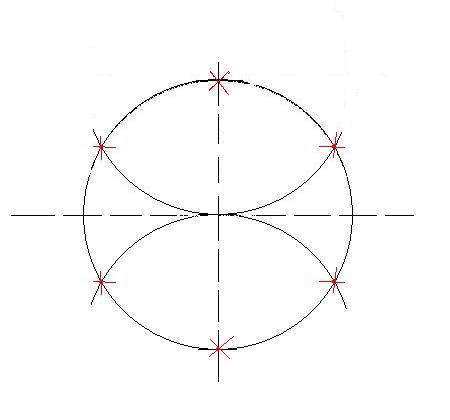
Деление окружности на четыре части - тривиальная задача. Четыре точки на пересечении двух перпендикулярных осевых и окружности будут делить эту окружность на четыре равные части. Чтобы разделить окружность на 8 частей, надо разделить дугу, соответствующую 1/4 окружности пополам. Затем развести циркуль на расстояние , обозначенное красным на рисунке, и отложить это расстояние от уже полученных четырех точек.

Чтобы разделить окружность на пять равных частей, для начала разделите радиус на осевой линии пополам. В эту точку установите иглу циркуля, а грифель отведите до пересечения перпендикулярной этому радиусу осевой и окружности. На рисунке это расстояние показано красным. Откладывайте это расстояние на окружности, начиная с осевой, а потом перенося циркуль в получившуюся точку пересечения.
Повторите эти все действия зеркально, чтобы разбить окружность на 10 одинаковых частей.

Видео по теме

Источники:

• как разделить окружность на 8 частей

Смена операционной системы - процесс довольно долгий и затруднительный, если не иметь навык продвинутого пользователя в плане обращения с компьютерными программами. Однако можно произвести переустановку ОС, следуя некоторым простым инструкциям.

Вам понадобится

• Компьютер с подключенным интернетом, флешка или диск с ОС.

Инструкция

Прочитайте о системных требованиях, предъявляемых Windows 7 компьютерному оборудованию. Дело в том, что технические возможности вашего компьютера могут быть недостаточными для нормальной работы данной операционной системы. Как известно, с переходом компании Microsoft на операционные системы семейства Windows 7 требования к оборудованию резко возросли в связи с улучшенными визуальными эффектами интерфейса ОС.

Определите системные параметры вашего компьютера. Для этого откройте меню «Пуск», далее «Мой компьютер». Кликните по кнопке «Параметры системы». В появившемся окне вы можете увидеть основные системные характеристики компьютера, то есть частоту процессора, его модель, объем оперативной памяти. Сравните данные параметры с теми, что предъявлены разработчиками Windows 7. Если производительность вашего компьютера недостаточна, то производить установку не рекомендуется.

Используйте CD-диск с операционной системой для ее установки, если таковой имеется. Если же ОС находится на компьютере в виде файла-образа, то необходимо предварительно записать его на диск. Записывая ОС на пустой CD-R, убедитесь, что создается загрузочный диск. Также вы можете создать загрузочную флешку и устанавливать ОС с нее. Это позволит сделать процесс установки более скоростным. Для этой цели вам понадобится программа UltraISO. Также с ее помощью вы можете записать файл-образ операционной системы на диск, если располагаете записывающим дисководом. Обратите внимание на то, что размер памяти диска или флешки должен быть не меньше размера копии ОС.

Вставьте диск или флешку с ОС в дисковод и перезагрузите компьютер. В начале его загрузки нажмите клавишу F2. Откроется программа BIOS, позволяющая устанавливать параметры загрузки. Перейдите в раздел Boot. Здесь вы увидите список устройств, к которым обращается компьютер при загрузке, упорядоченный в порядке снижения приоритета загрузки. Поставьте первым в списке ваш диск или флешку, а на второе место – жесткий диск. Нажмите клавишу F10 для сохранения параметров. Перезагрузите компьютер.

Вопрос о том, чему равна величина окружности планеты Земля, интересовал ученых очень давно. Так, первые измерения этого параметра были осуществлены еще в Древней Греции.

Измерение окружности

О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли - экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному меридиану , полученная цифра будет точно такой же.

Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени - Французской академии - придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.

В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя длинами - она составила 21,4 километра.

Длина окружности

В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.

Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.

Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, такое различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.

Источники:

• как разделить квадрат на 7 квадратов