The discriminant is an ambiguous term. This article will discuss the discriminant of a polynomial, which allows one to determine whether a given polynomial has real solutions. The formula for the square polynomial is found in the school course of algebra and analysis. How to find discriminant? What is needed to solve the equation?

A square polynomial or equation of the second degree is called   i * w ^ 2 + j * w + k equal to 0, where “i” and “j” are the first and second coefficients, respectively, “k” is a constant, which is sometimes called a “free term”, and “w” is a variable. Its roots will be all the values \u200b\u200bof the variable, at which it turns into identity. It is possible to rewrite such an equality as the product of i, (w - w1) and (w - w2) equal to 0. In this case, it is obvious that if the coefficient “i” does not vanish, then the function on the left side will become zero only if if x takes the value w1 or w2. These values \u200b\u200bare the result of equating the polynomial to zero.

To find the value of the variable at which the square polynomial vanishes, we use an auxiliary construction based on its coefficients and called the discriminant. This design is calculated according to the formula D equals j * j - 4 * i * k. Why is it used?

1. She says whether there are valid results.
2. She helps them calculate.

As this value shows the presence of material roots:

• If it is positive, then you can find two roots in the field of real numbers.
• If the discriminant is equal to zero, then both solutions coincide. We can say that there is only one solution, and it is from the field of real numbers.
• If the discriminant is less than zero, then the polynomial has no real roots.

Settlement options for fixing material

For the sum (7 * w ^ 2; 3 * w; 1) equal to 0   we calculate D by the formula 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 we get -19. A discriminant value below zero indicates the absence of results on the real line.

If we consider 2 * w ^ 2 - 3 * w + 1 equivalent 0, then D is calculated as (-3) squared minus the product of numbers (4; 2; 1) and equals 9 - 8, that is 1. A positive value indicates two results on the real line.

If we take the sum (w ^ 2; 2 * w; 1) and equate to 0, D is calculated as two squared minus the product of numbers (4; 1; 1). This expression will simplify to 4 - 4 and vanish. It turns out that the results are the same. If you look closely at this formula, it will become clear that this is a “full square”. Therefore, the equality can be rewritten in the form (w + 1) ^ 2 \u003d 0. It became obvious that the result in this problem is “-1”. In a situation if D is 0, the left side of the equation will always turn out according to the “squared sum” formula.

Using the discriminant in calculating roots

This auxiliary construction not only shows the number of material solutions, but also helps to find them. The general calculation formula for the equation of the second degree is as follows:

w \u003d (-j +/- d) / (2 * i), where d is a discriminant of degree 1/2.

Suppose the discriminant is below zero, then d is imaginary and the results are imaginary.

D is zero, then d equal to D to the degree 1/2 is also zero. Solution: -j / (2 * i). Again we consider 1 * w ^ 2 + 2 * w + 1 \u003d 0, we find the results equivalent to -2 / (2 * 1) \u003d -1.

Suppose D\u003e 0, so d is a real number, and the answer here splits into two parts: w1 \u003d (-j + d) / (2 * i) and w2 \u003d (-j - d) / (2 * i) . Both results will be valid. Take a look at 2 * w ^ 2 - 3 * w + 1 \u003d 0. Here, the discriminant and d are units. It turns out that w1 is (3 + 1) divided by (2 * 2) or 1, and w2 is (3 - 1) divided by 2 * 2 or 1/2.

The result of equating the square expression to zero is calculated according to the algorithm:

1. Determining the number of valid decisions.
2. Calculation d \u003d D ^ (1/2).
3. Finding the result in accordance with the formula (-j +/- d) / (2 * i).
4. Substitution of the result into the original equality for verification.

Some special cases

Depending on the coefficients, the solution may be somewhat simplified. Obviously, if the coefficient in front of the variable is equal to zero to the second degree, then linear equality is obtained. When the coefficient before the variable is zero in the first degree, then two options are possible:

1. the polynomial decomposes into a difference of squares with a negative free term;
2. with a positive constant, real solutions cannot be found.

If the free term is zero, then the roots will be (0; -j)

But there are other special cases that simplify finding a solution.

The reduced equation of the second degree

Referred to as such a square trinomial, where the coefficient in front of the senior term is one. For this situation, the Vieta theorem is applicable, stating that the sum of the roots is equal to the coefficient for the variable in the first degree, multiplied by -1, and the product corresponds to the constant “k”.

Therefore, w1 + w2 equals -j and w1 * w2 equals k if the first coefficient is one. To verify the correctness of such a representation, we can express w2 \u003d -j - w1 from the first formula and substitute it into the second equality w1 * (-j - w1) \u003d k. As a result, the initial equality w1 ^ 2 + j * w1 + k \u003d 0 is obtained.

It is important to notethat i * w ^ 2 + j * w + k \u003d 0 can be reduced by dividing by “i”. The result will be: w ^ 2 + j1 * w + k1 \u003d 0, where j1 is j / i and k1 is k / i.

Take a look at the already solved 2 * w ^ 2 - 3 * w + 1 \u003d 0 with the results w1 \u003d 1 and w2 \u003d 1/2. It is necessary to divide it in half, as a result w ^ 2 - 3/2 * w + 1/2 \u003d 0. Let us verify that the conditions of the theorem are valid for the results found: 1 + 1/2 \u003d 3/2 and 1 * 1/2 \u003d 1 / 2.

Even second multiplier

If the factor of a variable in the first degree (j) is divisible by 2, then we can simplify the formula and look for a solution in a quarter of the discriminant D / 4 \u003d (j / 2) ^ 2 - i * k. it turns out w \u003d (-j +/- d / 2) / i, where d / 2 \u003d D / 4 to the power of 1/2.

If i \u003d 1, and the coefficient j is even, then the solution will be the product of -1 and half of the coefficient for the variable w, plus / minus the root of the square of this half minus the constant “k”. Formula: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.

Higher Discriminant Order

The discriminant of the trinomial of the second degree considered above is the most used particular case. In the general case, the discriminant of a polynomial is multiplied squares of the differences of the roots of this polynomial. Therefore, a discriminant equal to zero indicates the presence of at least two multiple solutions.

Consider i * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0.

D \u003d j ^ 2 * k ^ 2 - 4 * i * k ^ 3 - 4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Let's say the discriminant is greater than zero. This means that there are three roots in the field of real numbers. At zero there are multiple solutions. If D< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.

Video

Our video will talk in detail about the calculation of the discriminant.

Didn't get an answer to your question? Suggest a topic to the authors.

For example, for the trinomial \\ (3x ^ 2 + 2x-7 \\), the discriminant will be \\ (2 ^ 2-4 \\ cdot3 \\ cdot (-7) \u003d 4 + 84 \u003d 88 \\). And for the trinomial \\ (x ^ 2-5x + 11 \\), it will be equal to \\ ((- 5) ^ 2-4 \\ cdot1 \\ cdot11 \u003d 25-44 \u003d -19 \\).

The discriminant is denoted by the letter \\ (D \\) and is often used in solving. Also, by the value of the discriminant, you can understand how the graph looks approximately (see below).

The discriminant and the roots of the equation

The value of the discriminant shows the number of quadratic equations:
   - if \\ (D \\) is positive, the equation will have two roots;
   - if \\ (D \\) is equal to zero - only one root;
   - if \\ (D \\) is negative, there are no roots.

You don’t need to learn this, it’s easy to come to this conclusion, just knowing that from the discriminant (that is, \\ (\\ sqrt (D) \\) is included in the formula for calculating the roots of the equation: \\ (x_ (1) \u003d \\) \\ (\\ .

If the discriminant is positive

In this case, the root of it is some positive number, which means that \\ (x_ (1) \\) and \\ (x_ (2) \\) will be different in value, because in the first formula, \\ (\\ sqrt (D) \\) is added , and in the second - it is deducted. And we have two different roots.

Example : Find the roots of the equation \\ (x ^ 2 + 2x-3 \u003d 0 \\)
Decision :

Answer : \\ (x_ (1) \u003d 1 \\); \\ (x_ (2) \u003d - 3 \\)

If the discriminant is zero

And how many roots will there be if the discriminant is zero? Let's reason.

The root formulas look like this: \\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) and \\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\). And if the discriminant is zero, then the root of it is also zero. Then it turns out:

\\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + 0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)

\\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b- \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b-0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)

That is, the values \u200b\u200bof the roots of the equation will coincide, because adding or subtracting zero does not change anything.

Example : Find the roots of the equation \\ (x ^ 2-4x + 4 \u003d 0 \\)
Decision :

\\ (x ^ 2-4x + 4 \u003d 0 \\)		We write out the coefficients:
\\ (a \u003d 1; \\) \\ (b \u003d -4; \\) \\ (c \u003d 4; \\)		We calculate the discriminant by the formula \\ (D \u003d b ^ 2-4ac \\)
\\ (D \u003d (- 4) ^ 2-4 \\ cdot1 \\ cdot4 \u003d \\) \(=16-16=0\)		Find the roots of the equation
\\ (x_ (1) \u003d \\) \\ (\\ frac (- (- 4) + \\ sqrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\)    \\ (x_ (2) \u003d \\) \\ (\\ frac (- (- 4) - \\ sqrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\)		We got two identical roots, so it makes no sense to write them separately - we write as one.

Answer : \\ (x \u003d 2 \\)

The discriminant is an ambiguous term. This article will discuss the discriminant of a polynomial, which allows one to determine whether a given polynomial has real solutions. The formula for the square polynomial is found in the school course of algebra and analysis. How to find discriminant? What is needed to solve the equation?

A square polynomial or equation of the second degree is called   i * w ^ 2 + j * w + k equal to 0, where “i” and “j” are the first and second coefficients, respectively, “k” is a constant, which is sometimes called a “free term”, and “w” is a variable. Its roots will be all the values \u200b\u200bof the variable, at which it turns into identity. It is possible to rewrite such an equality as the product of i, (w - w1) and (w - w2) equal to 0. In this case, it is obvious that if the coefficient “i” does not vanish, then the function on the left side will become zero only if if x takes the value w1 or w2. These values \u200b\u200bare the result of equating the polynomial to zero.

To find the value of the variable at which the square polynomial vanishes, we use an auxiliary construction based on its coefficients and called the discriminant. This design is calculated according to the formula D equals j * j - 4 * i * k. Why is it used?

1. She says whether there are valid results.
2. She helps them calculate.

As this value shows the presence of material roots:

• If it is positive, then you can find two roots in the field of real numbers.
• If the discriminant is equal to zero, then both solutions coincide. We can say that there is only one solution, and it is from the field of real numbers.
• If the discriminant is less than zero, then the polynomial has no real roots.

Settlement options for fixing material

For the sum (7 * w ^ 2; 3 * w; 1) equal to 0   we calculate D by the formula 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 we get -19. A discriminant value below zero indicates the absence of results on the real line.

If we consider 2 * w ^ 2 - 3 * w + 1 equivalent 0, then D is calculated as (-3) squared minus the product of numbers (4; 2; 1) and equals 9 - 8, that is 1. A positive value indicates two results on the real line.

If we take the sum (w ^ 2; 2 * w; 1) and equate to 0, D is calculated as two squared minus the product of numbers (4; 1; 1). This expression will simplify to 4 - 4 and vanish. It turns out that the results are the same. If you look closely at this formula, it will become clear that this is a “full square”. Therefore, the equality can be rewritten in the form (w + 1) ^ 2 \u003d 0. It became obvious that the result in this problem is “-1”. In a situation if D is 0, the left side of the equation will always turn out according to the “squared sum” formula.

Using the discriminant in calculating roots

This auxiliary construction not only shows the number of material solutions, but also helps to find them. The general calculation formula for the equation of the second degree is as follows:

w \u003d (-j +/- d) / (2 * i), where d is a discriminant of degree 1/2.

Suppose the discriminant is below zero, then d is imaginary and the results are imaginary.

D is zero, then d equal to D to the degree 1/2 is also zero. Solution: -j / (2 * i). Again we consider 1 * w ^ 2 + 2 * w + 1 \u003d 0, we find the results equivalent to -2 / (2 * 1) \u003d -1.

Suppose D\u003e 0, so d is a real number, and the answer here splits into two parts: w1 \u003d (-j + d) / (2 * i) and w2 \u003d (-j - d) / (2 * i) . Both results will be valid. Take a look at 2 * w ^ 2 - 3 * w + 1 \u003d 0. Here, the discriminant and d are units. It turns out that w1 is (3 + 1) divided by (2 * 2) or 1, and w2 is (3 - 1) divided by 2 * 2 or 1/2.

The result of equating the square expression to zero is calculated according to the algorithm:

1. Determining the number of valid decisions.
2. Calculation d \u003d D ^ (1/2).
3. Finding the result in accordance with the formula (-j +/- d) / (2 * i).
4. Substitution of the result into the original equality for verification.

Some special cases

Depending on the coefficients, the solution may be somewhat simplified. Obviously, if the coefficient in front of the variable is equal to zero to the second degree, then linear equality is obtained. When the coefficient before the variable is zero in the first degree, then two options are possible:

1. the polynomial decomposes into a difference of squares with a negative free term;
2. with a positive constant, real solutions cannot be found.

If the free term is zero, then the roots will be (0; -j)

But there are other special cases that simplify finding a solution.

The reduced equation of the second degree

Referred to as such a square trinomial, where the coefficient in front of the senior term is one. For this situation, the Vieta theorem is applicable, stating that the sum of the roots is equal to the coefficient for the variable in the first degree, multiplied by -1, and the product corresponds to the constant “k”.

Therefore, w1 + w2 equals -j and w1 * w2 equals k if the first coefficient is one. To verify the correctness of such a representation, we can express w2 \u003d -j - w1 from the first formula and substitute it into the second equality w1 * (-j - w1) \u003d k. As a result, the initial equality w1 ^ 2 + j * w1 + k \u003d 0 is obtained.

It is important to notethat i * w ^ 2 + j * w + k \u003d 0 can be reduced by dividing by “i”. The result will be: w ^ 2 + j1 * w + k1 \u003d 0, where j1 is j / i and k1 is k / i.

Take a look at the already solved 2 * w ^ 2 - 3 * w + 1 \u003d 0 with the results w1 \u003d 1 and w2 \u003d 1/2. It is necessary to divide it in half, as a result w ^ 2 - 3/2 * w + 1/2 \u003d 0. Let us verify that the conditions of the theorem are valid for the results found: 1 + 1/2 \u003d 3/2 and 1 * 1/2 \u003d 1 / 2.

Even second multiplier

If the factor of a variable in the first degree (j) is divisible by 2, then we can simplify the formula and look for a solution in a quarter of the discriminant D / 4 \u003d (j / 2) ^ 2 - i * k. it turns out w \u003d (-j +/- d / 2) / i, where d / 2 \u003d D / 4 to the power of 1/2.

If i \u003d 1, and the coefficient j is even, then the solution will be the product of -1 and half of the coefficient for the variable w, plus / minus the root of the square of this half minus the constant “k”. Formula: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.

Higher Discriminant Order

The discriminant of the trinomial of the second degree considered above is the most used particular case. In the general case, the discriminant of a polynomial is multiplied squares of the differences of the roots of this polynomial. Therefore, a discriminant equal to zero indicates the presence of at least two multiple solutions.

Consider i * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0.

D \u003d j ^ 2 * k ^ 2 - 4 * i * k ^ 3 - 4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Let's say the discriminant is greater than zero. This means that there are three roots in the field of real numbers. At zero there are multiple solutions. If D< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.

Video

Our video will talk in detail about the calculation of the discriminant.

Didn't get an answer to your question? Suggest a topic to the authors.

Important! In roots of even multiplicity, the function does not change the sign.

Note! Any nonlinear inequality in the school course of algebra must be solved using the interval method.

I offer you a detailed algorithm for solving inequalities by the interval methodfollowing which you can avoid mistakes when solving nonlinear inequalities.

Solving quadratic equations with negative discriminants

As we know,

i 2 = - 1.

However,

(- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1.

Thus, there are at least two values \u200b\u200bof the square root of - 1, namely i   and - i . But maybe there are some other complex numbers whose squares are equal - 1?

To clarify this question, suppose the square of a complex number a + bi equals - 1. Then

(a + bi ) 2 = - 1,

but 2 + 2abi - b 2 = - 1

Two complex numbers are equal if and only if their real parts and the coefficients of the imaginary parts are equal. therefore

{	and 2 - b 2 = - 1 ab = 0 (1)

According to the second equation of system (1), at least one of the numbers but   and b   should be zero. If a b   \u003d 0, then the first equation yields but   2 \u003d - 1. Number but valid and therefore but 2 >   0. Non-negative number but   2 cannot equal a negative number - 1. Therefore, the equality b   \u003d 0 in this case is impossible. It remains to be recognized that but   \u003d 0, but then from the first equation of the system we obtain: - b 2 = - 1,   b   \u003d ± 1.

Therefore, complex numbers whose squares are -1 are only numbers i   and - i , Conditionally, this is written as:

√-1 \u003d ± i .

By similar reasoning, students can make sure that there are exactly two numbers whose squares are equal to a negative number - but . These numbers are √ ai   and -√ ai   . Conditionally, this is written like this:

√- but = ± √ ai .

Under √ a   here we mean the arithmetic, that is, positive, root. For example, √4 \u003d 2, √9 \u003d .3; so

√-4 = + 2i , √-9 \u003d ± 3 i

If earlier, when considering quadratic equations with negative discriminants, we said that such equations have no roots, now it is no longer possible to say that. Quadratic equations with negative discriminants have complex roots. These roots are obtained according to known formulas. Let, for example, be given the equation x 2 + 2x   + 5 \u003d 0; then

x   1,2 \u003d - 1 ± √1 -5 \u003d - 1 ± √-4 \u003d - 1 ± 2 i .

So, this equation has two roots: x 1 = - 1 +2i ,   x 2 = - 1 - 2i . These roots are mutually conjugate. It is interesting to note that their sum is - 2, and the product is 5, so that the Vieta theorem holds.

The concept of a complex number

A complex number is an expression of the form a + ib, where a and b are any real numbers, i is a special number called an imaginary unit. For such expressions, the concepts of equality and the operations of addition and multiplication are introduced as follows:

1. Two complex numbers a + ib and c + id are called equal if and only if
     a \u003d b and c \u003d d.
2. The sum of two complex numbers a + ib and c + id is called the complex number
     a + c + i (b + d).
3. The product of two complex numbers a + ib and c + id is the complex number
     ac - bd + i (ad + bc).

Complex numbers are often denoted by a single letter, for example, z \u003d a + ib. The real number a is called the real part of the complex number z, the real part is denoted a \u003d Re z. The real number b is called the imaginary part of the complex number z, the imaginary part is denoted by b \u003d Im z. Such names are chosen in connection with the following special properties of complex numbers.

We note that arithmetic operations on complex numbers of the form z \u003d a + i · 0 are carried out in exactly the same way as on real numbers. Really,

Consequently, complex numbers of the form a + i · 0 are naturally identified with real numbers. Because of this, complex numbers of this kind are called simply real. So, the set of real numbers is contained in the set of complex numbers. Many complex numbers are indicated. We have established that, namely

Unlike real numbers, numbers of the form 0 + ib are called purely imaginary. Often they simply write bi, for example, 0 + i 3 \u003d 3 i. The purely imaginary number i1 \u003d 1 i \u003d i has an amazing property:
  Thus,

№ 4 .1. In mathematics, a numerical function is a function whose domains of definition and values \u200b\u200bare subsets of numerical sets - usually a set of real numbers or a set of complex numbers.

Function graph

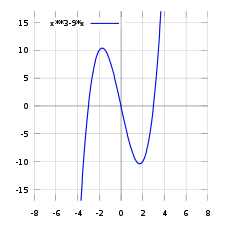
Fragment of function graph

Function Ways

[edit] Analytical method

Usually, a function is defined using a formula that includes variables, operations, and elementary functions. Perhaps a piecewise job, that is, different for different values \u200b\u200bof the argument.

[edit] Tabular way

A function can be defined by listing all its possible arguments and values \u200b\u200bfor them. After that, if necessary, the function can be redefined for arguments that are not in the table by interpolation or extrapolation. Examples include a program guide, train schedule, or a table of values \u200b\u200bfor a Boolean function:

[edit] Graphical way

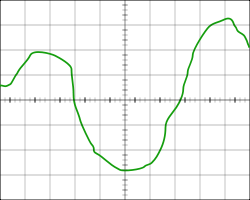
The waveform sets the value of some function graphically.

The function can be set graphically by displaying the many points of its graph on the plane. This can be an approximate sketch of what the function should look like, or readings taken from the device, for example, from an oscilloscope. This method of assignment may suffer from a lack of accuracy, but in some cases other methods of assignment cannot be applied at all. In addition, this method of assigning one of the most representative, convenient for perception and high-quality heuristic analysis of functions.

[edit] Recursive way

A function can be specified recursively, that is, through itself. In this case, some values \u200b\u200bof the function are determined through its other values.

• factorial;
• fibonacci numbers;
• ackerman function.

[edit] Verbal way

The function can be described in words in a natural language in any unambiguous way, for example, by describing its input and output values, or the algorithm by which the function sets the correspondence between these values. Along with the graphical method, sometimes this is the only way to describe a function, although natural languages \u200b\u200bare not as deterministic as formal ones.

• a function that returns a digit in the record of pi by its number;
• a function that returns the number of atoms in the universe at a particular point in time;
• a function that takes a person as an argument and returns the number of people who will be born after his birth