Решение заданий профильного уровня егэ по математике

Задание 1 с решением:

Цена на автобусный билет - 15 рублей.
Сколько билетов можно будет купить на 100 рублей после того, как цена на билет будет повышена на 20%?

Очевидно, что решение данной задачи нужно начинать с нахождения новой цены на билет. То есть той, которая установится после повышения цены на 20%. Найдем новую цену на билет.

1) Находим 20% от 15 рублей. По определению, 1% - это сотая доля. То есть, для того, чтобы найти 20% от 15 рублей, нужно 15 рублей разделить на 100 и умножить на 20. Находим: (15:100)*20=3. Таким образом, 20% от 15 рублей - это 3 рубля.

2) Чтобы найти новую цену - прибавим 3 рубля (равные 20% от 15 рублей) к старой цене билета в 15 рублей. Получаем, что новая цена на билет составит 18 рублей.

3) 100:18=5 (ост 10) - видим, что на 100 рублей можно купить 5 билетов
(и 10 рублей - сдача, которой не хватает еще на один билет по 18 рублей).

Задание 2 с решением:

Дается график, на котором показана температура воздуха в течение трех суток.
На одной оси (абсцисс) отмечается время суток, на другой (ординат) – температура в градусах Цельсия.
Необходимо определить максимальную температуру 15 августа.

Решение:

По условию задачи требуется определить максимальную температуру 15 августа.
На первом этапе выделим 15 августа на графике.

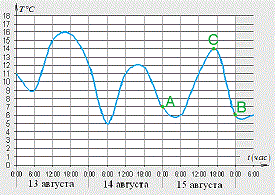
На графике 15 августа мы отметили как AB.
Очевидно, что наибольшей температуре в течение суток соответствует наибольшее значение на промежутке AB.
Это значение мы отметили буквой C. Наибольшая температура за 15 августа 14 градусов Цельсия.

Задание 3 с решением:

Дан четырехугольник, изображенный на клетчатой бумаге. Размер клетки: 1 см х 1 см.
Требуется найти площадь четырехугольника.

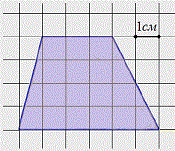
Как и любую новую неизвестную задачу, эту мы сведем к известной.
Очевидно, что на рисунке изображен не просто четырехугольник, а трапеция.
Площадь трапеции вычисляется по формуле:

где h - высота, a, b - верхнее и нижнее основания.
На рисунке видно, что высота трапеции равна 4 см, верхнее основание 3 см, а нижнее 6 см. Тогда по указанной выше формуле находим:

Таким образом, площадь трапеции равна 18 см 2 .

Задание 4 с решением:

Строительная компания должна купить 70 м 3 пеноблоков.
Имеется три поставщика. Условия доставки и цены даны в таблице.
Какая сумма потребуется для самой дешевой покупки с доставкой?

Поставщик	Стоимость пеноблоков (руб. за 1 м 3)	Стоимость доставки (руб.)	Дополнительные условия доставки
1	2600	10000
2	2800	8000	При заказе товара на сумму свыше 150000 рублей доставка бесплатная
3	2700	8000	При заказе товара на сумму свыше 200000 рублей доставка бесплатная

Определим, какую сумму потребуется заплатить каждому из поставщиков.

1 поставщик: 70 * 2600 = 182000, то есть, за 70 м 3 пеноблоков потребуется заплатить 182000 руб.
К этой сумме добавляется стоимость доставки: 182000 + 10000 = 192000 рублей.
Таким образом, первому поставщику нужно будет заплатить 192000 рублей.

2 поставщик: 70 * 2800 = 196000, то есть, за 70 м 3 пеноблоков потребуется заплатить 196000 руб.
В дополнительном условии сказано, что при покупке товара на сумму свыше 150000 рублей доставка бесплатна.
Таким образом, второму поставщику нужно будет заплатить 196000 рублей.

3 поставщик: 70 * 2700 = 189000, то есть, за 70 м 3 пеноблоков потребуется заплатить 189000 руб.
К этой сумме добавляется стоимость доставки: 189000 + 8000 = 197000 рублей.
Таким образом, третьему поставщику нужно будет заплатить 197000 рублей.

Видно, что дешевле всего - купить пеноблоки у первого поставщика и эта покупка обойдется в 192000 рублей.

Ответ: 192000

Задание 5 с решением:

Найти корень уравнения

Решение:

Схема решения этого и подобных ему уравнений проста.
1) Привести левую и правую части уравнения к одному основанию.
2) Решить уравнение, приравняв показатели левой и правой частей уравнения.
В данном случае замечаем, что . Сделаем в исходном уравнении замену:

Тогда по пункту 2) x-2=3. Отсюда получаем, что x = 5.

Задание 6 с решением:

В треугольнике ABC дан угол С, равный 90 градусам, сторона AB равна 5, а косинус угла A равен 0,8.
Требуется найти длину стороны BC.

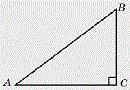
По определению косинус - это отношение прилежащего катета к гипотенузе. То есть, cos A = AC/AB. А значит, 0,8=AC/5.
Отсюда имеем: AC = 4. По теореме Пифагора находим BC: .

Таким образом, ВС=3

Задание 7 с решением:

Найти значение выражения:

Сведение данной задачи к известной можно осуществить с помощью известного свойства логарифмов:

по этой формуле имеем:

Таким образом, значение выражения равно 3.

Задание 8 с решением:

На рисунке дан график функции y=f(x) , а также касательная к графику в точке с абсциссой, равной 3.
Найти значение производной данной функции в точке х = 3 .

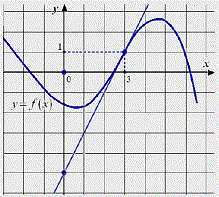
Для решения данной задачи необходимо вспомнить тот факт, что производная функции в точке равна тангенсу угла, образованному касательной и осью Ox. То есть, f"(x o) = tg a.

f"(x o)=tg ACD .

Рассмотрим треугольник ADC и найдем tg ACD. По определению, тангенс равен отношению противолежащего катета к прилежащему. AD=6, CD=3. Отсюда очевидно, что tg ACD = 6/3 = 2. Следовательно, f"(x o) = 2.

Задание 9 с решением:

Площадь боковой поверхности цилиндра равна 16, а диаметр основания - 4.
Найдите высоту цилиндра.

Площадь боковой поверхности цилиндра S бок = 2 rh, где r - радиус основания цилиндра, h - высота цилиндра.
Тогда для нашего случая формулу запишем в виде S бок =dh, где d - диаметр основания цилиндра.
Тогда получим: h = S бок /d. Отсюда получим: h = 16/4

Задание 10 с решением:

Имеется 36 игральных карт. Из колоды наудачу вынимают одну карту.
Какова вероятность, что будет вынута или козырная карта, или туз. Запишите ответ, умноженный на 3.

Пусть событие А заключается в том, что вынута козырная карта, событие
В - вынут "туз". Тогда событие А U B - "вынута или козырная карта, или туз", а событие АВ - "вынут козырной туз". Ясно, что Р(А) = 1/4, p(B) = 4/36,
p(AB) = 1/36, поэтому по формуле
Р(А U В) = 1/4 + 4/36 - 1/36 = 1/3. 1/3 * 3 = 1. Ответ: 1.

Задание 11 с решением:

Дано два цилиндра. Объем первого равен 12 м 3 .
Радиус основания второго в два раза меньше, чем первого, а высота в три раза больше.
Требуется найти объем второго цилиндра.

Объем цилиндра вычисляется по формуле:

Отметим радиус основания первого цилиндра r а высоту h.
Тогда радиус основания второго цилиндра равен r/2 , а высота 3h.
Подставим в указанную выше формулу и получим:

Упростим полученное выражение:

Таким образом, объем второго цилиндра равен 9 м 3 .

Задание 12 с решением:

Камень был подброшен вверх вертикально.
Пока он не упал, высота, на которой находится камень, описывается формулой: h(t) = -5t 2 + 18t
(при этом, h - высота в метрах, а t - время в секундах, которое прошло с момента броска).
Определить, сколько времени камень был на высоте более 9 метров.

Очевидно, что камень может не долететь до отметки 9 метров,
перелететь (и тогда отметку 9 метров он пролетит дважды - когда будет лететь вверх и когда вниз),
либо один раз - если высота его полета составит ровно 9 метров.
Составим и решим уравнение:

В этой статье мы поговорим о сложных заданиях ЕГЭ, о заданиях, представленных во второй части экзамена. О том, как научиться их решать и, по возможности, избежать распространенных ошибок.

Первое задание второй части ЕГЭ по математике (профиль)

Первое из самых сложных заданий ЕГЭ — это уравнение или система уравнений. Они могут быть разных типов:

Логарифмические или показательные
Тригонометрические
Тригонометрические на исследование ОДЗ
Уравнения смешанного типа

Самые частые ошибки — потеря знака, или ошибка в формуле для приведения уравнения к определенному виду. Это, в свою очередь, говорит нам о том, что во-первых нужно быть ОЧЕНЬ внимательным, во-вторых, нужно учить теорию. Если потеря знака приведет к неправильному ответу — баллы все равно будут добавлены, т.к. ход решения был верный. Если же ученик ошибся в формуле, маловероятно, что экзаменатор сжалится — такие ошибки они не любят.

Более подробно о том, как подготовиться к первому заданию, можно .

Второе задание второй части ЕГЭ по математике (профиль)

Это задание на стереометрию. Иногда, считается одним из самых сложных. Чаще всего во варианте нет даже пояснительного рисунка, который бы сэкономил массу времени — приходится чертить самостоятельно. Будьте внимательны при переносе рисунка в чистовик — не перепутайте буквы и обозначайте пунктирами невидимые линии — это могут засчитать как ошибку и снизить баллы.

Чаще всего учащихся подводит незнание какой-либо теории . Им или приходится выводить какую-то необходимую закономерность из более простых тождеств, или расписываться в собственном бессилии.

Более подробно о подготовке ко второму заданию второй части экзамена написано .

Третье задание второй части ЕГЭ по математике (профиль)

В третьем задании второй части учащимся предлагается решить неравенство. Оно может быть одного из следующих типов:

Рациональные неравенства
Иррациональные неравенства
Показательные неравенства
Логарифмические неравенства
Неравенства с логарифмами по переменному основанию
Неравенства с модулем
Смешанные неравенства

Здесь важно понять какой вид неравенства вызывает у вас наибольшие сложности. По опыту специалистов нашего учебного центра, учащиеся допускают наибольшее количество ошибок в неравенствах с модулями. Для того, чтобы подготовиться к третьему заданию второй части ЕГЭ по математике вам необходимо во-первых, выявить ту тему, которая для вас наиболее сложна и отработать ее на более простых неравенствах, во-вторых, научиться решать уравнения под первым номером второй части.

Более подробно о подготовке к третьему заданию .

Четвертое задание второй части ЕГЭ по математике (профиль)

Здесь учащимся предлагается решить планиметрическую задачу. Существенно сложнее той, что дается в шестом задании первой части. Ко всему прочему, иногда в этом задании попадаются задачи на доказательство, что, конечно, знакомо ученикам еще с ОГЭ, но гораздо сложнее. Для более эффективной подготовки нужно, во-первых, выучить теорию, а во-вторых, хорошо и быстро решать задачи под номером шесть в первой части вариантов ЕГЭ.

Более подробно о подготовке к 4 (16) заданию второй части ЕГЭ по математике можно почитать

Пятое задание второй части ЕГЭ по математике (профиль)

Практическая задача. Чаще всего с участием процентов. Для того, чтобы решать такие задачи нужно не только хорошо развитое абстрактное мышление, но и относительно высокий уровень эрудиции, так как при формулировке заданий авторы часто используют весьма специфические экономические термины. Как учиться решать такие задачи? Решать как можно больше. Кстати, вы можете сходить в банк и пообщаться с оператором о вкладе — системы начисления процентов на ваш гипотетический вклад будут не менее сложны, чем те, что описываются в пятом задании второй части ЕГЭ по математике. Вот вам в своем роде бесплатный репетитор по пятому заданию!) Ну и конечно же, наши помогут вам разобраться в тонкостях математики.

Шестое задание второй части ЕГЭ по математике (профиль)

Задача с параметром. Тут может очень повезти, а может не повезти совсем. К сожалению (или к счастью..) «натаскать» на задачу с параметром нельзя, или почти нельзя. Во всяком случае не за год до экзамена. Случаи, конечно, бывают разные, но тем не менее. Как подготовиться — решайте больше. Не знаете как решать — читайте условие, а затем решение. При том, решение вы должны понять, и суметь воспроизвести через, скажем, неделю. Устройте себе подобное испытание, и есть вероятность, что вам на экзамене попадется примерно такая же задача.

Седьмое задание второй части ЕГЭ по математике (профиль)

Задачи на свойства чисел. Для их решения нужно хорошо развитое абстрактное мышление и математическое чутье. Чаще всего для хорошего результата по этому заданию необходима помощь репетитора. Наши дистанционные специалисты занимаются подготовкой ко второй части ЕГЭ по математике и будут рады помочь вам. Первое мини-занятие у нас бесплатно, отправить заявку можно в этой форме:

В данной статье представлен разбор заданий 9-12 части 2 ЕГЭ по математике профильного уровня от репетитора по математике и физике. Видеоурок репетитора с разбором предложенных заданий содержит подробные и понятные комментарии по каждому из них. Если вы только начали подготовку к ЕГЭ по математике, данная статья может оказаться для вас очень полезной.

9. Найдите значение выражения

Используя свойства логарифмов, с которыми вы можете подробно ознакомиться в или в предлагаемом выше видеоуроке, преобразуем выражение:

10. Пружинный маятник совершает колебания с периодом T = 16 с. Масса подвешенного груза m = 0,8 кг. Скорость движения груза изменяется с течение времени в соответствии с формулой

. При этом м/с. Определяющая формула кинетической энергии (в джоулях) имеет вид: , где m берётся в килограммах, — в метрах в секунду. Чему в джоулях равна кинетическая энергия груза через 10 с после начала колебательного движения?

Скорость движения груза через 10 с после начала колебательного движения будет равна:

Тогда кинетическая энергия в этот момент времени будет равна:

Дж.

Пусть x — цена одного леденца, а y — цена шоколадки. Тогда 6 леденцов стоят 6x , а 2% от стоимости шоколадки равны 0,02y . Поскольку известно, что 6 леденцов стоят дешевле шоколадки на 2%, то имеет место первое уравнение: 6x + 0,02y = y , из которого получаем, что x = 0,98/6 y = 98/600 y = 49/300 y . В свою очередь 9 леденцов стоят 9x , то есть 9·49/300 y = 49/300 y = 1,47 y . Задача сводится к тому, чтобы определить на сколько процентов 1,47y больше, чем y . Если y составляет 100%, то 1,47y составляет 1,47·100% = 147%. То есть 1,47y большем, чем y на 47%.

12. Найдите точку минимума функции .

1) ОДЗ задаётся неравенством: title="Rendered by QuickLaTeX.com" height="23" width="106" style="vertical-align: -5px;"> (так выражение, стоящее под знаком логарифма, должно быть больше нуля), откуда получаем, что .

2) Ищем производную функции. Подробный рассказ о том, как вычисляется производная данной функции, смотрите в видео выше. Производная функции равна:

3) Ищем значения x , при которых производная равна 0 или не существует. Она не существует при , так как в этом случае знаменатель обращается в нуль. Производная обнуляется, когда.

ЕГЭ по математике профильный уровень

Работа состоит из 19 заданий.
Часть 1:
8 заданий с кратким ответом базового уровня сложности.
Часть 2:
4 задания с кратким ответом
7 заданий с развернутым ответом высокого уровня сложности.

Время выполнения - 3 часа 55 минут.

Примеры заданий ЕГЭ

Решение задания ЕГЭ по математике.

Задача с решением:

В правильной треугольной пирамиде АВСS с основанием АВС известны ребра: АВ = 5 корней из 3, SC = 13.
Найти угол, образованный плоскостью основания и прямой, проходящей через середину ребер АS и ВС.

Решение:

1. Поскольку SABC - правильная пирамида, то ABC - равносторонний треугольник, а остальные грани - равные между собой равнобедренные треугольники.
То есть все стороны основания равны 5 sqrt(3), а все боковые ребра равны 13.

2. Пусть D - середина BC, E - середина AS, SH - высота, опущенная из точки S к основанию пирамиды, EP - высота, опущенная из точки E к основанию пирамиды.

3. Найдем AD из прямоугольного треугольника CAD по теореме Пифагора. Получится 15/2 = 7.5.

4. Поскольку пирамида правильная, точка H - это точка пересечения высот/медиан/биссектрис треугольника ABC, а значит, делит AD в отношении 2:1 (AH = 2 AD).

5. Найдем SH из прямоугольного треугольника ASH. AH = AD 2/3 = 5, AS = 13, по теореме Пифагора SH = sqrt(13 2 -5 2) = 12.

6. Треугольники AEP и ASH оба прямоугольные и имеют общий угол A, следовательно, подобные. По условию, AE = AS/2, значит, и AP = AH/2, и EP = SH/2.

7. Осталось рассмотреть прямоугольный треугольник EDP (нас как раз интересует угол EDP).
EP = SH/2 = 6;
DP = AD 2/3 = 5;

Тангенс угла EDP = EP/DP = 6/5,
Угол EDP = arctg(6/5)

Ответ:

А знаете ли вы, что?

Среди всех фигур, с одинаковым периметром, у круга будет самая большая площадь. И наоборот, среди всех фигур с одинаковой площадью, у круга будет самый маленький периметр.

Леонардо да Винчи вывел правило, согласно которому квадрат диаметра ствола дерева равен сумме квадратов диаметров ветвей, взятых на общей фиксированной высоте. Более поздние исследования подтвердили его с одним лишь отличием - степень в формуле необязательно равняется 2, а лежит в пределах от 1,8 до 2,3. Традиционно считалось, что эта закономерность объясняется тем, что у дерева с такой структурой оптимальный механизм снабжения веток питательными веществами. Однако в 2010 году американский физик Кристоф Эллой нашёл более простое механическое объяснение феномену: если рассматривать дерево как фрактал, то закон Леонардо минимизирует вероятность слома веток под воздействием ветра.

Лабораторные исследования показали, что пчёлы умеют выбирать оптимальный маршрут. После локализации расставленных в разных местах цветков пчела совершает облёт и возвращается обратно таким образом, что итоговый путь оказывается наикратчайшим. Таким образом, эти насекомые эффективно справляются с классической «задачей коммивояжёра» из информатики, на решение которой современные компьютеры, в зависимости от количества точек, могут тратить не один день.

Если умножить ваш возраст на 7, затем умножить на 1443, то результатом будет ваш возраст написанный три раза подряд.

Мы считаем отрицательные числа чем-то естественным, но так было далеко не всегда. Впервые отрицательные числа были узаконены в Китае в III веке, но использовались лишь для исключительных случаев, так как считались, в общем, бесмыссленными. Чуть позднее отрицательные числа стали использоваться в Индии для обозначения долгов, но западнее они не прижились – знаменитый Диофант Александрийский утверждал, что уравнение 4x+20=0 – абсурдно.

Американский математик Джордж Данциг, будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.

В русской математической литературе ноль не является натуральным числом, а в западной, наоборот, принадлежит ко множеству натуральных чисел.

Используемая нами десятичная система счисления возникла по причине того, что у человека на руках 10 пальцев. Способность к абстрактному счёту появилась у людей не сразу, а использовать для счёта именно пальцы оказалось удобнее всего. Цивилизация майя и независимо от них чукчи исторически использовали двадцатичную систему счисления, применяя пальцы не только рук, но и ног. В основе распространённых в древних Шумере и Вавилоне двенадцатеричной и шестидесятиричной систем тоже было использование рук: большим пальцем отсчитывались фаланги других пальцев ладони, число которых равно 12.

Одна знакомая дама просила Эйнштейна позвонить ей, но предупредила, что номер ее телефона очень сложно запомнить: - 24-361. Запомнили? Повторите! Удивленный Эйнштейн ответил: - Конечно, запомнил! Две дюжины и 19 в квадрате.

Стивен Хокинг - один из крупнейших физиков-теоретиков и популяризатор науки. В рассказе о себе Хокинг упомянул, что стал профессором математики, не получая никакого математического образования со времён средней школы. Когда Хокинг начал преподавать математику в Оксфорде, он читал учебник, опережая собственных студентов на две недели.

Максимальное число, которое можно записать римскими цифрами, не нарушая правил Шварцмана (правил записи римских цифр) - 3999 (MMMCMXCIX) - больше трех цифр подряд писать нельзя.

Известно много притч о том, как один человек предлагает другому расплатиться с ним за некоторую услугу следующим образом: на первую клетку шахматной доски тот положит одно рисовое зёрнышко, на вторую - два и так далее: на каждую следующую клетку вдвое больше, чем на предыдущую. В результате тот, кто расплачивается таким образом, непременно разоряется. Это неудивительно: подсчитано, что общий вес риса составит более 460 миллиардов тонн.

Во многих источниках, зачастую с целью ободрения плохо успевающих учеников, встречается утверждение, что Эйнштейн завалил в школе математику или, более того, вообще учился из рук вон плохо по всем предметам. На самом деле всё обстояло не так: Альберт ещё в раннем возрасте начал проявлять талант в математике и знал её далеко за пределами школьной программы.