Geometry studies the properties of bodies and figures, although such a definition is so broad that it is almost meaningless. So, it allows us to consider a jury member as a geometer of any beauty contest, because he judges the “properties of bodies and figures”, although he understands bodies and figures as something other than a geometer. When someone remarks about a line that it is unusually elegant or expressive, even though it is a curve, that is, an object that is really studied in geometry, the statement itself refers more to the field of aesthetics than to mathematics.
Let’s try to clarify what geometry is and define it with the help of such a concept as symmetry. By symmetry, it is customary to understand such a transformation of a figure that leaves the figure unchanged. For example, the letter H is symmetrical about 180 ° rotation. This means that if the letter H is rotated 180 ° (put “upside down”), then it will go into a figure indistinguishable from the letter H in the initial position (of course, provided that the crossbar in the letter H is strictly in the middle). The word "AHA" on the cover of this book has a mirror, or two-sided symmetry: if you put a mirror on it to the right or left, the mirror reflection of the word will be indistinguishable from the original.
Any section of geometry can be defined as the science of the properties of figures that do not change under certain symmetry transformations. For example, Euclidean geometry on a plane is engaged in the study of properties that remain unchanged (invariant) when a figure moves along a plane, rotates, flips, and uniformly compresses and stretches. Affine geometry studies properties that are invariant with respect to the "skewing" of a figure. Projective geometry studies properties that are invariant under projection. Topology deals with properties that remain unchanged when a figure undergoes arbitrarily strong distortions without tearing and gluing, similar to deformations of a figure made of flexible, tensile and durable material.
Although geometric motifs are found in all chapters of our book, in this chapter we have collected tasks in which the geometric aspect has a clear advantage over everyone else. In the selection, preference was given to tasks that, with the proper approach (and “luck”), allow simple and clear solutions. The first task - about cutting cheese - clearly shows how closely intertwined even in the simplest problems of the "sphere of influence" of the most diverse branches of mathematics: it can be considered as a problem in planimetry, stereometry, combinatorics, number theory. In the same problem, it is not difficult to discern the rudiments of calculating finite differences.
“Horses graze in another field”, oddly enough, is a topological task. The method of threads and buttons allows us to reduce it to the problem of points on a simple closed curve. The shape of the closed curve for solving the problem does not have the slightest significance - only the topological properties of the curve are important. We give a solution to the problem for the case when the points are located on a circle, but with the same success, we could take a curve forming the perimeter of a square or triangle.
The following two tasks (“The Unseen Sword” and “Bet on the Pole”) again take us out of the plane into the Euclidean geometry of three-dimensional space. When looking at flight routes, one involuntarily recalls another famous task on paths - the problem of four turtles. On her example, we see that sometimes simple ideas help to avoid the use of incomparably more complex methods of mathematical analysis. The problem of the skillful surveyor Rensome brings us back to the plane and introduces such chapters of Euclidean geometry as the theory of cuts and partitions. Tasks for the division of land belong to the so-called combinatorial geometry of the plane. Miss Euclid's problem of cutting a cube belongs to the combinatorial geometry of space.
The problem of carpet for an annular corridor and its three-dimensional analogue - the problem of a through-drilled sphere - can serve as excellent examples of how a certain quantity, which, it would seem, should change depending on the values \u200b\u200bof other parameters, actually takes only one value. Who could expect that when drilling in a sphere of a through cylindrical channel of a given length, the volume of the remaining part of the sphere with a constant channel length does not depend on the radius of the sphere or on the diameter of the channel? For the first time faced with a theorem about such an amazing constancy, the mathematician will express his amazement and almost certainly say: “Beautiful result!”
What exactly mathematicians mean by calling a theorem or a formula beautiful is not exactly known. The beauty in their understanding is somehow connected with unexpected simplicity, but no matter how difficult it is to explain what the aesthetic attractiveness of the mathematical statement consists in, all mathematicians can distinguish a beautiful theorem or elegant proof with the same ease with which we distinguish a beauty from an ugly woman. Geometry, which studies objects accessible not only to the mind's eye, but also to direct contemplation, is unusually rich in beautiful theorems and proofs. You will find some of them in this chapter.
How to split a cheese head
The cuisine in the restaurant “At Joe” leaves much to be desired, but the choice of cheeses at Joe is excellent.
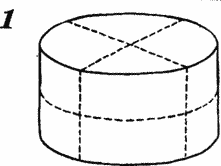
The cylindrical head of cheese is fraught with many interesting cutting tasks. After only 1 straight cut, it is easy to divide it into 2 identical parts.
Two straight sections allow you to divide the head of cheese into 4 identical parts, and 3 straight sections - into 6 equal parts.
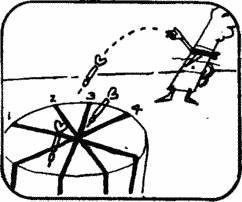
Once, the waitress Rosie asked Joe to cut the cheese into 8 identical parts.
Joe. Good, Rosie. This is not at all difficult to do. I will divide the cheese into 8 identical parts with four straight cuts.
Serving cheese on the table, Rosie suddenly realized that Joe could act more economically: to divide the head into 8 identical parts, it is enough to make only 3 straight cuts.
How to do it?
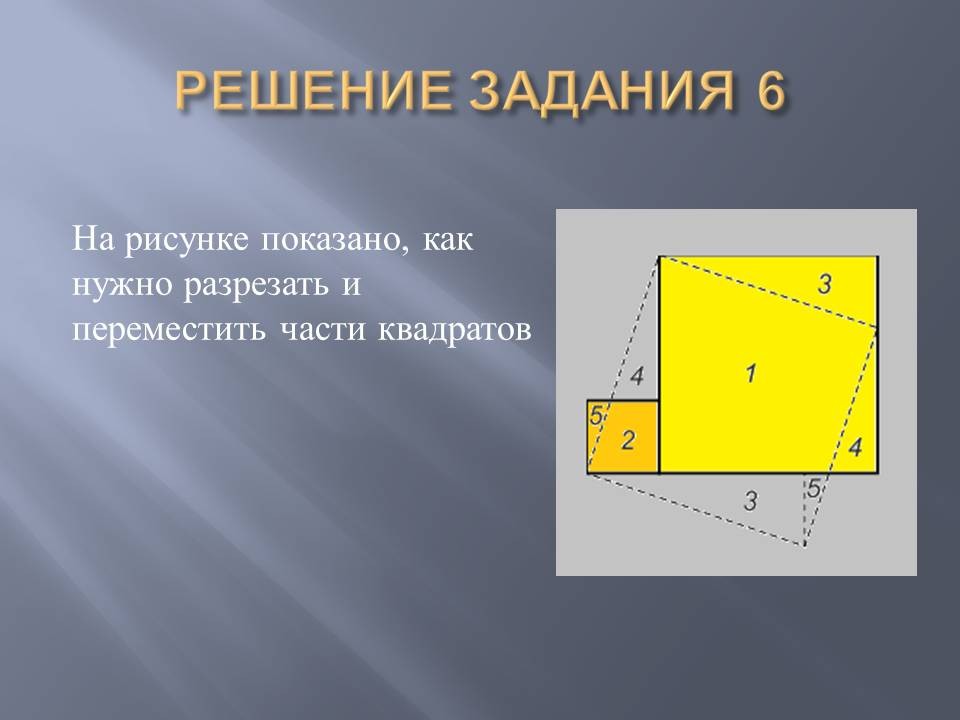
Three cuts?Rosie came up with the idea that the cylindrical head of the cheese is not a flat figure, but a body that can be cut along a horizontal plane passing through its center. In fig. 1 it is shown how to divide cheese into three equal slices into 8 equal servings. This decision assumes that all three cuts are made at the same time. If the cuts are carried out sequentially, one after the other, and before each cut, the pieces of cheese are rearranged in the most convenient way, then with three cuts the cheese can be cut differently (as it was cut ^ on a tray in Rosie's hands): for this, one of two pieces , obtained after the first cut, you need to put on the other, make another cut, take one of the "two-story" halves, put on the other and make the third cut. After the third cut, the cheese head will be divided into 8 equal servings.
Rosie's solution is so simple that it seems almost traumatic, and yet it can serve as a good introduction to a series of important cutting problems, the theory of which is connected with calculating finite differences, and many proofs are carried out by mathematical induction. Finite differences serve as a powerful means of obtaining formulas for the general terms of numerical sequences. The interest in numerical sequences is steadily increasing, which is explained by at least two reasons: firstly, the fact that numerical sequences are found in many numerical problems, and secondly, the speed with which computers allow performing any actions on numerical sequences.
The first method of cutting cheese invented by Rosie (without shifting pieces) consists in making a straight-line or, better, flat cut, passing through the center of the upper base of the cheese, flat, like a round pie. We will find out what numerical sequences can be generated by cutting the upper surface of the cheese with straight lines intersecting in the center (it is clear that n simultaneously conducted cuts allow you to divide the cheese no more than 2 n pieces).
Is it possible to assume that 2 n - the maximum number of parts into which n lines passing through one point, can divide any flat figure bounded by a simple closed curve? No: it is easy to construct a non-convex figure (for example, such as in Fig. 2 ), which one line can be divided into a much larger number of parts. Is it possible to build a figure that can be divided by one straight line into any finite number of congruent parts? If so, what properties should the perimeter of the figure have so that one congruent parts can be cut off from one straight line from it?
The task of cutting a pie or cheese becomes even more interesting when the cut lines do not intersect at one point. It is easy to see that starting si \u003d 3 with this method of cutting, the initial circle will decompose into more than 2 n parts (until we are interested in whether these parts will be congruent or equal). In fig. 3 it is shown how the maximum number of parts is achieved with the number of cuts nequal to 1, 2, 3 and 4 (the circle is divided into 2, 4, 7 and 11 parts, respectively).
The numbers 2, 4, 7, and 11 form a segment of a known sequence with a common term given by the formula
where n - the number of cuts. Putting n \u003d 0, 1, 2, ..., 9, we get the first ten members of the sequence: 1, 2, 4, 7, 11, 16, 22, 29, 37, 46 .... The first differences are 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., the second differences are 1, 1, 1, 1, 1, 1, 1, 1, 1, .... The constancy of the second differences thoroughly supports our conjecture that the common term of this sequence is quadratic in n.
We are talking about a hunch because the formula obtained using finite differences can turn out to be “limitedly applicable” - to generate only a part of the members of an infinite sequence. The applicability of the formula of “finite difference origin” to all members of a numerical sequence without exception must be proved separately each time. In the case of a round cake, such a proof really exists. It is not difficult to find if to use the method of mathematical induction.
After these remarks, which are purely preliminary in nature, you are armed enough to boldly enter uncharted territory and lay dozens of fascinating routes along it in various directions, many of which lead to unusual numerical sequences, formulas and proofs by mathematical induction. Determine the maximum number of parts into which you can divide:
1) horseshoe pie n straight;
2) a cheese head in the shape of a ball or cylinder n flat cuts;
3) pie n circular cuts carried out with a special knife;
4) a cake baked in the shape of a ring (with a round hole in the middle) n straight;
5) bagel (torus) n flat cuts.
In all these tasks, it is assumed that the cuts are carried out simultaneously. How will the answers change if it will be allowed to conduct the cuts sequentially and to shift the formed pieces after each cut?
Invisible sizes

In the center of the city park is a round playground for games. The magistrate set out to set up a diamond-shaped pool on this site.
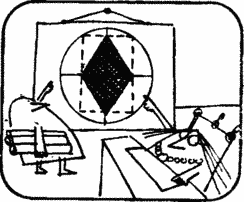
The mayor of the city of Doris Wright, having examined the projects submitted by the architect, expressed her opinion.
Mayor Wright. I like this project of the pool, lined with red tiles. What is the length of each side of the rhombus?
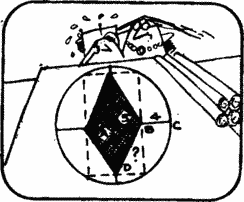
The mayor's question baffled architect Frank Loyd Rong.
Mr. Rong. Now I’ll estimate. Distance from A before B equal to 5 m, and the distance from B before C - 4 m. From these data, you can find the length of the side Bd, for example, calculate it by the Pythagorean theorem.
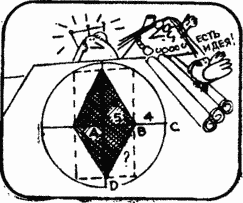
Mr. Rong began calculating, when the venerable Mrs. Wright dawned on him.
Mayor Wright. I have an idea! The length of the side of the pool is exactly 9 m. There is nothing to count here.
Mr. Rong. You are absolutely right!
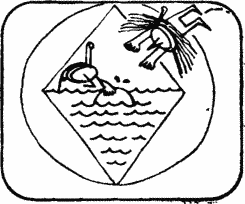
What allowed the mayor and architect to so easily find the length of the side of the pool?
Diagonal and radiusMrs. Wright noticed that each side of the pool coincides with the diagonal of a certain rectangle, the other diagonal of which is equal to the radius of the round playground for games. The diagonals of the rectangle are equal. Therefore, the length of the side of the pool is equal to the radius of the round playground. And since this radius is 5 + 4 \u003d 9 m, then the length of each side of the pool is 9 m. Pythagorean theorem was not needed.
You can better appreciate all the wit of Mrs. Wright's guesses if you try to calculate the length of the side of the pool in a more traditional way. If you want to use only the Pythagorean theorem and the similarity of triangles, then the solution will turn out to be excessively cumbersome. The theorem on intersecting chords, known from planimetry, that the product of the lengths of the segments into which the intersection point divides the chords, the same for all chords intersecting at a given point, allows us to slightly reduce the solution. Using this theorem, you calculate the height of a right-angled triangle (making up a quarter of the basin) equal to v56. Then, by the Pythagorean theorem, knowing two legs, you will find a hypotenuse equal to 9 m.
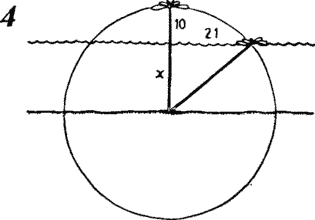
The task of the pool, so gracefully solved by Mrs. Wright, is closely connected with the famous task of water lily, which is found in one of the works of Longfellow. When the stalk of a lily stands upright, its flower 10 cm rises above the surface of the lake. If the lily is pulled to the side, preventing the stem from sagging, then its flower will touch the water at a point 21 cm away from the place where the upright stem came out of the water. What is the depth of the lake where the lily grows?
The Longfellow problem can be easily solved by drawing the diagram shown in Fig. 4 . In essence, this scheme is no different from the pool design presented by architect Rong. It is required to determine the length of the segment x. Like the pool side length problem, the lily problem can be solved in different ways. But if we use the intersecting chord theorem, then the answer is especially easy and fast.
And here is another wonderful task about the pool, difficult to look at, but easily solved if you tell me what its highlight is. Dolphin is at the western edge of the circular pool at A, swims in a straight line 12 m and rests "nose" against the edge of the pool at the point B. Turning, he swims in a straight line in another direction 5 m and again touches the edge of the pool at Cdiametrically opposite point A. What distance would a dolphin have to overcome if he were from a point A swam right to the point C?
The dolphin problem is solved easily and simply by using the theorem that any inscribed angle, based on the diameter of the circle, is a straight line, and notice that the angle Abc just such an angle. Right triangle legs Abc equal to 5 m and 12 m. Therefore, the hypotenuse is 13 m. The moral of all these problems is clear: in many cases, the geometric problem can be solved ridiculously simply if we recall in time the corresponding theorem of Euclidean geometry.
Horses graze on another field
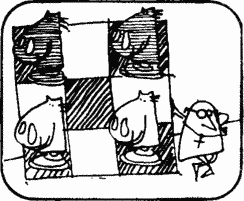
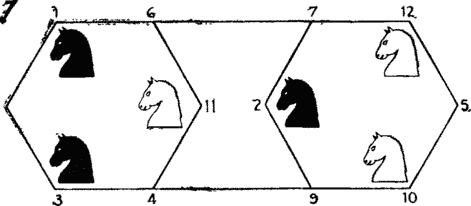
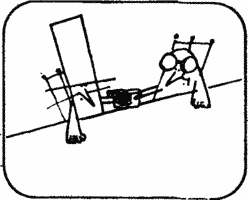
At a chess club meeting, Mr. Bishop proposed the following task.
Mr. Bishop. How to change the positions of black and white horses in the least number of moves?

One of the members of the club made the first 2 moves as shown in the diagram. He managed to rearrange the white knights to the upper corners of the board, and black to the lower corners in 24 moves.

Another member of the club managed to solve the problem of Mr. Bishop in 20 moves.
But no one was able to solve the problem in less than 18 moves, until Fanny Fish appeared.
Miss Fish. I have an idea! I know how to solve a problem in 16 moves, and I can prove that it cannot be solved in fewer moves.
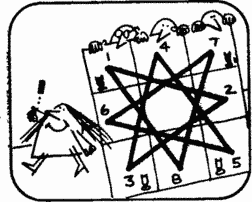
Before proceeding with the explanation, Fanny drew a diagram on which the possible moves of each horse are depicted by line segments.
Miss Fish. Imagine that line segments are threads, and eight cells are strung on them like beads, and they can be arranged around a circle.
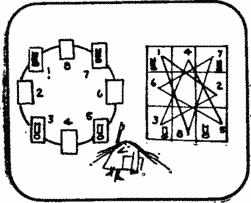
Miss Fish. Each move on the board corresponds to a very specific move on the circle. To change the positions of the horses, they must be moved around the circle, moving in one direction.
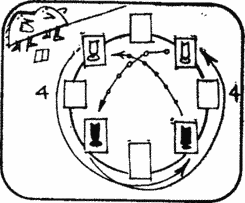
Mr. Bishop. You are absolutely right, Fanny. To move to a new position, each of the 4 horses must make 4 moves. Thus, the problem can be solved in 16 moves, and a more economical solution does not exist.

Fanny replaced one of the white knights with red and asked the members of the chess club a new task: how to swap the white and red knights in the least number of moves?
How do you think why Fanny smiled while offering this puzzle?
Chess horses and star piecesFanny solved the chess problem, reducing it to an isomorphic problem, which allowed a simple (albeit far from trivial!) Solution. The task set by Fanny can be solved by the same method. By combining the threads of the cells occupied by the horses, and turning the resulting "necklace" in a circle, we will see that the horses are strung on the threads in the following order: black, black, red, white. Fanny smiled, because she understood that it was impossible to rearrange the red and white horses: they follow each other in the same order, because no horse can jump over the other horse if they both move in a circle (in any direction) and overtaking is prohibited . Do you understand why?
When moving in a clockwise circle, the white horse always follows immediately after the red one. If the white and red horses could exchange the fields that they occupied on the board from the very beginning, the order would be reversed and the red horse would move in a circle immediately behind the white one. Clearly, such a rebuild is not possible. Indeed, it would mean that one of the horses (either white or red) jumped over two black horses. Having reduced the mini-chess problem to the topological problem of the location of four points on a simple closed curve, we were able to prove very simply that there is no solution to the original problem. Obtaining evidence of “non-existence” in another way would be extremely difficult. Try it and you will see for yourself.
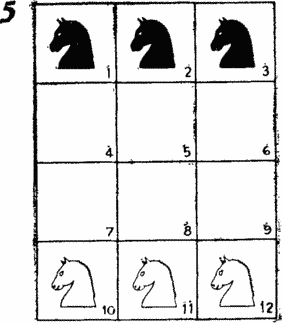
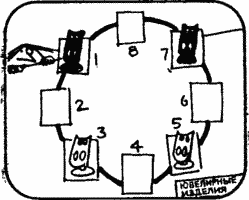
Did you like the task of rearranging chess horses? Here is another such task, in difficulty even surpassing both previous ones. Consider the position on the chessboard 3? 4, shown in Fig. 5 . As before, the three black and three white horses need to be swapped so that the white horses are on the upper horizontal, and the black ones occupy the lower horizontal, and rearrange in the least number of moves.
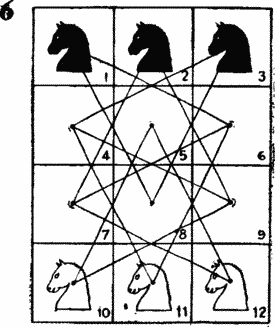
In this case, as can be seen in Fig. 6 , an isomorphic graph is more complicated. This graph is a diagram that shows all the possible moves of the horses. Assuming that the vertices of our graph are buttons or beads and the edges are threads, we find that it is impossible to expand it into a circle, as in the previous task, but our graph from we will be able to lay threads and buttons as shown in fig. 7 . The numbers in this figure correspond to the cell numbers in Fig. 4 and 5 .
It is clear that the problem of rearranging chess horses on this graph is isomorphic to the original problem, but it is solved much easier. Can you find the minimum solution in 18 moves?
The thread and button method allows you to analyze one old game. For her we need a special “board” - the star graph shown in fig. 8 , and seven coins or small chips.
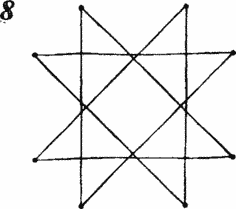
The game is as follows. Putting a coin on any vertex of the graph, you can move it along the black polyline (edges of the graph) to any other vertex. After the move is completed, touching the coin and moving it to another vertex is prohibited.
Then you put the second coin on any unoccupied vertex of the graph and move it along the edges to any other unoccupied vertex. So you continue to act until all seven coins take their place on the top of the graph.
Very soon you will find that you can arrange all seven coins if you act according to a carefully thought-out plan: the slightest negligence leads to a position that does not allow to achieve success in the game. Could you please indicate what rules should be followed when arranging and moving coins so that success will always accompany you?
A star graph can be completely “uncovered” like graphs in the first two problems of rearranging chess horses; it can be turned into a circle. Once this is done, seven coins are easy to place on a circle and analyze how they can move. There are many ways to cope with this task. One of the simplest winning strategies is to make any move with the first coin, and always set and move all of the following coins so that at the end of the move they occupy the top that the previous coin occupied in its original position.
Offer to play this game to your friends. Only very few of them will be able to arrange all seven coins, even if you quickly show them once how to play.
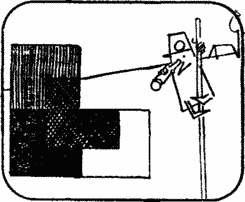
Unprecedented sword
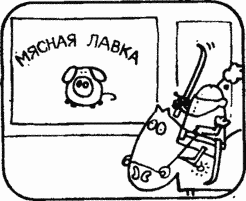
Take a closer look at this picture. What did the artist draw wrong?

Take a look at the sword in the hand of a knight: it cannot be sheathed.
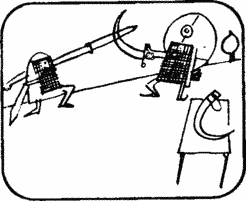
These two swords (unless they have bulges) can be sheathed in an appropriate shape. Can you come up with some other form for the sword and its double scabbard?
Did you get the idea to switch from flat to spatial curves? It turns out that in addition to the two traditional forms of swords that are sheathed, only swords forged in the form of a helix possess the same property.
Irreplaceable curveThe helix plays an important role in modern science, especially in biology and particle physics. DNA molecules are helical. Unlike its one- and two-dimensional cousins \u200b\u200b- straight lines and circles - the helix has "twist", that is, it can be right and left. The straight line and the circle are indistinguishable from their mirror reflections, but to distinguish a helix from its mirror reflection is not the slightest difficulty. In the mirror, the helix, according to Alice from Through the Looking Glass (Lewis Carroll), "is going the other way around."
There are many examples of helix lines in nature and in everyday life. The helix is \u200b\u200btraditionally considered to be right if it twists clockwise as it moves away from you. Screws, bolts and nuts are usually right-cut. Spiral staircases, sugarcane stalks, springs, fibers in ropes and cables and shavings can twist to the right and to the left.
Examples of helix lines found in nature include the horns of many animals, the shells of marine mollusks, the giant narwhal tooth, the human auricle, and the umbilical cord. In the plant world, the helix is \u200b\u200bfound in the structure of stems, shoots, antennae, seeds, flowers, cones, leaves, etc. Climbing to the top of a tree or going down from it, a squirrel describes a helix. Flying out of the cave, bats also move along helical lines. Helical lines wound around a cone can be easily detected in atmospheric phenomena such as whirlwinds or tornadoes. Water flowing in the sink also spins into a funnel woven from helical lines. You will find many other examples of helical lines in the book by M. Gardner, "This Right, Left World."
A regular helix is \u200b\u200ba curve wound on a circular cylinder at a constant angle to the generators (recall that the generators are the straight lines on the surface of the cylinder parallel to its axis). Let be? - the angle at which the helix intersects the generatrices of the cylinder. When? \u003d 0 ° the helix, as it is easy to see, degenerates into a straight line, but at? \u003d 90 ° - in a circle.
Analytically, this can be verified if we write the parametric equations of the helix and measure the angle entering into them? from 0 ° to 90 °. Both the straight line and the circle are the limiting forms of a more general spatial curve, called the helix. A regular helix is \u200b\u200bthe only spatial curve of constant curvature. This explains why scabbard swords can only be made in the form of a regular helix (which would look somewhat unusual) and its two limiting cases - a straight line and a circle.
The projection of a helical line onto a plane perpendicular to its axis has a circle shape. By projecting a helix on a plane parallel to the axis, we get a sine wave. This can be easily verified if we again use the parametric equations of the curve. Many properties of a sinusoid can be studied by its close relative - the helix.
In this regard, we want to tell one funny story-task that admits (with the proper approach) a very simple solution. An elevator runs inside a cylindrical tower 100 meters high. Is there a spiral staircase outside the tower that forms a constant angle with the vertical? \u003d 60 °. The diameter of the tower is 13 m.
Once Mr. and Mrs. Pizza took the elevator to the observation deck, located on the top of the tower. Their son Tomato Pizza chose to go upstairs on foot. When he got to the observation deck, his appearance was not brilliant.
No wonder you're tired, son, ”said Mr. Pizza. “After all, you had to go four times more than us, and all on foot.”
You're wrong, dad, Tom said. - I only went twice more way than you traveled.
Who is right: Tom or his father?
Some people tend to think that in order to calculate the length of a spiral staircase, you need to know the diameter of the tower. In fact, information on the diameter of the tower is completely superfluous!
The fact is that a spiral staircase can be expanded into the hypotenuse of a right-angled triangle with an acute angle of 30 ° and a height of 100 m, and the hypotenuse of such a triangle is twice as high (leg, opposite the angle of 30 °). Therefore, Tom was right.
You can verify this by unrolling a cardboard tube. Perhaps the outcome of the experiment will surprise you a little: you will see that the length of the seam (a helix, as if wound around the tube) does not depend on the diameter of the cylinder into which the right triangle is twisted.
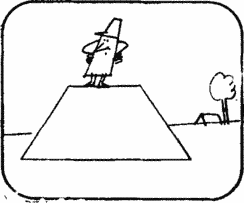
Bet at the Pole
The famous Dan player, nicknamed Bet Bet, was sitting in a bar with his friend Dick, a pilot by profession.
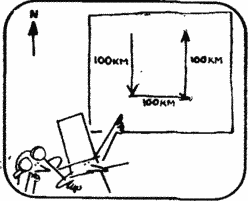
Dan. Dick, I bet a dollar that you can’t solve a simple problem. The plane flies 100 km, heading south, then 100 km east and 100 km north, after which it is at the starting point. Where did he fly from?
Dick. I bet Dan. Your task has long been known. The plane flew from the North Pole.
Dan. Right. Hold the dollar. I bet another dollar that you will never guess where else the plane could have flown from.

Dick was lost in thought.
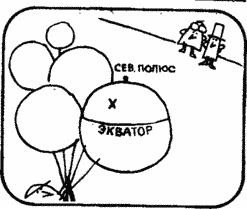
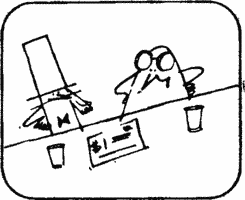
Dick. There is no other point but the North Pole, and it cannot be, and I undertake to prove it. Suppose a plane flies from a point located between the North Pole and the equator.

Dick. It is clear that in this case the end point of the route cannot coincide with the original. If the plane takes off from a point located at the equator, then the end point of the route is approximately 100 km from the starting point.
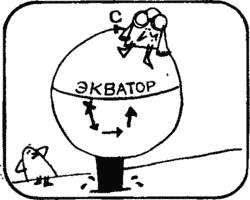
Dick. If the plane takes off from a point located in the southern hemisphere, then the end point will be more than 100 km from the starting point.
Dan. Maybe you want to bet $ 2 that the plane could not fly out of nowhere except the North Pole?
Dick bet and lose. Why?
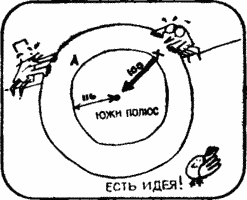
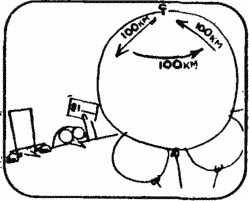
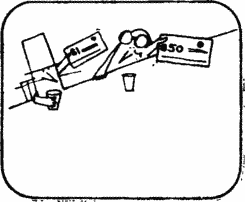
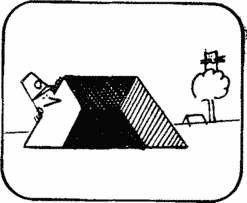
Suppose that the plane started from a point located on parallel A, which is 116 km from the South Pole, and flew 100 km to the south.
Flying 100 km to the east, it will complete a revolution around the South Pole. Having flown then 100 km to the north, he will certainly return to the starting point.
Dick. You're right, here are your 2 dollars.
Dan. I bet another dollar that, in your opinion, I will not be able to indicate other places on the globe, flying from where and flying first 100 km to the south, then 100 km to the east and 100 km to the north, the plane will be able to return to its starting point. By “other places” I mean points that do not lie on parallel A and do not coincide with the North Pole.
Dick. Then I put $ 50, that there are no such points on the globe.
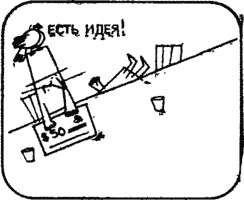
Poor Dick lost again. What important idea did he lose sight of?
Where to fly from?Concluding the second bet, Dick lost sight of a very important circumstance: the point from where the plane flies out can be chosen so close to the South Pole that, having flown 100 km to the east, he will describe not one revolution around the pole, as in the previous solution, but two full turnover. So a new parallel arises, all points of which serve as solutions to the original problem. Similarly, an airplane can fly out from any point on an even smaller circle and, heading east, make three, four, etc. turns around the pole. For any generally positive n you can specify the corresponding parallel, flying from anywhere in which and heading east, the plane will n revolutions around the pole. Therefore, the points from which the plane can fly out, fill in infinitely many parallels, pulled together to the pole,
And here is another navigational task associated with a wonderful curve on the sphere - the loxodrome, or the constant course line. The plane flies from a point located at the equator, and heading to the northeast. Where will his flight end if fuel reserves can be considered unlimited? How long is the route and what does it look like?
You may be surprised to find out that the flight route has the form of a spiral intersecting all meridians at the same angle and ending at the North Pole. It would be more correct to consider such a curve as a helix, wound around a sphere, pulled towards the North Pole and managing to describe infinitely many turns around the pole. If the plane is conventionally taken as a point, then the route, although it manages to make infinitely many revolutions around the pole, has a finite length that can be calculated. Therefore, maintaining a constant speed in flight, the aircraft will reach the North Pole in a finite time.
When applied to a flat map, the shape of the loxodrome is distorted depending on the choice of the cartographic projection. On the Mercator projection, known from the world map, the loxodrome goes straight. That is why the Mercator projection is so widely used in solving navigation problems. If a ship or plane follows a constant course, then to draw it on the map, it is enough to draw a straight line.
And what happens if the plane, taking off from the North Pole, heading southwest? This task is the reverse of the previous one. The flight, as before, will take place at the loxodrome, but we cannot say where the plane will land at the end of the journey. This can be easily verified by turning the clock: no matter where the plane is located on the equator, a plane takes off, moving backwards, it will invariably be at the North Pole. If the plane, having reached the equator, crosses it and will fly the same course, then the loxodrome will be pulled to the South Pole.
When projecting onto a plane tangent to the pole (and parallel to the equatorial plane), the loxodrome goes into an equiangular, or logarithmic, spiral. This spiral crosses the radius vector at a constant angle.
The problem of four bugs is included in the treasury of entertaining mathematics. It is also associated with route building and a logarithmic spiral, but allows an unexpectedly simple solution, eliminating the need for tedious calculations. You will get to know her by reading a short story about the Pizza family and their favorites - four turtles.
Tom Pizza, a trainer and artistic director of turtles, trained his pets so that Abner ( A) always crawled to Bertha, Bertha ( B) - to Charles, Charles ( C) - to Delilah ( D) and Delilah - to Abner. Once he placed the turtles in the corners of the square room so that they formed the tops of the square Abcd, turned on the stopwatch and began to watch what would happen.
It’s interesting, son, ”said Mr. Pizza. - Each turtle crawls straight to its neighbor on the right. All turtles move at the same speed and therefore at any moment of time are at the vertices of a certain square (Fig. 9 ).
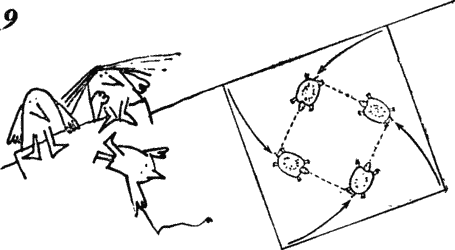
And this square is constantly turning and decreasing, ”added Tom. - Look! You see? Turtles converged in the center!
Suppose that each turtle crawls at a constant speed of 1 cm / s and that the room where they are located has a square shape with a side of 3 m. After how long will the turtles meet in the center of the room? (We arbitrarily take each turtle as a point.)
Mr. Pizza tried to solve the problem by integrating along the trajectory of the turtle, and already pulled out of his pocket a programmable calculator of the latest model, when Mrs. Pizza exclaimed:
No higher math needed, Pepperone! The task is solved very simply! Turtles are found in the center of the room after 5 minutes.
What idea did Mrs. Pizza come up with?
Consider some two turtles located in two adjacent vertices of the square, for example, Abner and Bertu. At every moment, Berta moves at right angles to Abner crawling towards her, since Abner always creeps to Berta, and Berta always creeps to Charles. That is why the turtles are always at the tops of the square. Since Berta never creeps to Abner and does not crawl away from him, her movement does not increase or decrease the distance separating them, and when calculating time, the movement can be neglected. The situation is as if Berta remained in her corner of the room, and Abner crawled towards her along the wall.
This is the key to solving the problem. Abner’s curved path must coincide in length with the side of the initial square, and since this side is 300 cm and Abner crawls at a speed of 1 cm / s, he will crawl to Berta in 300 s, or 5 minutes. The same can be said of all other turtles. Therefore, all turtles are found in the center of the room after 5 minutes.
Using a microcalculator, you can build the trajectories of turtles - curves, described by the vertices of a rotating and simultaneously contracting square, if you put on the diagram successive positions of the vertices at certain intervals. The result of such calculations is presented in Fig. 10 .
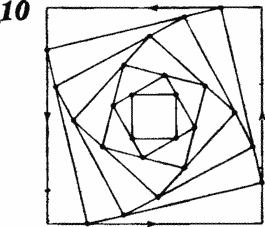
Can you generalize the problem to the case when in the initial position the points are located at the vertices of any regular polygon? Start with an equilateral triangle, then go to the regular pentagon, etc. Can you specify a general formula that allows you to calculate the path length from the known length of the side of the original polygon? What will happen in the extreme case when infinitely many points (turtles) begin to move towards their neighbors on the right (or left) and the vertices of the polygon with an infinite number of sides? Will they ever meet? Now suppose that the original polygons are irregular. What happens, for example, if four turtles take their starting positions at the vertices of a rectangular rather than square room?
Suppose that Tom Pizza turtles after a meeting in the center of the room sprawl, and each of them moves in a straight line from its neighbor to the left? Is it possible to say that the turtles will certainly creep into the corners of the room?
Savings on matches
Once Mabel decided to show prof. Qibble puzzle of matches.
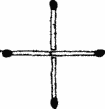
Mabel. You need to build four squares of the same size, moving only 2 matches. Breaking a match, laying them in two or so that they intersect is not allowed.
Prof. Qibble Your puzzle, dear Mabel, has been known for a long time. To solve it, you need to move these 2 matches.
Then prof. Quibble put down 4 matches, after which 12 matches remained on the table.
Prof. Qibble Try to make 6 unit squares of these 12 matches (with a side equal to the length of the match).
No matter how much Mabel fights, solve the puzzle of prof. Quibble she failed. Could you help Mabel?
Match GamesMabel overlooked one important fact: setting the task, prof. Quibble did not say that matches should remain on the plane. If we leave the plane in three-dimensional space, then from 12 matches you can make 12 edges of the cube, which, as you know, has 6 square faces. We see that the key to solving the match puzzle is prof. Quibble is similar to the idea that allowed Rosie to re-cut the head of cheese.
Another variant of the same problem is better known, in which 4 identical equilateral triangles are required to be composed of 6 matches. The solution is to build the frame of the regular tetrahedron from 6 matches.
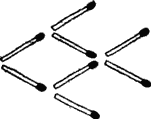
And here are 6 more “match” quick-witted tasks. Will you be able to solve them?
1. After moving as few matches as possible, make a square.
2. Remove as few matches as possible so that the remaining matches form 4 equilateral triangles of the same size as 8 triangles in the initial configuration, and free ends do not stick out anywhere.
3. After moving as few matches as possible, make the fish swim in the opposite direction.
4. After moving as few matches as possible, make the piglet turn in the opposite direction.
5. After moving as few matches as possible, remove the cherry from the glass. An “empty” glass does not have to stand on its stem: it can lie on its side. It is forbidden to move the cherry.
6. With as few matches as possible, remove the olive from the cocktail glass. As in the previous task, an empty glass does not have to stand. It is forbidden to move the olive.
By placing the solutions to these fun puzzles, we would only spoil your pleasure. We only inform you that the first task can be solved by moving 1 match, the second by removing 4 matches, the third, fourth and fifth by moving 3, 2 and 2 matches, respectively, and the sixth by not moving any matches.
Tricky Partitions
Ransom is a land surveyor who specializes in breaking up bizarre sections into congruent parts.
Once he was asked to divide such a site into 4 identical parts. How to do it?
You can divide the plot in the only way - as shown in the figure.
The next time, Ransom needed to divide into 4 congruent parts a section that had the shape of an isosceles trapezoid. This was not easy to do.
However, Ransom did not give in to difficulties and managed to find a unique solution.
Dividing the square section into 4 congruent parts for a specialist like Rance was real fun, but when he was asked to divide the square section into 5 congruent parts, he became stumped.
Ransom. How to do this? After all, there must be some solution ... There is an idea! All clear!
Could you say how Ransom decided to divide the square plot?
Ransom. My method is ridiculously simple and allows you to divide the square into any number of congruent parts.
Cutting tasksIf you want to have fun, invite your friends to solve three of Ransom’s tasks. In the first two tasks, sections in the form of an angle and an equilateral trapezoid can be divided into 4 identical parts - reduced copies of the original section. These decisions indirectly suggest that the square should be divided into 5 parts of a rather bizarre shape, since it cannot be divided into 5 squares.
A simple solution proposed by Ransom comes to mind of very few. It can be proved that a square can be divided into 5 congruent parts only in the way Rance did, and nothing else.
If your friend "gets" in the third task, you will be able to catch him a second time, setting him the fourth task, closely related to the previous one. First of all, show him how the field depicted in Fig. 11 , can be divided into 4 congruent parts, and ask if this field can be divided into 3 congruent parts?
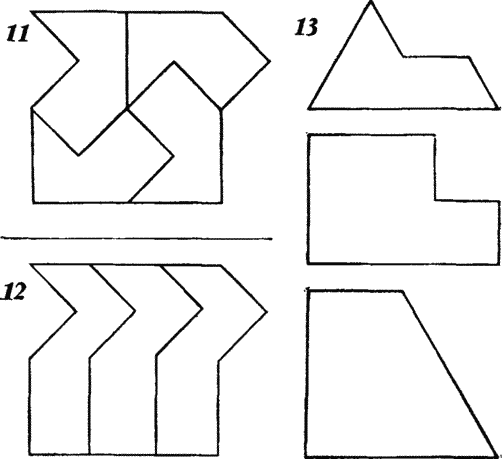
After several attempts, your friend will most likely recognize himself defeated and be sure that he has an unusually difficult task. What will be his surprise when he learns that this problem admits an unexpectedly simple solution, similar to Ransom's proposed partition of the square into 5 congruent parts. This solution is shown in Fig. 12 . As in the case of a square, the method allows splitting the field into any number of congruent parts.
The tasks that land surveyor Rensom and restaurateur Joe have to solve belong to one of the most fascinating sections of entertaining mathematics, sometimes called the theory of partitions. Their unexpected decisions can tell how to deal with many practical problems of geometry on the plane and in space. The first two tasks of Ransom are of particular interest, since in each of them the section is divided into smaller sections, repeating the original in shape. Figures that can be paved without tiles and overlays, like tiles, can be called reduced copies (replicas). rap tiles.
In fig. 13 a few more rap tiles are shown. Can you cut each of them into several congruent parts that repeat the shape of the original figure? We would have an unlimited supply of rep tiles of any shape, from which we could build a non-periodic partition of the plane. For example, consider a L-shaped figure whose rep-tiling was proved by solving the first problem by Ransom. Folded together, four such figures form a new L-shaped figure, which is 4 times larger than the original. Of the four new figures, in turn, an even larger L-shaped figure can be made up. This process can be continued as long as you like and laid out by an L-shaped figure of ever increasing size an infinite plane. For an unlimited time, you can continue not only compiling ever larger L-shaped turnip tiles, but also cutting them into smaller figures.
We know a little about rep tiles. All known pen-tiles, in addition to non-periodic splitting of the plane, also generate periodic splitting of the plane, that is, they allow you to lay out the entire plane so that, subjecting the fundamental region of the pattern only to parallel transfers without turns and reflections, it can cover the entire plane. Is there a rep tile that generates only non-periodic split of the plane? This difficult question of partition theory remains unanswered.
Even less is known about bulky rep tiles. Their number obviously includes a cube, since from 8 cubes you can make 1 larger cube in the same way as from 4 squares you can add 1 bigger square. Can you name any more voluminous rep tiles?
If congruent parts in shape should not repeat the figure made up of them, then the possibilities for inventing puzzle tasks expand. For example, the T-shaped figure in fig. 14 made up of 5 squares. It can’t be cut into four T-shaped pieces, but maybe you can break it into 4 congruent pieces of some other shape?

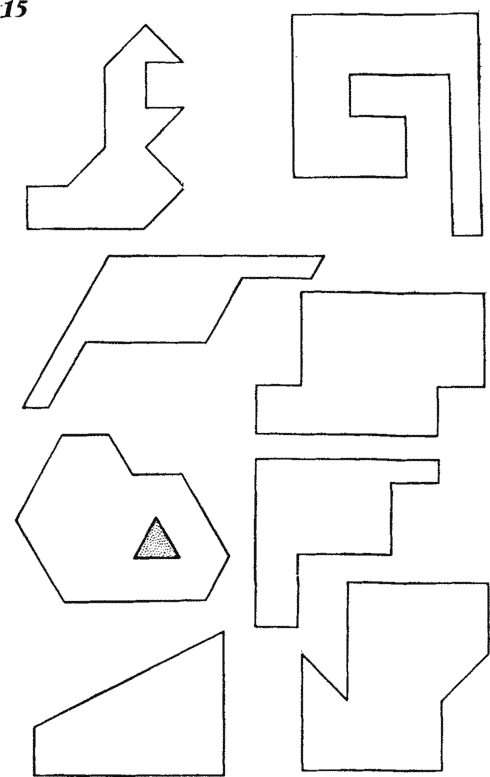
Cutting the plane of the figure even into two congruent parts can be a difficult task. In fig. 15 you see several figures in which you can test the power of your geometric imagination. Solutions (cutting methods) are given at the end of the book.
Another interesting class of cutting problems is formed by cutting tasks of one given polygon into the smallest number of parts of any shape from which another given polygon can be composed. For example, how many parts is enough to cut a square so that they can make an equilateral triangle? (Into 4 parts.) The most complete theory of partitions and the whole range of questions related to cutting is presented in Harry Lindgren's book “Entertaining tasks for cutting”.
Miss Euclid and her cubes
Miss Euclid put a large wooden cube on the chair.
Miss Euclid. Today I will spend with you a control. I will ask you only 3 questions about this cube.
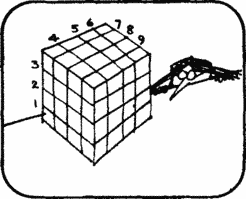
Miss Euclid. This cube can be cut into 64 unit cubes. This requires 9 cuts.
Miss Euclid. If it were allowed to shift parts of the cube before each cut, then it would be possible to limit ourselves to 6 cuts. My first question to you: how to prove that the number of cuts cannot be less than 6?
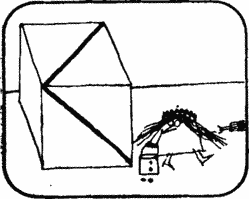
While the class was working on the answer to the first question, Miss Euclid drew on two faces of the cube the diagonals passing through a common vertex.
Miss Euclid. My next question is: what is the angle between these two diagonals?
Before asking her third question, Miss Euclid put a ruler on the top of the cube.
Miss Euclid. How is the easiest way to measure the diagonal length of the cube AB using this ruler?
How many miss Euclid questions could you answer? I was able to answer 2 of 3 questions.
Tricky TasksSolution to Problem 1. Let us prove that it is impossible to cut a 4? 4? 4 cube into 64 cubes with less than 6 flat cuts (provided that after each cut it is allowed to shift parts of the cube). For this, consider any of the 8 inner cubes. None of the inner cubes has “finished” faces that would coincide with the faces of a large cube. Therefore, each of the 6 faces of the inner cube must be selected, which requires 1 flat section. Since no plane can select more than one face of the cube, the number of cuts that must be done to carve all 6 faces of the cube must be at least 6.
Is there a general method that allows you to cut any rectangular box with integer edge lengths into unit cubes with a minimum number of cuts (parts of the box can be rearranged)? Yes, such a method exists and consists in the following. Consider 3 different cubes whose edge lengths are equal to the length, width and height of the box. For each cube, we determine the minimum number of cuts that must be done to divide it into layers of unit thickness. To do this, draw a flat cut perpendicular to the edge of the cube through an integer point located as close as possible to the middle of the edge (if an even number of units fit in the length of the edge, then the cut divides the edge in half; if an odd number of units fit in the length of the edge, then the cut passes at a distance half a unit of length from the middle of the rib), we shift the resulting parts and we will repeat the whole procedure until the whole cube breaks up into layers of unit thickness. The sum of three minima (one for each edge) will give us the answer to the problem.
For example, to cut a rectangular parallelepiped 3 × 4 × 5 into unit cubes, it is necessary to make 7 flat cuts: 2 for the edge 3, 2 for the edge 4 and 3 for the edge 5. The proof of this algorithm was first published in Mathematics Magazine in 1952.
Solution to Problem 2. The problem is solved simply if you realize that on another face of the cube you can draw a third diagonal connecting the ends of the diagonals drawn by Miss Euclid (Fig. 16 ).
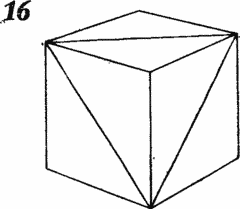
Three diagonals form an equilateral triangle. Since each of the angles of an equilateral triangle is 60 °, the angle between the diagonals drawn by Miss Euclid is 60 °.
Miss Euclid's second task admits an elegant generalization. Suppose that Miss Euclid drew two straight lines connecting the midpoints on the surface of the cube. A, B and C three ribs (Fig. 17 ) What is the angle Abc between these lines?
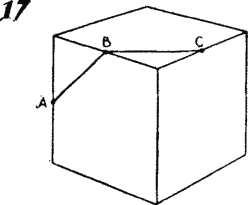
We find the solution of the problem by analogy with the previous solution. First of all, we connect the segments of the straight lines in the middle of the ribs on the other four faces so that all six segments form a closed polygonal line. It is clear that all six segments have the same length and the angles between any two adjacent segments are also the same. Therefore, if we were able to prove that all six vertices of the polygonal line lie in the same plane, then we could argue that our six-link closed polygonal line has the shape of a regular hexagon. It is not difficult to prove the statement we need, but you can verify its validity experimentally by sawing a wooden cube into two halves along a plane passing through the middle of six edges.
The fact that the cross section dividing the cube into two halves may have the shape of a regular hexagon unexpectedly and to some extent contradicts intuition. Well, since we know that the two lines drawn by Miss Euclid are two adjacent sides of a regular hexagon, then it is not difficult to find the angle between them: it is 120 °.
Fig. 17 suggests another interesting problem. Suppose a fly wants to crawl along the surface of a cube from a point A exactly C. Is it possible to consider a path formed by segments Ab and BCthe shortest?
This problem is easily and simply solved by someone who guesses that the shortest path from the point A exactly B on the surface of the cube can be found if two adjacent faces of the cube are expanded so that their planes coincide: the shortest segment is a line connecting the points on the scan A and C. There are two ways to expand two adjacent faces of a cube so that their planes coincide, by choosing either the front and top faces, or the front and right faces, so care must be taken when solving the problem. In the first case, we get a path of length v2, in the second - a path of length v2.5. Therefore, in Fig. 17 the shortest path on the cube surface of A in C.
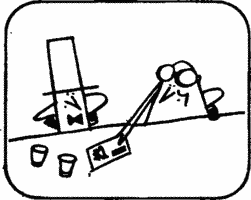
Solution to Problem 3. Of course, the diagonal length of a cube can be determined by measuring the length of the edge with a ruler and applying the Pythagorean theorem twice. But the diagonal of a cube can be measured with a ruler in a much simpler way. Having placed the cube on the edge of the table, we measure the segment equal in length to the edge of the cube, and mark the ends of the segment, after which we move the cube by the length of the edge along the edge of the table (Fig. 18 ) Distance from A before B exactly equal to the diagonal of the cube, and it can be measured with a ruler.

How would you measure the radius of a large ball if you only had a ruler with your hand that was at least one length in length? on the diameter of the ball? One simple way is to stain the ball with soot or lipstick and press it against the wall so that the mark remains on the wall at the point of contact. By measuring the distance from the floor to the mark with a ruler, you determine the radius of the ball. Can you suggest similar methods that allow using some trick to measure the height of a cone or a pyramid? Can you accurately measure the radius of a cylindrical pipe if you have only a carpenter’s square at hand?
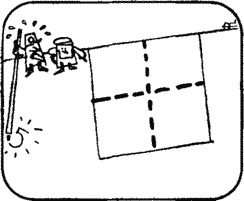
On the carpet
Carpet for the annular corridor in the new airport building was commissioned to produce a company led by Mr. Tech.
Seeing the plan of the corridor, Mr. Taek decided that he made fun of him, I was angry: the only size indicated on the drawing was the length of the chord tangent to the inner wall of the corridor.
Mr. Tack. Remove the drawing so that I no longer see it! How, pray tell, I can submit a quote on the carpet, if I do not know the area of \u200b\u200bthe corridor? I will consult with my designer Mr. Sharp.
Mr. Sharpe, a skilled geometer, listened to Mr. Tek calmly.
Mr. Sharp. The length of this chord, Mr. Taek, is the only size I need. I will substitute it into the formula I know and recognize the area of \u200b\u200bthe corridor.
Mr. Taek looked at Mr. Sharpe for a moment in surprise, and then smiled.
Mr. Tack. Thank you Mr. Sharp, I can tell you the corridor area without it.
Do you know how Mr. Taek managed to determine the area of \u200b\u200bthe ring corridor?
Amazing theoremMr Thack reasoned as follows. Mr. Sharp enjoys a well-deserved reputation as a skilled and knowledgeable geometer, so if he says that he has a formula that allows him to calculate the area of \u200b\u200bthe ring by the length of the chord tangent to the inner circle, then he really has one. If the length of the chord tangent to the inner circle remains equal to 100 m, then no matter how the radii of the outer and inner circles change, according to Mr. Sharp's formula, the area of \u200b\u200bthe ring should remain unchanged.
Then Mr. Taek asked himself what would happen if the radius of the inner ring decreases to zero — its minimum value. The ring in this case will turn into a circle, and a chord 100 m long will become the diameter of the circle. The area of \u200b\u200bthe circle is ? ·fifty? sq. m? 7854 km. m. Therefore, if we assume that the formula of Mr. Sharp exists, then the area of \u200b\u200bthe ring should also be equal to 7854 square meters. m
In the general case, the ring has the same area as a circle with a diameter equal to the length of the largest straight segment that only fits in the ring. This amazing theorem is not difficult to prove if we use the formula for the area of \u200b\u200ba circle.
A three-dimensional analogue of this task is as follows: to find the volume of a segment of a thick-walled cylindrical pipe if, in addition to its length, the length of the longest segment that only fits on one of the pipe ends is known (Fig. 19 ) This segment corresponds to the tangent in the two-dimensional problem, and, knowing its length, we can easily find the cross-sectional area of \u200b\u200bthe pipe. Multiplying the cross-sectional area by the length of the pipe segment, we find its volume.
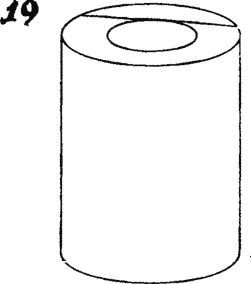
A less obvious three-dimensional analogue of the ring area problem is the following beautiful problem. A through cylindrical hole is drilled through the center of the ball. The length of the channel is 6 cm. What is the volume of the remaining part of the sphere equal to? And in this case it seems that it is impossible to answer the question of the problem: the information that we have is too scarce. However, based on completely elementary considerations, it can be shown that the remaining part of the sphere has the same volume as a solid sphere whose diameter is equal to the length of the drilled channel.
As in the previous case, we get the answer to the problem as soon as we assume that the problem is solvable! Indeed, if a solution to the problem exists, then the volume of the part of the sphere remaining after drilling the through hole should not depend on the diameter of the hole. Let us therefore let the diameter of the hole to the smallest value — zero. The hole is compressed in a straight line - the diameter of the solid sphere. Therefore, the volume of the remaining part of the sphere is 4/3 ? 3? cube cm \u003d 36 ? cube cm.
Cake for the birthday girl

Dinner was coming to an end. Mr. Jones sat at the table with his wife, ten-year-old son, and seven-year-old daughter Susan.
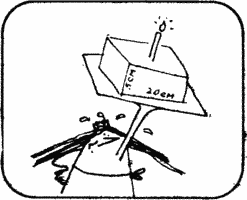
Was Susan's birthday and did Mrs. Jones bake a small square cake of 20 cm? 20 cm and a thickness of 5 cm, abundantly coated with glaze on top and on four sides.
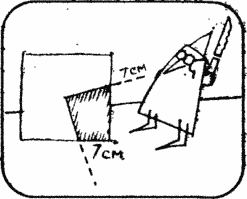
Mr. Jones. Wonderful cake! Enough for everyone. The first piece of cake I will cut for Susan. She is 7 years old today, and I will retreat 7 cm from the corners and draw the cuts through the center.
The piece was bizarre in shape, and Susan, whom he got, complained.
Susan. Dad, you cut me a little piece, less than a quarter! Even if you cut me a quarter of the cake, then the glaze on it is not enough!
Brother Susan had a different opinion.
Mr. Jones. You are both mistaken. Susan received exactly a quarter of the cake and exactly a quarter of the icing.
Could you explain if Mr. Jones is right?
To make sure Mr. Jones is right, it’s enough to continue the cut lines in the center until the intersection with the opposite sides of the cake. By extending each cut, you will immediately be convinced that they divide the cake into four congruent parts.
How to cut a holiday cake?The problem of cutting a pie is easily generalized from a square to other regular polygons.
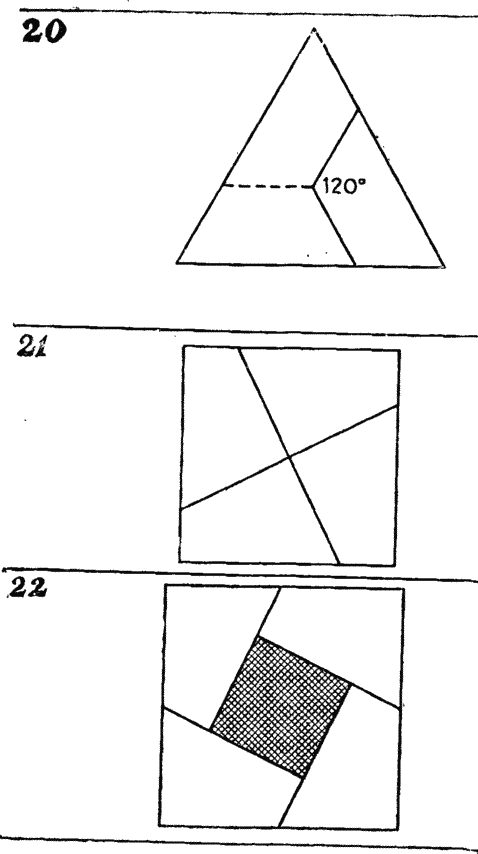
Suppose, for example, that a cake or a holiday cake is baked in the shape of an equilateral triangle and the cuts are made at an angle of 120 ° from the center (Fig. 20 ) It is clear that each piece makes up a third of the pie. This is easy to verify if you draw a dashed line. If the cake is baked in the shape of a regular pentagon, then, having made two cuts from the center at an angle of 72 °, we cut one fifth from the cake. If the cake has the shape of a regular hexagon, then to cut one sixth from it, it is necessary to draw two cuts from the center at an angle of 360 °: 6 \u003d 60 °. The same method is generalized to regular polygons with a large number of sides, although the angle between the cuts is not always expressed as an integer number of degrees.
Cutting a square into 4 congruent parts of another shape has long been one of the favorite cutting tasks. If by cutting a cardboard square into 4 parts as shown in fig. 21 , you suggest to someone from your acquaintances to make a square of quarters, then, as a rule, your friend will find the task difficult. After he successfully copes with it, ask him to make two squares from the same quarters.
The last task, unlike the previous ones, is somewhat fraudulent in nature: your friend will be able to solve it only if it is guessed that one of the two squares is a hole in the middle of the other square (Fig. 22 ) The size of the hole depends on the angle that the cut line is with the side of the original square. If this angle is 90 °, then the hole disappears. If the angle is 45 °, then the hole reaches its largest size.
Notes:
Gardner M. This Right, Left World. - M .: Mir, 1967.
Lindgren G. Entertaining cutting tasks. - M .: Mir, 1977.


















![]()

 Back forward
Back forward
Attention! The slide preview is used for informational purposes only and may not give an idea of \u200b\u200ball the presentation features. If you are interested in this work, please download the full version.
Experience shows that when using practical teaching methods, students are able to form a number of mental devices for students to correctly isolate essential and non-essential features when familiarizing themselves with geometric shapes. developing mathematical intuition, logical and abstract thinking, developing a culture of mathematical speech, developing mathematical and design abilities, increasing cognitive activity, generating cognitive interest, developing intellectual and creative potential. The article presents a number of practical tasks for cutting geometric shapes into parts in order to compose these pieces a new figure. Students work on assignments in groups. Then each group defends its project.
Two figures are called equal if, in a certain way, cutting one of them into a finite number of parts, you can (having located these parts differently) make up a second figure from them. So, the method of partitioning is based on the fact that all sorts of two equally composed polygons are equal in size. It is natural to pose the opposite question: are any two polygons having the same area equal? The answer to this question was given (almost simultaneously) by the Hungarian mathematician Farkas Boyayi (1832) and the German officer and mathematics lover Gervin (1833): two polygons with equal areas are equally spaced.
The Boyayai-Gervin theorem states: any polygon can be cut into parts so that it is possible to add a square from these parts.
Exercise 1.
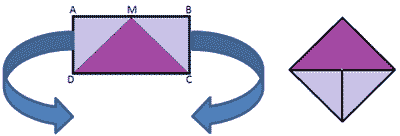
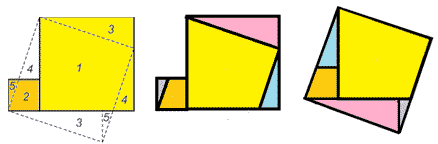
Cut a rectangle ax 2a into parts so that you can make a square out of them.
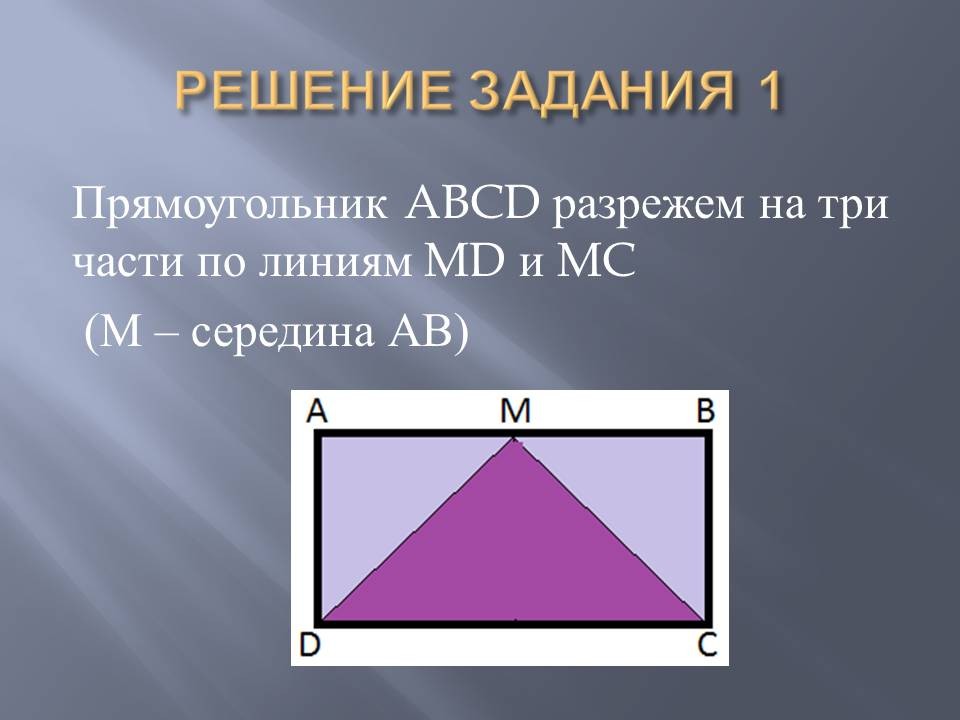
We cut the rectangle ABCD into three parts along the lines MD and MC (M - the middle of AB)
Picture 1
We move the triangle AMD so that the vertex M is aligned with the vertex C, the leg AM will move to the segment DC. Move the MVS triangle to the left and down so that the leg of the MV overlaps half the segment DC. (Picture 1)
Task 2.
Cut an equilateral triangle into pieces so that a square can be folded from them.
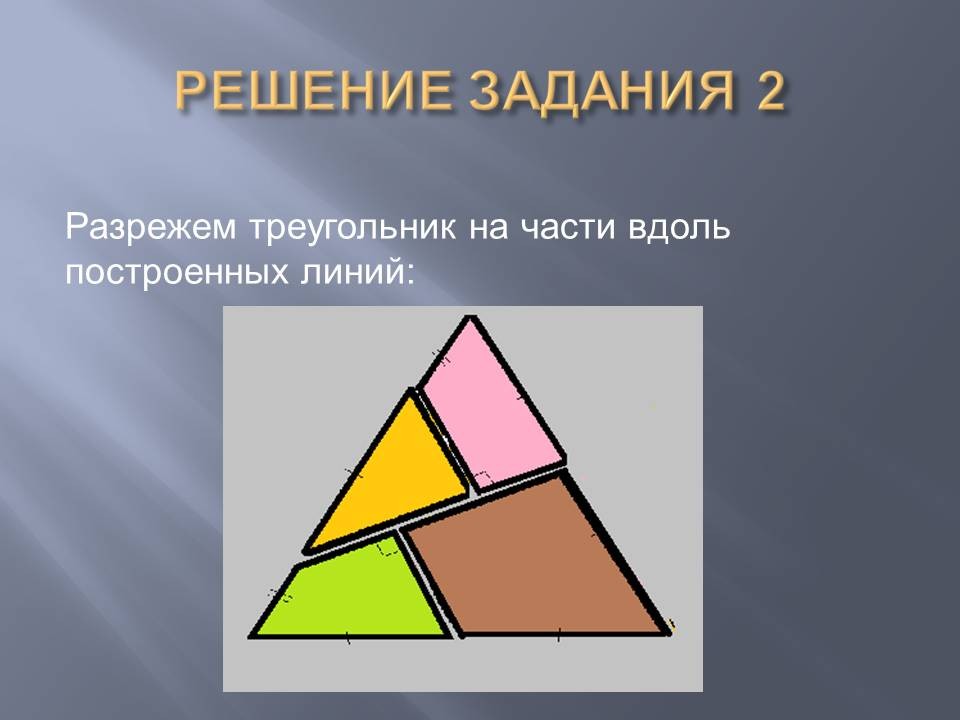
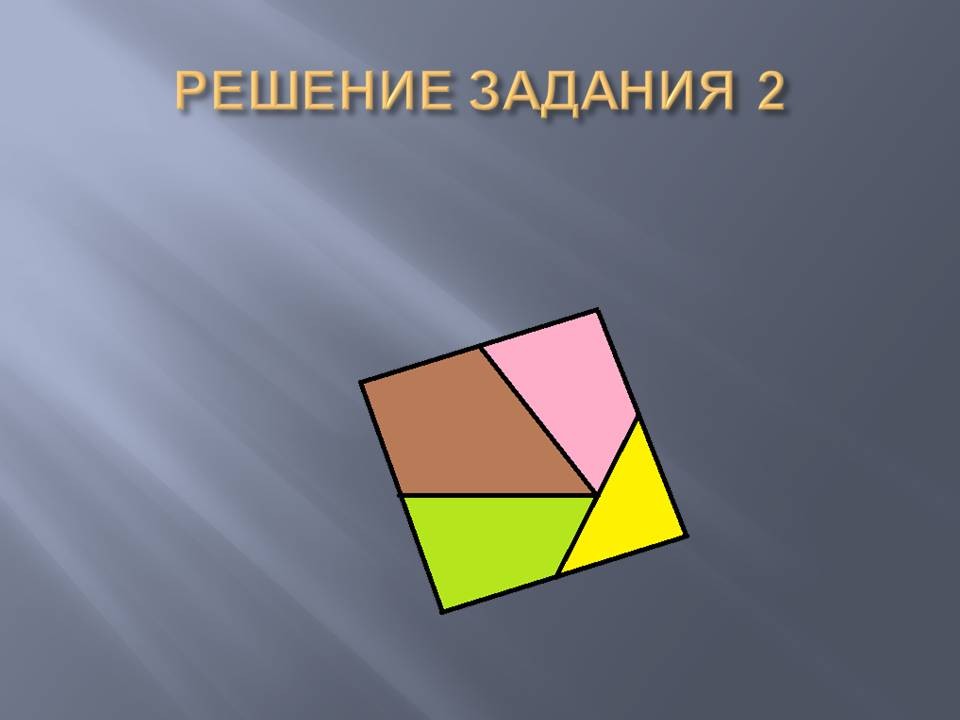
Denote this regular triangle ABC. It is necessary to cut the triangle ABC into polygons so that a square can be folded from them. Then these polygons must have at least one right angle.
Let K be the midpoint of CB, T the middle of AB, let M and E be points on the AC side so that ME \u003d AT \u003d TB \u003d VK \u003d CK \u003d aAM \u003d EC \u003d a/2.
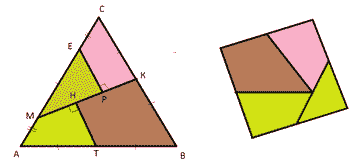
Figure 2
Draw a segment MK and segments perpendicular to it EP and VT. We cut the triangle into pieces along the constructed lines. We rotate the quadrangle CREC clockwise relative to the vertex K so that the SC coincides with the segment KB. We rotate the AMNT quadrangle clockwise relative to the vertex T so that the AT is compatible with the TV. Move the triangle MER so that the result is a square. (Figure 2)
Task 3.
Cut the square into pieces so that two squares can be folded from them.
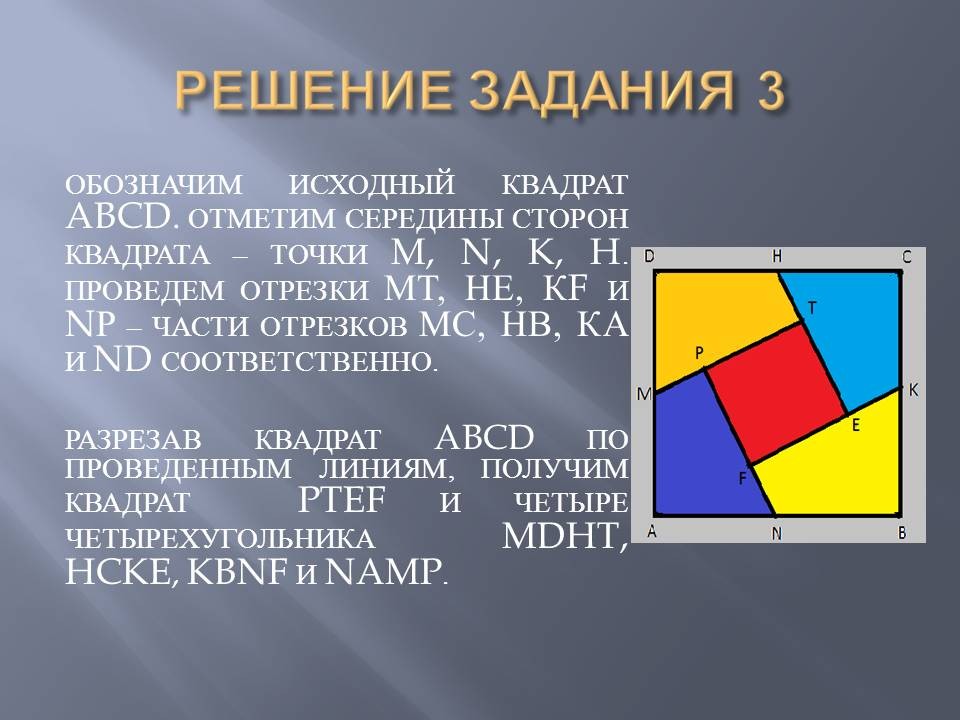
Denote the original square by ABCD. Note the midpoints of the sides of the square — points M, N, K, H. Draw segments MT, HE, KF, and NP — parts of the segments MS, HB, KA, and ND, respectively.
Cutting the square ABCD along the drawn lines, we obtain the PTEF square and four quadrangles MDHT, HCKE, KBNF and NAMP.
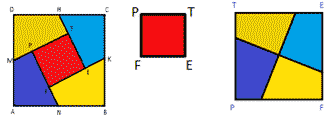
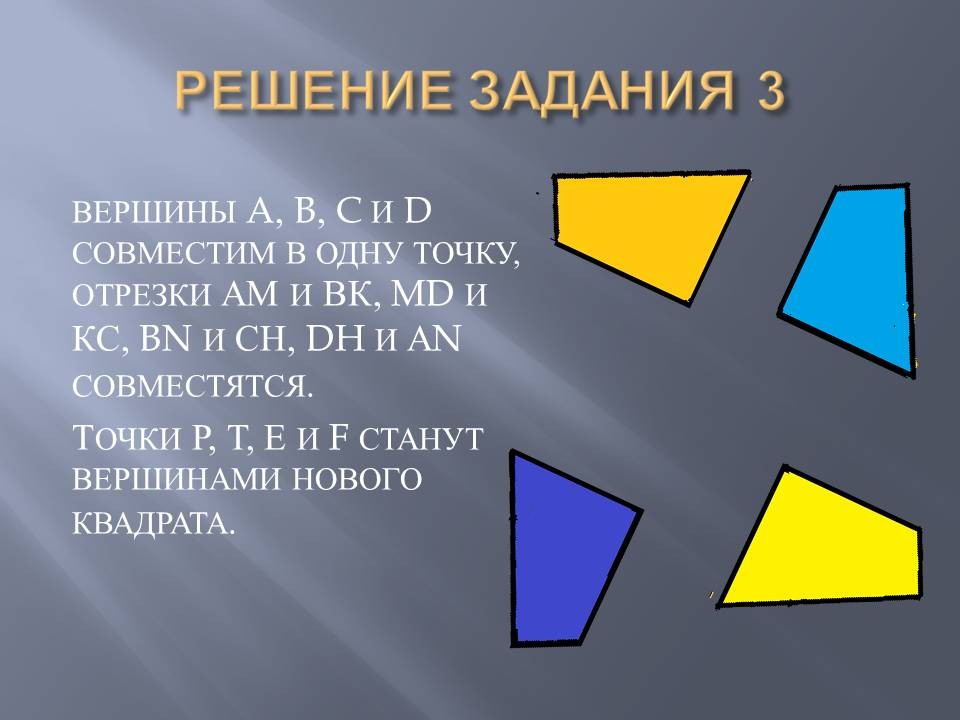
Figure 3
PTEF is a finished square. From the remaining quadrangles, make up the second square. The vertices A, B, C and D are compatible at one point, the segments AM and VK, MD and KS, BN and CH, DH and AN are combined. Points P, T, E and F will become the vertices of the new square. (Figure 3)
Task 4.
An equilateral triangle and square are cut out of thick paper. Cut these shapes into polygons so that one square can be folded from them, while the parts must completely fill it and should not intersect.
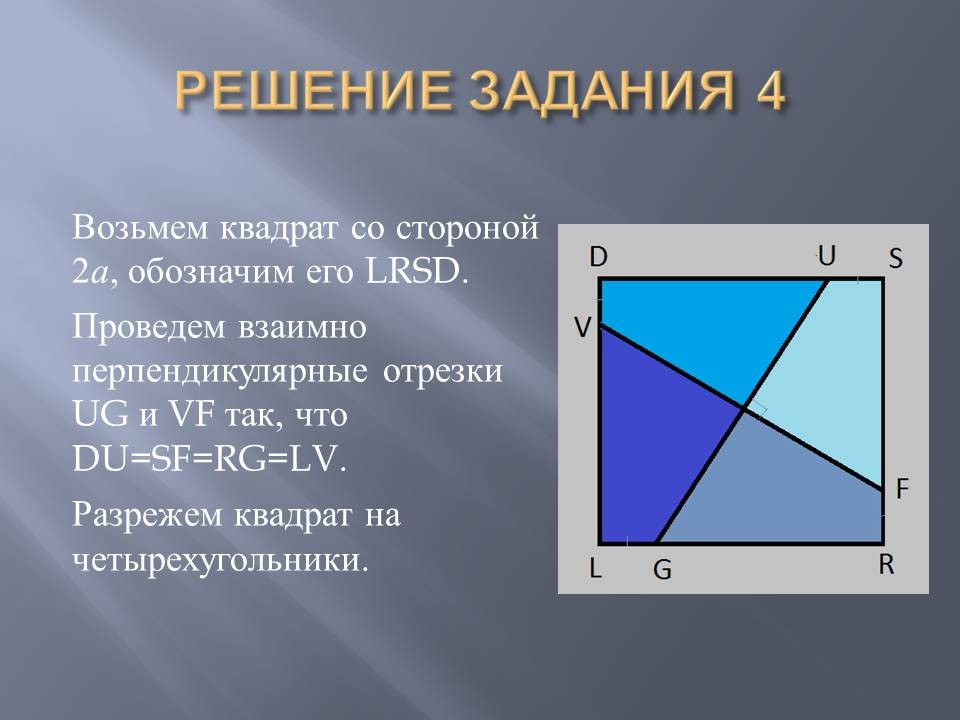
We cut the triangle into parts and make a square out of them, as shown in task 2. The length of the side of the triangle - 2a. Now it is necessary to divide the square into polygons so that from these parts and the square that came out of the triangle, make up a new square. Take a square with side 2 a, denote it by LRSD. We draw mutually perpendicular segments UG and VF so that DU \u003d SF \u003d RG \u003d LV. Cut the square into quadrangles.
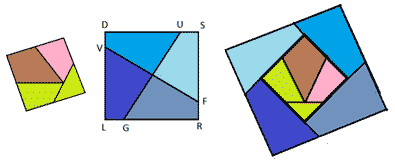
Figure 4
Take a square made up of parts of a triangle. We lay out the quadrangles - the parts of the square as shown in Figure 4.
Task 5.
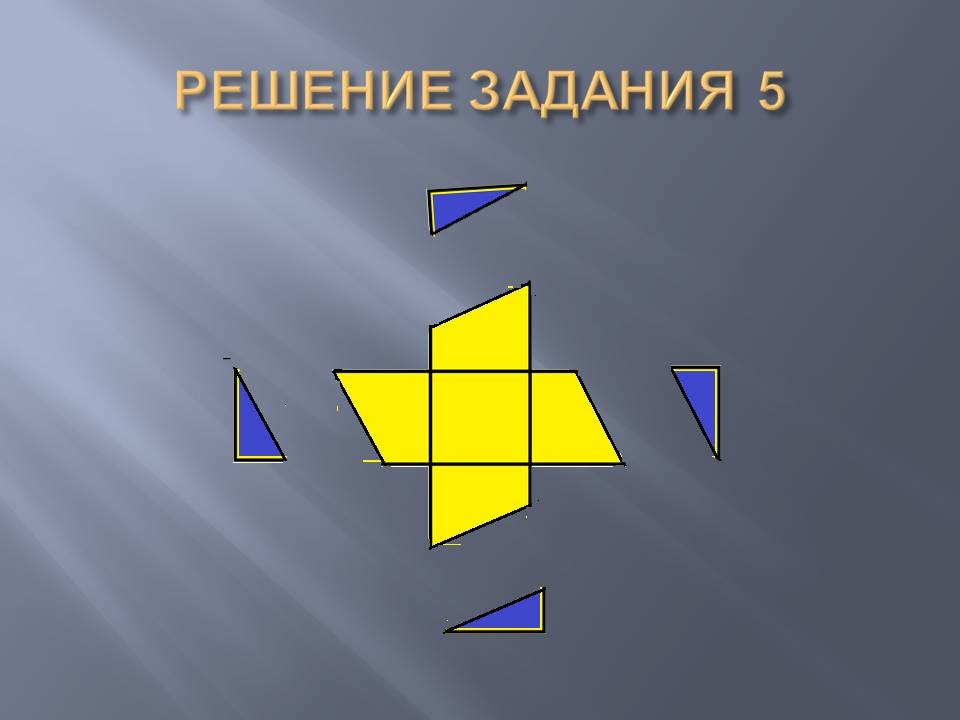
The cross is made up of five squares: one square in the center, and the other four are adjacent to its sides. Cut it into pieces so that you can make a square out of them.
Connect the vertices of the squares as shown in Figure 5. Cut off the “external” triangles and move them to the empty spots inside the ABCS square.
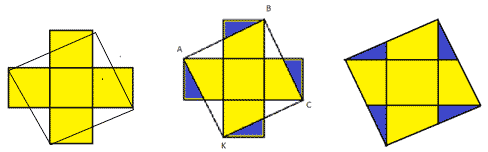
Figure 5
Task 6.
Redraw two arbitrary squares into one.
Figure 6 shows how to cut and move parts of the squares.
In the tutorial of tutors in mathematics and teachers of various electives and circles, a selection of entertaining and developing geometric problems for cutting is proposed. The purpose of using such tasks by the tutor in his classes is not only to interest the student in interesting and effective combinations of cells and figures, but also to form a sense of lines, angles and shapes. The set of tasks is focused mainly on children in grades 4–6, although its use is not ruled out even with high school students. Exercises require students to have a high and adaptive concentration of attention and are great for developing and training visual memory. It is recommended for tutors of mathematics involved in preparing students for entrance exams in mathematical schools and classes, which make special demands on the level of independent thinking and creative abilities of the child. The level of tasks corresponds to the level of introductory Olympiads in the Second School Lyceum (Second Mathematical School), Small Mehmat of Moscow State University, Kurchatov School, etc.
Math tutor note:
In some solutions to problems that you can see by clicking on the corresponding pointer, only one of the possible examples of cutting is indicated. I fully admit that you might get some other correct combination - do not be afraid of this. Check carefully the solution of your mouse and if it meets the condition, then feel free to take on the next task.
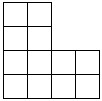
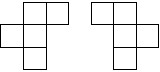
1) Try to cut the figure shown in the figure into 3 parts of equal shape:
: Small shapes are very similar to the letter T
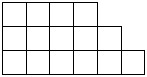
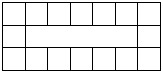
2) Now cut this figure into 4 equally shaped parts:
Math tutorial tip: It is easy to guess that small figures will consist of 3 cells, and there are not many figures of three cells. There are only two of them: a corner and a 1 × 3 rectangle.
3) Cut this figure into 5 equally shaped parts:
Find the number of cells that make up each such shape. These figures are similar to the letter G.
4) And now you need to cut the figure of ten cells into 4 unequal each other rectangle (or square).

Math tutor: Select a rectangle, and then try to enter three more into the remaining cells. If it doesn’t work, then change the first rectangle and try again.
5) The task is complicated: you need to cut the figure into 4 different in form figures (not necessarily rectangles).
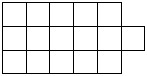
Math tutorial tip: First, draw separately all kinds of shapes of different shapes (there will be more than four) and repeat the method of enumerating options as in the previous task.
:
6) Cut this figure into 5 figures of four cells of different shapes so that in each of them only one green cell is painted over.
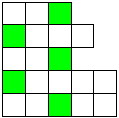
Math tutorial tip: Try to start cutting from the top edge of this shape and you will immediately understand how to proceed.
:
7) Based on the previous task. Find how many total shapes there are of various shapes, consisting of exactly four cells? The figures can be twisted, rotated, but you cannot lift the sable (from its surface) on which it lies. That is, the two figures shown will not be considered equal, since they cannot be obtained from each other by rotation.
Math tutorial tip: Learn the solution to the previous problem and try to imagine the various positions of these figures when turning. It is easy to guess that the answer in our problem is the number 5 or more. (In fact, even more than six). In total there are 7 types of figures described.
8) Cut a square of 16 cells into 4 equally shaped parts so that each of the four parts has exactly one green cell.
Math tutorial tip: The view of the small figures is not a square or a rectangle, or even a corner of four cells. So what figures should you try to cut?
9) Cut the depicted figure into two parts so that a square can be folded from the resulting parts.
Math tutorial: In total, there are 16 cells in the figure, which means that the square will be 4 × 4 in size. And somehow you need to fill in the window in the middle. How to do it? Maybe some kind of shift? Then, since the length of the rectangle is equal to the odd number of cells, cutting must be carried out not in a vertical section, but in a broken line. So that the upper part is cut off on one side of the middle cells, and the lower on the other.
10) Cut a 4 × 9 rectangle into two parts so that you can add a square out of them.
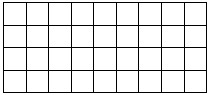
Math tutorial tip: A total of 36 cells in a rectangle. Therefore, the square will be 6 × 6 in size. Since the long side consists of nine cells, three of them must be cut off. How will this cut go further?
11) The cross of five cells, shown in the figure, needs to be cut (the cells themselves can be cut) into parts from which a square could be folded.
Math tutorial tip: It is clear that no matter how we cut the lines of the cells, we won’t get a square, because there are only 5 cells. This is the only task in which it is allowed to cut off-cell. However, it would still be nice to leave them as a guide. for example, it is worth noting that we somehow need to remove the recesses that we have - namely, in the inner corners of our cross. How to do it? For example, cutting off some protruding triangles from the outer corners of the cross ...


