Fig. 33 Example of completing the task of decomposing the number 7 in three different ways
For independent decomposition of the numbers 6 and 8.
As didactic material, “empty” cards and sets of objects are used that the child can use to complete the task. A sample of the decomposition of objects on the card, see figure 33.
Exercise 3. "List all the ways of decomposing the number 5 (4, 3) into the two smallest numbers."
The exercise is performed orally.
Exercise 4. "Fill in the table."
Fig. 34 Cards tables offered to children for the assignment
For work, children are offered cards-tables, samples of which are given above, and sets of numbers in such a volume that they are enough to fill all the options for cards.
The results of 2-4 exercises are evaluated as follows. If the child performs the decomposition of numbers into the two smallest numbers within the first ten without errors, the teacher fixes a high level of assimilation of educational material. If the child is familiar with all methods of decomposition of at least 6 numbers of the first ten, the teacher fixes the average level of learning material. In the event that children have learned how to decompose less than 6 natural numbers of the top ten, the level of assimilation of educational material is considered low.
Tests to determine the level of mastery
Children computing activities
Tests to identify the level of formation of ideas about the arithmetic operations "addition" and "subtraction"
For children 5-7 years old
Four tests are included in this section to reveal the level of children's ideas about the arithmetic operations “addition” and “subtraction”. The first test is represented by an integrated set of tasks, each of which is aimed at identifying certain knowledge of children on the topic under study. Based on the results of these tasks, the teacher can judge how much the child has realized the meaning of arithmetic. Tests 2 - 4 allow you to determine how much the child has learned the relationship between numbers and signs in arithmetic operations.
Test 1The test includes four tasks with the same didactic material. Cards with arithmetic operations for addition and subtraction are offered as didactic material.
Exercise is used when testing both children of the senior, and preparatory group. At the same time, changes are made only to the didactic material, namely: cards with arithmetic expressions are selected that are more complex in composition than in previous tasks. This becomes possible and necessary due to the fact that each subsequent stage of training involves a gradual increase in the segment of the natural number series, within which children perform arithmetic operations, and master the laws of the formation of a new number.
|
|
|
|
|
|
Fig. 35 Cards with arithmetic expressions
In this case, the child should simply demonstrate the ability to read an arithmetic expression.
Task 2. The child is asked to explain what these arithmetic expressions mean.
In completing this part of the assignment, the preschooler must show that he not only knows how to read arithmetic expressions, but also understands the meaning of each of them. The correct answers include approximately the following: “if you add three more objects to three other objects, you get 5 objects”. However, given the possible lack of the necessary skills to express your thoughts, you can offer the following tasks (third and fourth) that will help you determine how much the child understands the meaning of arithmetic.
Task 3. The teacher selects two from the proposed arithmetic expressions: one for addition and one for subtraction and offers the child using toys (several sets of small toys are offered, for example, nesting dolls and bunnies) to demonstrate these actions. Toys should be used in two types, and the number of each type of toy is at least 10 pieces.
Examples of options for the correct execution of the task by the expression 3 + 2 \u003d 5 are given below.
“If we take 3 nesting dolls and add 2 bunnies to them, we get 5 toys.”
“If we take 3 bunnies and add 2 nesting dolls to them, we get 5 toys.”
“If we take 3 bunnies and add 2 more bunnies to them, we get 5 bunnies.”
“If we take 2 nesting dolls and add 3 more nesting dolls to them, we get 5 nesting dolls.”
Thus, when using two sets of dissimilar objects, four answers can be made to this question. During testing, the teacher should encourage the child to find different answers by asking them the question: how else can this arithmetic action be compiled with the proposed toys?
Task 4. The teacher selects two more options from the proposed cards (one for addition, another for subtraction) and offers to draw up arithmetic problems on them.
When working with children of a school preparatory group, the tests below are also used. They are held both at the beginning of the school year and at the end. Changes are made only to the didactic material used during testing (at the end of the school year, large numbers are taken). In this case, all tasks for the tests remain the same.
Test 2 "Compose an arithmetic operation." The teacher asks the children from the numbers 5, 2 and 3 to make an arithmetic action on the subtraction. He asks the question: “How many such actions can be composed”?
Test 3 "Make the inverse arithmetic expression"
Example: 10 - 5 \u003d 5 5 + 5 \u003d 10
For independent work: 5 - 3 \u003d 2
Test 4. "Match the arithmetic action to the scheme. "
Different schemes are presented to the children in turn for arithmetic problems of addition and subtraction (see the figure below).
The child must make a condition and a question that correspond to this scheme, and then, using numbers and arithmetic signs, lay out the action to solve the problem.

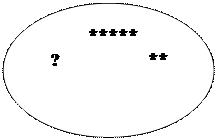
Fig. 36 Schemes for arithmetic problems of addition and subtraction
Note. When testing, the teacher uses only those types of schemes with which children are familiar from the learning process.
Lesson topic:"Factorization of numbers."
The purpose of the lesson: develop the skill of decomposing numbers into prime factors, repeat the signs of divisibility of numbers and use them when decomposing numbers into prime factors, continue to expand students' ideas about the world around them.
DURING THE CLASSES
Teacher: Good afternoon guys. Sit down. Open notebooks and write down the number, cool work. The theme of our lesson is “Factorization of numbers.”
Let's remember what does this mean? Which numbers are prime? What other numbers do you know? Which group does the number 1 belong to? Now we will repeat, we studied, the signs of divisibility of numbers by 3, 9, 5, 2 and 10. (Frontally)
1) Work in pairs. Student assignment: fill out the table:
"W" 312 "h" 310
"E" 567 "in" 585
"S" 555 "b" 771
Answer:
Historical background: Pafnutiy Lvovich Chebyshev - Russian mathematician. He studied the properties of primes. He proved that between any positive integer greater than 1 and twice the number, there is always at least one prime. Let's check this with a few numbers. (Orally)
2) Student Assignment: Connect equal expressions with arrows, first decomposing the numbers from the left column into prime factors.
On the board is written:
125 2 . 2 . 2 . 2 . 7
315 5 . 5 . 5
444 2 . 2 . 3 . 13
112 2 . 2 . 3 . 37
156 3 . 3 . 5 . 7
How else can I write the expressions in the right column?
24 . 7, 53, 22 . 3 . 13, 22 . 3 . 37, 32 . 5 . 7.
2) Check the correctness of the decomposition of numbers into prime factors by putting the signs “+” or “-”.
3) Assignment to students: from the numbers 84, 44, 75, 60, select the one that is decomposed into the largest number of simple factors. Underline this number in green.
4) Work in groups
Assignment to students: from the decompositions of numbers, determine which of them are divided into 2, 3, 4, 6, 7:
- 2 . 11 . 13
- 2 . 5 . 3 . 17
- 3 . 5 . 23 . 41
- 2 . 2 . 2 . 3 . 7.
Write down separately the decompositions of numbers divisible by: by the number 4; by the number 6.
5) When answering questions, write the correct words and in the highlighted column you will receive the name of the scientist, mathematician, who lived before our era.
1. Continue the sentence: a natural number having only two divisors is called ...
2. What is the natural number called by which the number a is divisible without remainder?
3. What number is a divisor of any natural number?
4. Name the author of the first math textbook.
5. Continue the sentence: a natural number with more than two divisors is called ...
6. What are the numbers used in the calculation?
Answers:
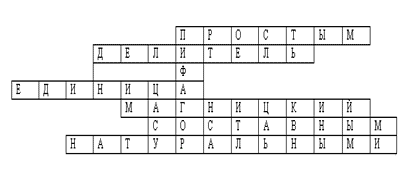
In this crossword puzzle the name of Pythagoras of Samos (“VI century BC) is“ hidden ”. Historical background on this subject: Pythagoras and his students studied the issues of divisibility of numbers. A number equal to the sum of all its divisors (without the number itself), they called the perfect number. For example, 6 \u003d 1 + 2 + 3; 28 \u003d 1 + 2 + 4 + 7 + 14; 496; 8 128.
Lesson summary: Let's summarize a little. What was the purpose of the lesson? Have we reached it?
Homework: paragraph 41, No. 495 (3), No. 503, No. 507 (2).
Definition Converting a polynomial to the product form of two or more polynomials of nonzero degree is called factoring the polynomial. For example: x2 - a2 \u003d (x - a) (x + a).
Consider various techniques for factoring polynomials.
1) The method of grouping and putting the common factor out of brackets.
When using this method, it is sometimes advisable to apply "artificial" transformations - to break apart individual members into similar terms or introduce mutually annihilating members.
Example 1. Factor the polynomial a2 -2bc + 2ac - ab.
Decision. a2 - 2bc + 2ac - ab \u003d (a2 + 2ac) - (2bc + ab) \u003d
A (a + 2s) –b (2s + a) \u003d (a + 2s) (a - b).
Example 2. Factor the polynomial: x2 - 3x + 2.
x2 - 3x + 2 \u003d x2 - x - 2x + 2 \u003d (x2 - x) ‑- (2x - 2) \u003d x (x - 1) - 2 (x - 1) \u003d (x - 1) (x - 2 )
2) The use of formulas of abbreviated multiplication. Using the shortened multiplication formulas, factoring is often greatly facilitated.
Example 3. Factor the polynomial: 5a5x3 + 5a2x9.
Decision. First, take out the common factor 5a2x3, and then apply the formula for the sum of cubes:
5a5x3 + 5a2 x9 \u003d 5a2x3 (a3 + x6) \u003d 5a2x3 (a3 + (x2) 3) \u003d 5a2x3 (a + x2) (a2 - ax2 + x4).
Example 4. Factor the polynomial P (x) \u003d x3 - 3x - 2.
Decision. P (x) \u003d x3 - 3x - 2 \u003d x3 - x - 2x - 2 \u003d (x3 - x) - (2x + 2) \u003d
X (x2 - 1) - 2 (x + 1) \u003d x (x + 1) (x - 1) - 2 (x + 1) \u003d (x + 1) (x2 - x - 2). Because,
x2 - x - 2 \u003d x2 - x - 1 - 1 \u003d (x2 - 1) - (x + 1) \u003d (x + 1) (x - 1) - (x + 1) \u003d (x + 1) (x - 2)
then P (x) \u003d (x + 1) 2 (x - 2).
Full square highlighting is sometimes useful.
Example 5. Factor x4 + 4.
x4 + 4 \u003d x4 + 4x2 + 4 - 4x2 \u003d (x2 +2) 2 - (2x) 2 \u003d (x2 + 2x + 2) (x2 - 2x + 2).
For factoring, it turned out to be successful to isolate the full square in the expression x4 + 4 \u003d (x2) 2 + 22 (the formula a2 + b2 \u003d (a + b) 2 - 2ab was used.
3) Factorization of the square trinomial.
ax2 + bx + c \u003d a (x - x0) (x - x2); (a ≠ 0, D \u003d b2 - 4ac≥0), where x1 and x2 are the roots of the trinomial ax2 + bx + s.
4) Factorization of the nth degree polynomial with respect to x.
A polynomial of degree n with respect to x has the form
P (x) \u003d aohp + a1xn-1 + ... + an-1x + an,
where a0 ≠ 0, n ≥ 0 is an integer, a0, a1, ..., an are constants (polynomial coefficients), the letter (quantity) x can take any numerical values. The polynomial P (x) is written in the standard form in decreasing powers of x.
Two polynomials P (x) and P1 (x) are considered equal: P (x) \u003d P1 (x), if for all values \u200b\u200bof x they take the same values.
Bezout theorem. When dividing the polynomial Pn (x) by the binomial (x-x0), we obtain the remainder R equal to the value of the polynomial at x \u003d x0, i.e. R \u003d Pn (x0).
Pn (x) \u003d (x - x0) Qn-1 (x) + P (x0).
Corollaries from Bezout's theorem:
1. If Pn (x) is divisible by (x - x0) without remainder, ie R \u003d 0, then x \u003d x0 is the root of the polynomial Pn (x), i.e. Pn (x0) \u003d 0.
2. If x \u003d x0 is the root of the polynomial Pn (x), ie Pn (x0) \u003d 0, then Pn (x) is divisible by (x – x0) without remainder, i.e. Pn (x) \u003d (x - x0) Qn-1 (x)).
Summarizing, we get: Pn (x) \u003d a0 (x - x1) (x - x2) ... (x - xn), where x1, x2, ..., xn are the roots of the polynomial.
Example 6. Factor polynomial
P (x) \u003d (x2 + x + 1) (x2 + x + 2) - 12.
P (x) \u003d (x2 + x + 1) ((x2 + x + 1) + 1) - 12 \u003d (x2 + x + 1) 2 + (x2 + x + 1) - 12.
Let x2 + x + 1 \u003d y. Then we have y2 + y - 12 \u003d (y + 4) (y - 3), since the roots of the trinomial y2 + y - 12 are equal to - 4 and 3. Passing from y to x, we get
P (x) \u003d (x2 + x + 5) (x2 + x - 2). Since the trinomial x2 + x - 2 \u003d (x - 1) (x + 2),
then P (x) \u003d (x - 1) (x + 2) (x2 + x + 5).
We begin the study of methods for transforming equations by discussing how to factor the expressions included in this equation. General representation of the equation f (x) \u003d g (x) as F 1 (x) ċ F 2 (x) ċ ... ċ F n (x) \u003d 0,
where are the expressions F k (x), k \u003d 1, ..., n "Simpler" functions f (x) and g (x)represents an undoubted advance in solving the equation. In fact, a representation of the form (5) allows us to immediately equate the factors F k (x) zero and solve simpler equations. The representation of equation (1) in the form of (5) is sometimes called the factorized form of equation (1) (from the English word “factor” is a factor).
We now list some of the most common methods for factoring polynomials, as the simplest algebraic functions.
1. Bracketing the common factor
In the case when all members of the polynomial have the same common factor, it can be taken out of the bracket, thereby obtaining a decomposition of the polynomial.
x 5 - 2x 3 + x 2.
Each term of this polynomial contains a factor x 2. Put it out of the bracket and get the answer: x 5 - 2x 3 + x 2 \u003d x 2 (x 3 - 2x + 1).
2. The application of the formulas of abbreviated multiplication
Reduction formulas are quite effectively applied when factoring a polynomial. It is useful to remember the following formulas: a 2 - b 2 \u003d (a - b) (a + b), a 3 + b 3 \u003d (a + b) (a 2 - ab + b 2), a 3 - b 3 \u003d ( a - b) (a 2 + ab + b 2), a 4 - b 4 \u003d (a 2 - b 2) (a 2 + b 2) \u003d (a - b) (a + b) (a 2 + b 2), a 5 - b 5 \u003d (a - b) (a 4 + a 3 b + a 2 b 2 + ab 3 + b 4), an - bn \u003d (a - b) (an - 1 + an - 2 b + an - 3 b 2 + an - 4 b 3 + ... + a 2 bn - 3 + abn - 2 + bn - 1), n \u200b\u200b∈ ℤ.
Factor polynomial (x - 2) 4 - (3x + 1) 4.
We decompose the difference of the fourth degrees according to the formula given above: (x - 2) 4 - (3 x + 1) 4 \u003d ((x - 2) 2 - (3 x + 1) 2) ((x - 2) 2 + ( 3 x + 1) 2) \u003d \u003d (x - 2 - 3 x - 1) (x - 2 + 3 x + 1) (x 2 - 4 x + 4 + 9 x 2 + 6 x + 1) \u003d \u003d - (2 x + 3) (4 x - 1) (10 x 2 + 2 x + 5).
3. Application of the selection of the full square
Without exaggeration, we can say that the method of selecting the full square is one of the most effective methods of factorization. Its essence lies in the allocation of a full square and the subsequent application of the formula of the difference of squares. Let us explain the above with an example.
Factor polynomial x 4 + 4x 2 - 1.
We have x 4 + 4 x 2 - 1 \u003d x 4 + 2 ċ 2 ċ x 2 + 4 - 4 - 1 \u003d (x 2 + 2) 2 - 5 \u003d (x 2 + 2 - 5) (x 2 + 2 + 5) .
4. Grouping
The method of grouping terms is usually used in conjunction with other methods of factoring and most often with the method of putting out of brackets. The essence of the method is that all terms of a given polynomial are rearranged in such a way that in each group, possibly after putting the common factor out of the brackets, the same expression would form. This expression can also be bracketed as a common factor for all groups.
5. The method of uncertain coefficients
The essence of the method of indeterminate coefficients is that the form of the factors into which the given polynomial is decomposed is guessed, and the coefficients of these factors (also polynomials) are determined by multiplying the factors and equating the coefficients for the same degrees of the variable.
The theoretical basis of the method is the following statements.
- Two polynomials are equal if and only if their coefficients are equal.
- Any polynomial of the third degree has at least one real root, and therefore it decomposes into the product of a linear and quadratic factor.
- Any fourth-degree polynomial is decomposed into a product of second-degree polynomials.
To prove the second statement, let us recall what a graph of a power function with an odd integer power looks like (§ 2.2.5). Indeed, it follows from its form that the value of the polynomial has different signs for x → + ∞ and x → –∞. Polynomial degree n Is a continuous function, which means that there is at least one point at which the graph of this function crosses the axis Ox.
Factor polynomial 3x 3 - x 2 - 3x + 1.
Since a polynomial of the third degree is decomposed into a product of linear and quadratic factors, we will look for polynomials x - p and ax 2 + bx + c such that equality is true 3x 3 - x 2 - 3x + 1 \u003d (x - p) (ax 2 + bx + c) \u003d ax 3 + (b - ap) x 2 + (c - bp) x - pc.
Equating the coefficients at equal degrees on the left and right sides of this equality, we obtain a system of four equations for determining four unknown coefficients: (a \u003d 3 b - a p \u003d - 1 c - b p \u003d - 3 - p c \u003d 1 Solving this system, we obtain: a \u003d 3, p \u003d –1, b \u003d 2, c \u003d –1.
So the polynomial 3x 3 - x 2 - 3x + 1 Factors: 3x 3 - x 2 - 3x + 1 \u003d (x - 1) (3x 2 + 2x - 1).
6. The root theorem of a polynomial
Factorization of a polynomial can sometimes be carried out if one of its roots is guessed using the rational root theorem proved in § 2.1.4. After the root x \u003d α guessed polynomial P n (x) imagine in the form P n (x) \u003d (x - α) ċ P n - 1 (x)where P n - 1 (x) - a polynomial of degree 1 is less than P n (x).
Factor polynomial x 3 - 5x 2 - 2x + 16.
This polynomial has integer coefficients. By the corollary of the rational root theorem (see § 2.1.4), if an integer is the root of this polynomial, then it is a divisor of 16, that is, if a given polynomial has integer roots, then these can only be numbers ± 1, ± 2 , ± 4, ± 8, ± 16.
By checking, we verify that the number 2 is the root of this polynomial, i.e. x 3 - 5x 2 - 2x + 16 \u003d (x - 2) ċ Q (x)where Q (x) - polynomial of the second degree. Consequently, the original polynomial is factorized, one of which ( x - 2).
7. Decomposition with respect to the parameter
The essence of this method is easiest to understand with an example.
Factor polynomial x 4 - 10x 2 - x + 20.
We transform this polynomial: x 4 - 10x 2 - x + 20 \u003d x 4 - 5 ċ 2x 2 - x + 25 - 5 \u003d 25 - 5 (1 + 2x 2) + x 4 - x
Consider now the polynomial a 2 - a (1 + 2x 2) + x 4 - xwhich at a \u003d 5 matches the data. The resulting polynomial is square; its roots can easily be found by the Vieta theorem: a 2 - a (1 + 2x 2) + x 4 - x \u003d a 2 - a (1 + 2x 2) + x (x 3 - 1) \u003d a 2 - a (1 + 2x 2) + x (x - 1) (x 2 + x + 1). Consequently, a 1 \u003d x (x - 1), a 2 \u003d x 2 + x + 1. Hence, the original polynomial is factorized a 2 - a (1 + 2x 2) + x 4 - x \u003d (a - (x 2 - x)) (a - (x 2 + x + 1)). Let us return to the polynomial given in the condition of the problem, substituting a \u003d 5. We get: x 4 - 10x 2 + x + 20 \u003d (5 - x 2 + x) (5 - x 2 - x - 1) \u003d (x 2 - x - 5) (x 2 + x - 4).


