“The limit of function at a point” is Aspiration. In between. Which they read: “the limit of function. Continuous at a point. Function defined. Point. Functions when striving. Note on. Fairly approximate equality: Function. Differ from the limit value. For sufficiently small values. Continuous at any point, at any. Examples. But when calculating the limit of the function for.
"Point of symmetry" - Symmetry in everyday life. For n \u003d 2, we have axial symmetry. . Axial and central symmetry. Such a figure has central symmetry. Shapes that do not have axes of symmetry. Such a figure has axial symmetry. A parallelogram has only central symmetry. Examples of symmetry of plane figures. Symmetry of flat figures.
“Oscillation of a Point" - Lecture 3: rectilinear vibrations of a material point. Purely forced vibrations. 1. Examples of fluctuations. Heartbeat. The movement is fading and aperiodic. Resonance. Intermediate situation. The coefficient of dynamism. Low resistance. Geometric progression. - Complex conjugate. Great resistance.
“Parallelism of two lines” - Are the lines parallel? Prove that NP || MQ. Prove that AB || CD C is secant for a and b. The relative position of two lines on the plane. Prove that AC || Bd. CD is the angle bisector of ALL. What are the pairs: - crosswise lying corners; - corresponding angles; - one-sided corners; Examples of parallelism in real life.
“Ray is a straight segment” - Direct, Coordinate. Line, Point, Point O - the beginning of the beam. Numbers - coordinates of points: Ray FR. Straight. Points C and D are the ends of the segment of diabetes. Name the segments, lines and rays shown in the figure. Section. Ray PM. The segment OE is the unit segment, OE \u003d 1. Ray. Point. S.
“Two frosts” - And when I got to the place, it got worse for me. Live with me, you will find out that an ax warms better than a fur coat. Elder brother, Frost - Blue nose, chuckles, but pats the mitten on the mitten. Two Frosts, two siblings walked across the open field. Frost shook his head - Blue nose and says: - Uh, you are young, brother, and stupid.
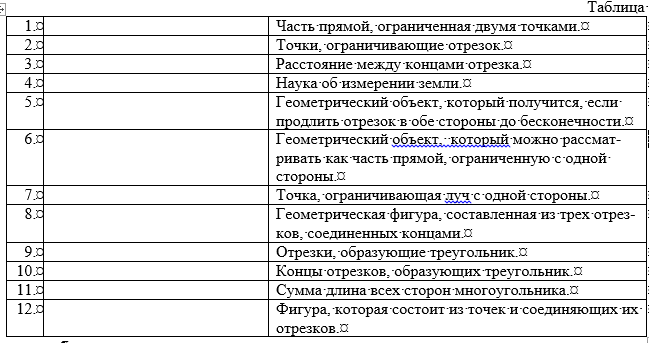
Section. The length of the segment. Triangle.
1. In this section you will get acquainted with some concepts of geometry. Geometry- The science of "measuring the earth." This word comes from Latin words: geo - earth and metr - measure, measure. In geometry, various geometric objects, their properties, their connection with the outside world. The simplest geometric objects are a point, a line, a surface. More complex geometric objects, for example, geometric figures and bodies, are formed from the simplest.
If we attach a ruler to two points A and B and draw a line along it connecting these points, then we get section, which is called AB or VA (we read: "a - be", "be - a"). Points A and B are called cut ends (picture 1). The distance between the ends of the segment, measured in units of length, is called long cutka.
Length units: m - meter, cm - centimeter, dm - decimeter, mm - millimeter, km - kilometer, etc. (1 km \u003d 1000 m; 1m \u003d 10 dm; 1 dm \u003d 10 cm; 1 cm \u003d 10 mm).To measure the length of the segments using a ruler, tape measure. To measure the length of a segment means to find out how many times a particular measure of length fits into it.
Equal called two segments, which can be combined by superimposing one on the other (Figure 2). For example, you can actually or mentally cut one of the segments and attach to the other so that their ends coincide. If the segments AB and SK are equal, then write AB \u003d SK. Equal lengths have equal lengths. The converse is true: two segments having equal lengths are equal. If two segments have different lengths, then they are not equal. Of two unequal segments, the smaller is the one that forms part of the other segment. You can compare line overlays using a compass.

If we mentally extend the segment AB in both directions to infinity, then we get an idea about straight AB (Figure 3). Any point lying on a line splits it into two beam(figure 4). Point C splits line AB into two beam CA and CB. Longing C is called beam start.
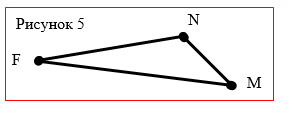
2. If three points that do not lie on one straight line are connected by segments, then we obtain a figure called the triangle.These points are called peaks triangle, and the segments connecting them, the parties triangle (figure 5). FNM - triangle, segments FN, NM, FM - sides of the triangle, points F, N, M - vertices of the triangle. The sides of all triangles have the following property: the line of either side of the triangle is always less than the sum of the lengths of its two other sides.
If we mentally extend in all directions, for example, the surface of the tabletop, we get an idea about the plane. Points, segments, straight lines, rays are located on the plane (Figure 6).

Block 1. Optional
The world in which we live, all that surrounds us, the ancients called nature or space. The space in which we live is considered three-dimensional, i.e. has three dimensions. They are often called: length, width and height (for example, the length of the room is 4 m, the width of the room is 2 m and the height is 3 m).
The idea of \u200b\u200ba geometric (mathematical) point is given to us by a star in the night sky, a point at the end of this sentence, a trace from a needle, etc. However, all of the listed objects have dimensions, in contrast to them, the dimensions of the geometric point are considered equal to zero (its measurements are equal to zero). Therefore, a real mathematical point can only be imagined. You can also say where it is located. Putting a point in a notebook with a pen, we will not depict a geometric point, but we will assume that the constructed object is a geometric point (Figure 6). Dots are denoted in capital letters of the Latin alphabet: A, B, C, D, (read " point a, point be, point ce, point de) (Figure 7).
The wires hanging on the poles, the visible horizon line (the boundary between heaven and earth or water), the riverbed depicted on the map, a gymnastic hoop, a stream of water beating from a fountain give us an idea of \u200b\u200bthe lines.

Distinguish between closed and open lines, smooth and nonsmooth lines, lines with self-intersection and without self-intersection (Figures 8 and 9).

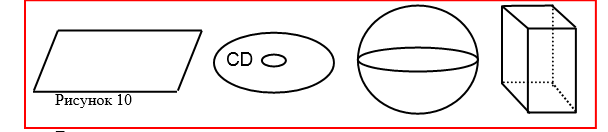
A sheet of paper, a laser disc, a shell of a soccer ball, cardboard packaging box, New Year's plastic mask, etc. give us an idea of surfaces(figure 10). When the floor of a room or a car is painted, it is precisely the surface of the floor or car that is painted.
Human body, stone, brick, cheese head, ball, icicle, etc. give us an idea of geometricbodies (Figure 11).

The simplest of all lines is it's direct. We attach a ruler to a sheet of paper and draw a straight line along it with a pencil. Mentally continuing this line to infinity in both directions, we get an idea of \u200b\u200bthe line. It is believed that the line has one dimension - the length, and its other two dimensions are zero (Figure 12).
When solving problems, the line is depicted in the form of a line, which is drawn along the ruler with a pencil or chalk. Lines are indicated by lowercase Latin letters: a, b, n, m (Figure 13). You can also designate a line with two letters corresponding to the points lying on it. For example, direct n Figure 13 can be designated: AB or VA, AD orDA,DB or BD.

Points can lie on a straight line (belong to a straight line) and not lie on a straight line (not belong to a straight line). Figure 13 shows points A, D, B lying on line AB (belonging to line AB). At the same time they write. Read: point A belongs to line AB, point B belongs to AB, point D belongs to AB. The point D also belongs to the line m; it is called common point. At point D, lines AB and m intersect. Points P and R do not belong to lines AB and m:
Through any two points always you can draw a straight line and only one .
Of all the types of lines connecting any two points, the smallest length is the segment whose ends are given points (Figure 14).
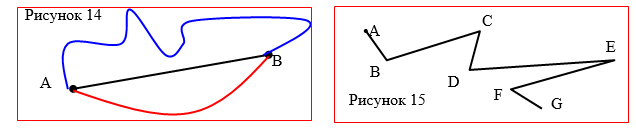
The figure, which consists of points and segments connecting them, is called a broken line. (Figure 15). The segments forming a polyline are called links broken line, and their ends - peaksbroken line. They call (designate) a broken line, listing in order all its vertices, for example, a broken line ABCDEFG. The length of a broken line is the sum of the lengths of its links. Therefore, the length of the broken line ABCDEFG is equal to the sum: AB + BC + CD + DE + EF + FG.
Closed polyline is called polygonits peaks are called polygon verticesand her links the parties polygon (Figure 16). They call (designate) a polygon, listing in order all its vertices, starting from any, for example, a polygon (heptagon) ABCDEFG, a polygon (pentagon) RTPKL:

The sum of the lengths of all sides of the polygon is called perimeter polygon and is indicated by latin the letterp (read: pe) The perimeters of the polygons in Figure 13:
P ABCDEFG \u003d AB + BC + CD + DE + EF + FG + GA.
P RTPKL \u003d RT + TP + PK + KL + LR.
Mentally extending the surface of the table cover or window glass to infinity in all directions, we get an idea of \u200b\u200bthe surface, which is called plane (Figure 17). Designate the plane in small letters of the Greek alphabet: α, β, γ, δ, ... (read: plane alpha, betta, gamma, delta, etc.).
![]()
Block 2. Dictionary.
Compile a dictionary of new terms and definitions from §2. To do this, enter the words from the list of terms below in the empty rows of the table. In table 2, indicate the term numbers according to line numbers. It is recommended that before filling out the dictionary, carefully review §2 and block 2.1 again.

Block 3. Set compliance (CSS).
Geometric figures.
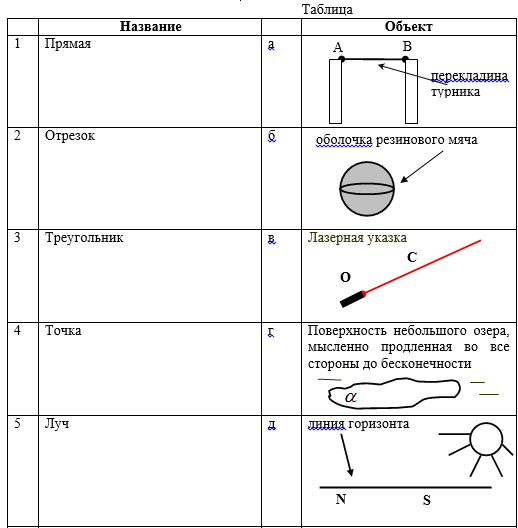

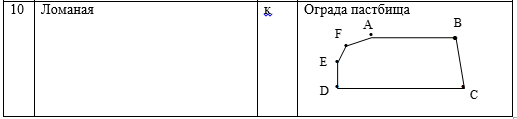
Block 4. Self-test.
Measure a line using a ruler.
Recall that to measure the segment AB in centimeters, then compare it with a segment 1 cm long and find out how many such 1 cm segments fit in the AB segment. To measure the length in other units of length, do the same.
To complete the tasks, work according to the plan given in the left column of the table. In this case, we recommend closing the right column with a sheet of paper. Then you can compare your findings with the solutions shown in the table on the right.


Block 5. Establishing a sequence of actions (UP).
Construction of a segment of a given length.
Option 1. The table contains an entangled algorithm (entangled order of actions) for constructing a segment of a given length (for example, we construct a segment BC \u003d 7 cm). In the left column, an indication of the action in the right column is the result of this action. Rearrange the rows of the table so that the correct algorithm for constructing a segment of a given length is obtained. Record the correct sequence of actions.
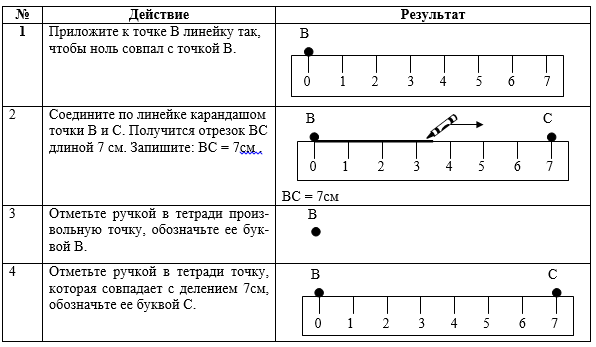
Option 2 The following table shows the algorithm for constructing the segment KM \u003d n cm, where instead of n any number can be substituted. In this embodiment, there is no correspondence between the action and the result. Therefore, it is necessary to establish a sequence of actions, then select a result for each action. Write down the answer in the form: 2a, 1c, 4b, etc.

Option 3 Using the algorithm of option 2, build segments in the notebook with n \u003d 3 cm, n \u003d 10 cm, n \u003d 12 cm.
Block 6. Facet test.
Segment, ray, straight, plane.
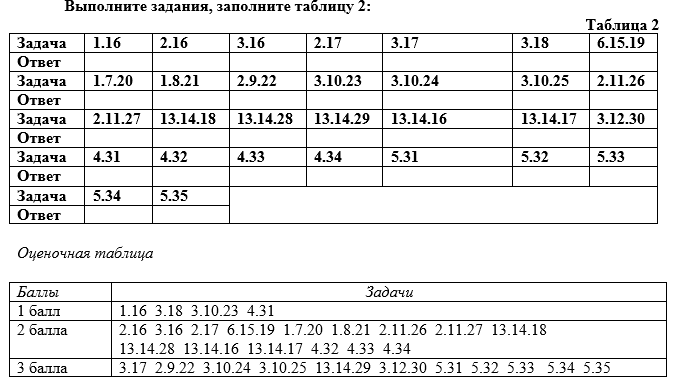
For facet test tasks, drawings and entries numbered 1 to 12 are used, which are shown in Table 1. The task data is generated from them. Then, the requirements of the tasks that are placed in the test after the connective word “TO” are added to them. Answers to the tasks are placed after the word "EQUAL". The set of tasks is shown in Table 2. For example, task 6.15.19 is composed as follows: “IF Figure 6 is used in the task , sthen we add the condition number 15 to it, the task requirement is number 19. ”

13) build four points so that every three of them do not lie on one straight line;
14) draw a line through every two points;
15) mentally extend each of the box surfaces in all directions to infinity;
16) the number of different segments in the figure;
17) the number of different rays in the figure;
18) the number of different lines in the figure;
19) the number of resulting different planes;
20) the length of the AC segment in centimeters;
21) the length of the segment AB in kilometers;
22) the length of the DC segment in meters;
23) the perimeter of the triangle PRQ;
24) the length of the broken QPRMN;
25) quotient of the perimeters of the triangles RMN and PRQ;
26) the length of the segment ED;
27) the length of the segment BE;
28) the number of resulting points of intersection of lines;
29) the number of resulting triangles;
30) the number of parts into which the plane has been divided;
31) the perimeter of the polygon, expressed in meters;
32) the perimeter of the polygon, expressed in decimeters;
33) the perimeter of the polygon, expressed in centimeters;
34) the perimeter of the polygon, expressed in millimeters;
35) the perimeter of the polygon, expressed in kilometers;
EQUAL (equal, has the form):
a) 70; b) 4; c) 217; d) 8; d) 20; e) 10; g) 8 ∙ b; h) 800 ∙ b; i) 8000 ∙ b; j) 80 ∙ b; l) 63000; m) 63; m) 63,000,000; o) 3; o) 6; p) 630,000; c) 6,300,000; t) 7; y) 5; f) 22; x) 28
Block 7. Let's play.
7.1. Mathematical Maze.
The labyrinth consists of ten rooms with three doors each. Each room has one geometric object (it is painted on the wall of the room). Information about this object is in the "guide" through the maze. Reading it, you must go to that room, which is written in the guidebook. Walking through the maze rooms, draw your route. The last two rooms have exits.
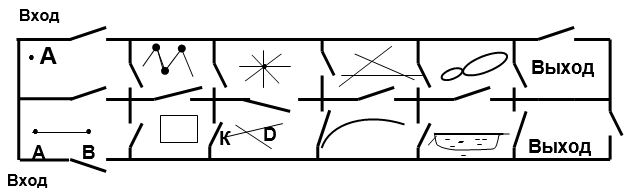
Maze guide
- You must enter the maze through the room, where there is a geometric object that has no beginning, but has two ends.
- The geometric object of this room has no dimensions, it is like a distant star in the night sky.
- The geometric object of this room is composed of four segments having three common points.
- This geometric object consists of four segments with four common points.
- In this room are geometric objects, each of which has a beginning but no end.
- There are two geometric objects that have no beginning or end, but with one common point.
- The idea of \u200b\u200bthis geometric object gives the flight of artillery shells
(trajectory of movement).
- This room has a geometric object with three peaks, but it’s not mountain
- A boomerang flight (hunting) gives an idea of \u200b\u200bthis geometric object.
weapons of indigenous people of Australia). In physics, this line is called the trajectory.
body movements.
- The idea of \u200b\u200bthis geometric object is given by the surface of the lake in
calm weather.
Now you can exit the maze.
In the maze there are geometric objects: plane, open line, straight line, triangle, point, closed line, broken line, line segment, ray, quadrangle.
7.2. Perimeter of geometric shapes.
In the figures, highlight the geometric shapes: triangles, quadrangles, five - and hexagons. Use the ruler (in millimeters) to determine the perimeters of some of them.

7.3. Relay race of geometric objects.
Relay tasks have empty frames. Write a missing word in them. Then drag this word into another frame, where the arrow shows. In this case, you can change the case of this word. Passing through the relay stages, complete the required constructions. If you pass the baton correctly, then in the end you will receive the word: perimeter.

7.4. The fortress of geometric objects.
Read § 2, write out the names of geometric objects from his text. Then write these words in the empty cells of the "fortress."
 Subject: Ray. Comparison of a beam with a segment, with a straight line. Beam building.
Subject: Ray. Comparison of a beam with a segment, with a straight line. Beam building.
Goal. To acquaint with a geometric figure - a ray.Tasks. Educational: - form an idea of \u200b\u200bthe concept of the beam;
Repeat the composition of the number 9;
Improve oral counting skills;
To consolidate knowledge of education, naming, writing and comparing the numbers of the second ten.
Developing :
To develop the ability to distinguish between a line and a ray, to compare a line and a ray, a segment and a ray, a point and a ray; - develop practical skills in beam construction, develop spatial representations; - develop visual memory and attention, auditory perception through auditory instruction.
Educational: - bring up disciplinary skills, accuracy, independence, interest in learning, subject. Corrective: - to correct certain aspects of mental activity: analysis and synthesis operations, identifying the main thing, establishing logical and cause-effect relationships, the culture of mathematical speech; - improve movement and sensorimotor development:fine motor skills of the hands (to form manual skill, to develop rhythm, smoothness and proportionality of movements); - adjust and develop tactile perception, memory.
Equipment : computer, projector, presentation for the lesson, threads, rulers, pencils, abacus, counting material.
During the classes
1.Org - moment
2.Top post
Today we will make an exciting journey to the country of Geometry. We learn about another geometric figure. And throughout the lesson, the warm sun will shine on us. And it has prepared you wishes:
“Be brave, kind, active. Good luck to you! ”
3.Oral account
What is the number: 15, 19, 10, 14, 11, 20, 18 (3slide)
What are the neighbors (4slide)
Compare numbers (5slide)
(5slide) By what signs can these figures be separated?
1) In shape(write down the corresponding expression on the board) 4 + 5 \u003d 9 2) By color 3 + 6 \u003d 9 3) By size 2 + 7 \u003d 9 4) By mood 8 + 1 \u003d 9 - Look at the expressions. Composition, how many remembered? (9) - Today, a minute of calligraphy will be devoted to the number 9. (6 slide) - Well done! They managed the verbal account. The sun shines for us even brighter and warmer.
4.New material (7slide) Work with handouts. - Read what words you got? (line, line, point, ray) - What are the lines in the picture. How many straight lines? How many curves? How many segments? Which line is left?(find it difficult to answer) -This line is called a ray. - draw a line(in a notebook and on a blackboard) - What is a straight line? What property of the line do you know about?(she is endless) - To one side I take and attach a yellow circle. Can this line now be supplemented in both directions? (no) What does it look like?(on a sunbeam) This figure is called a ray. How many points on the ray?(one) A point is the beginning of a ray. Does the ray have an end? - Remember, the ray has a beginning and no end.(8-10 slide) Is it possible to measure the length of the beam? Why? - Compare the line and the beam. - Then I attach a circle on the other side. Now you can continue straight in both directions? What kind of figure did you get? - Compare the beam and the segment.(11slide) - What is the direct number? Section? Ray? (answers are commented).(12slide)
Physminute
(13slide) What is it? () We each have a name, let's call point A.
How many lines passes through point A? (3) And how much more can be spent?(a bunch of) Put a point in the notebook, name it O and draw a few straight lines(checking)
5. Work with the textbook p. 80 No. 7, No. 8
6. Independent work
I give everyone a test:
Circle the intersecting rays in red, the blue disjoint. How many rays? (4)
(14slide) Solve the short record problem.
M. - 6 rays
FROM. - ? 2 more than M.(1 student decides at the blackboard)
6.Total - What new geometric figure did we meet? What mood did you come to the end of the lesson?(The sun gives prizes to active children )


