This is a closed flat line, every point of which is equidistant from the same point ( O) called the center.

Direct ( Oa, OB, OS .  .) connecting the center with the points of the circle is   radii.

From this we get:

1. All radii of one circlesare equal.

2. Two circles with the same radii will be equal.

3. Diameterequal to two radii.

4. Pointlying inside the circle, closer to the center, and a point lying outside the circle, further from the center than the points of the circle.

5. Diameter, perpendicular to the chord, divides this chord and both arcs pulled by it in half.

6. Arcsconcluded between parallel chordsare equal.

When working with circles, the following theorems apply:

1. Theorem . A straight line and a circle cannot have more than two common points.

From this theorem we obtain two logical consequences consequences:

No part circlescannot be compatible with the line, because otherwise the circle with the line would have more than two points in common.

A line, no part of which can be combined with a line, is called crooked.

From the previous it follows that the circle is curve line.

2. Theorem . Through any three points that do not lie on one straight line, you can draw a circle and only one.

how consequenceof this theorem we get:

Three perpendicularto the sides the triangle  inscribed in a circle drawn through their midpoints intersect at one point, which is the center of the circle.

Let's solve the problem. It is required to find the center proposed circles.

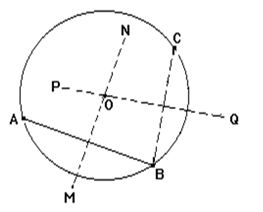
We mark on the proposed three any points A, B, and C, draw two through them chords, for example, AB and CB, and from the middle of these chords we indicate perpendicularsMN and PQ. The desired center, being equally distant from A, B, and C, must lie on MN and PQ, therefore, it is located at the intersection of these perpendiculars, i.e. at point O.

In this lesson, we will introduce you to the concepts of circle and circle. Learn to draw a circle and circle.

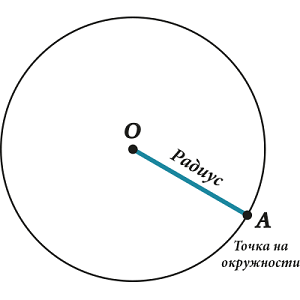
You learned to draw circles in the lower grades. Let's remember how this process happens. In order to draw a circle, we must set the point of the compass at some point O. Next, we will rotate the leg with a pencil.

Definition

A pencil will draw a line on the sheet plane, which is called circumference . The point at which the point of the compass was set, or the point O, is called circle center .

Let's connect the center of the circle, i.e. point Oh, with any point on the circle you like. We denote this point, for example, by the letter A. We see that we have obtained the segment OA.

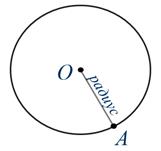
Definition

The line connecting the center of the circle to any point on the circle is called radius . Radius is denoted by a small Latin letter r.

Let's mark some more points on this circle, for example, B, C and D. And we will connect them with the center of the circle. These segments of OB, OS and OD are also called radii .

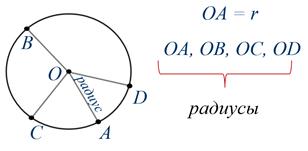
All points of the circle are equidistant from its center, i.e. removed from the center at a distance equal to the length of the radius.

Often the word " length"Do not pronounce, but instead of" radius length"They say just" radius". For example, they say: " A circle with a radius of 3 cm is shown. "

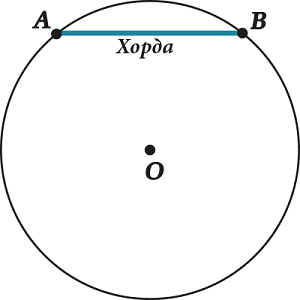
Now let's connect any 2 points on the circle that do not pass through the center of the circle, for example, E and F. We have obtained the segment EF.

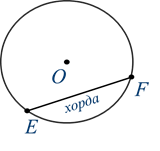
Definition

A segment whose ends lie on a circle is called chord .

A chord passing through the center of a circle is called it diameter .

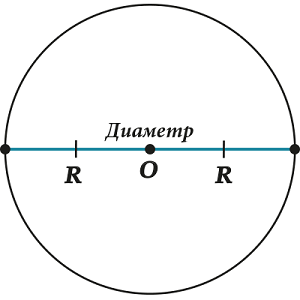
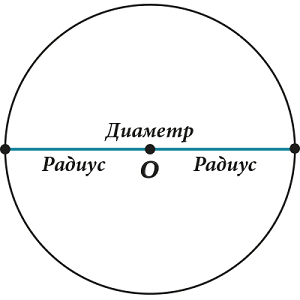
Look carefully at the screen. The figure shows the segment AB, it is diameter   circles. According to the figure, it is easy to see that the diameter of the circle is equal to its two radii, i.e.

Diameter is indicated by a small Latin letter dthen d = 2 r.

Remember the diameter of the circle is two times longer than the radius.

All circle diameters are equal to each other.

Mark 2 points on the circle, for example, M and N.

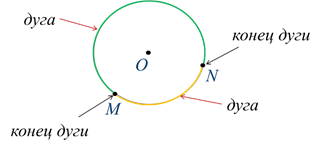
Definition

These 2 points divided the circle into 2 parts, each of which is called an arc .

In our figure, they are depicted with lines of different colors.

Points M and N are called ends of arcs.

Circle is closed line.  She breaks the plane into two parts - internal and external.

The part of the plane inside the circle, together with this circle, is called the circle.

Circle   - this is border  circle. Center   the circle is called center of this circle. Radius   the circle is called radius of this circle. Diameter   the circle is called diameter of this circle. Chord   the circle is called chord of this circle.

A circle consists of points remote from a given point (its center) by a distance less than or equal to its radius.

Definition

If two radii of the circle are drawn in the circle, for example, OA and OV, they will separate from the circle its part, which sector.

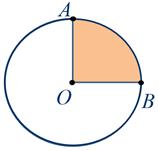
In our case, the AOB sector has turned out. The rest of the circle is also a sector.

Now let's figure out the location of the points, circle and circle. Look carefully at the screen.

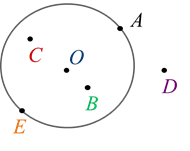
It depicts a circle centered at point O and points A, B, C, D and E.

Points A and E lie on a circle  or you can still say belong to  her.

Points B, C, D, O don't belong  this circle.

Points A, B, C, E and O belong to the circle.

Point D is out of a circle  or out of circle.

Summary

So, today in the lesson we got acquainted with the concepts of circle, circle and their elements. And also learned to draw them.

Key terms.

Do you remember all the names associated with the circle well? Just in case, recall - look at the pictures - refresh your knowledge.

Firstly - the center of the circle is such a point, the distances from which to all points of the circle are the same.

Secondly -   radius - the line connecting the center and the point on the circle.

There are a lot of radii (as many as points on the circle), but   all radii have the same length.

Sometimes for brevity radius  called exactly cut length  “The center is a point on the circle”, and not the segment itself.

But what happens if you connect two points on a circle? Same segment?

So, this segment is called "chord".

There is another accepted expression: "a chord pulls together an arc." Here, in the figure, for example, a chord pulls together an arc. And if the chord suddenly passes through the center, then it has a special name: "diameter".

As in the case of the radius, the diameter is often called the length of the segment connecting two points on the circle and passing through the center. By the way, how are the diameter and radius related? Look carefully. Of course, the radius is half the diameter.

In addition to chords, there are also secant.

Remember the simplest?

And now - the names for the corners.

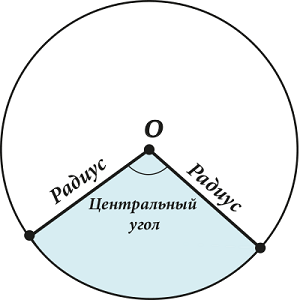
Central angle - the angle between two radii.

Naturally, isn't it? The sides of the corner extend from the center - which means that the angle is central.

And now - the inscribed angle

Inscribed angle - the angle between two chords that intersect at a point on a circle.

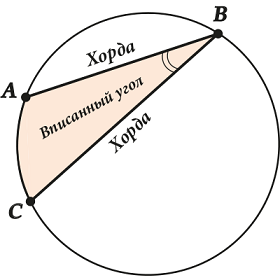
At the same time, they say that the inscribed angle is based on an arc (or a chord).

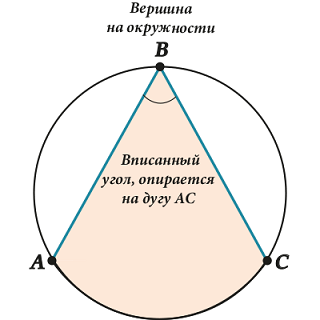
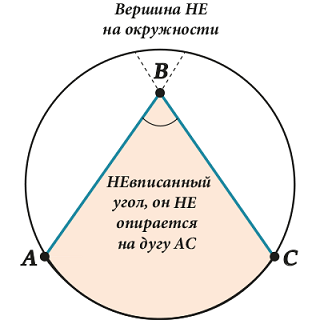
Here sometimes difficulties arise. Pay attention - NOT ANY angle inside the circle - inscribed,  but only one with the top “sitting” on the circumference itself.

Look at the picture:

Measurement of arcs and angles.

Circumference. Arcs and angles are measured in degrees and radians. First about the degrees. There are no problems for angles - you need to learn how to measure an arc in degrees.

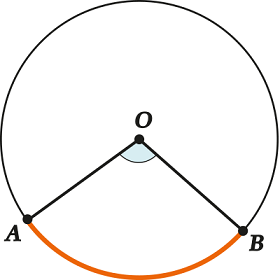
Degree measure (arc value) is the value (in degrees) of the corresponding central angle

What does the word “corresponding” mean here? We look carefully:

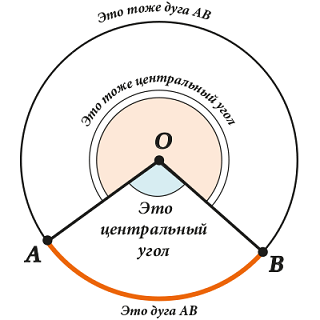
Do you see two arcs and two central corners? Well, a larger angle corresponds to a larger arc (and it’s okay that it is larger), and a smaller angle corresponds to a smaller arc.

So, we agreed: the arc contains as many degrees as in the corresponding central angle.

And now about the terrible - about radians!

What kind of beast is this “radian”?

Imagine this: radians are a way to measure the angle ... in radii!

An angle of radian is such a central angle whose arc length is equal to the radius of the circle.

Then the question arises - how many radians are in the deployed angle?

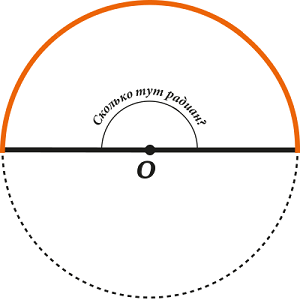
In other words: how many radii "fit" in half a circle? Or another way: how many times is the length of half the circumference greater than the radius?

This question was asked by scientists in ancient Greece.

And so, after a long search, they found that the ratio of the circumference to the radius does not want to be expressed by “human” numbers like, etc.

And you can’t even express this attitude through the roots. That is, it turns out that it cannot be said that half the circumference is times or times the radius! Can you imagine how amazing it was to discover people for the first time ?! For the ratio of half circle length to radius, “normal” numbers were enough. I had to enter a letter.

So, this is a number expressing the ratio of the length of the semicircle to the radius.

Now we can answer the question: how many radians are in the deployed angle? There is a radian in it. It is because half the circumference is times the radius.

Ancient (and not so) people for centuries (!)   they tried to more accurately calculate this mysterious number, it is better to express it (at least approximately) through "ordinary" numbers. And now we are lazy to the impossibility - two signs after the busy one are enough for us, we are used to

Think about it, this means, for example, that y of a circle with a radius of one is approximately equal in length, and it’s just impossible to write down this length with a “human” number - you need a letter. And then this circumference will be equal. And of course, the circumference of the radius is equal.

Back to the radians.

We have already found out that there is a radian in the expanded angle.

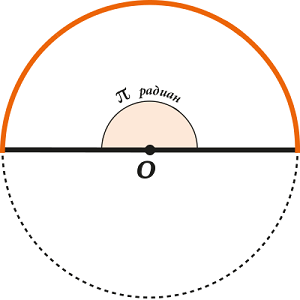
What do we have:

So glad., That is, glad. In the same way, a plate with the most popular corners is obtained.

The ratio between the inscribed and central angles.

There is an amazing fact:

The value of the inscribed angle is half that of the corresponding central angle.

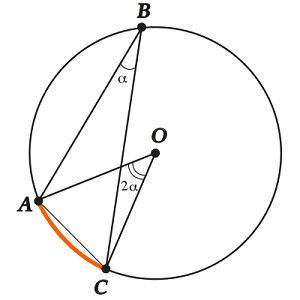
See how this statement looks in the picture. A “corresponding” central angle is one where the ends coincide with the ends of the inscribed angle and the vertex is in the center. And at the same time, the “corresponding” central angle should “look” at the same chord () as the inscribed angle.

Why so? Let's look at a simple case first. Let one of the chords go through the center. It happens sometimes, right?

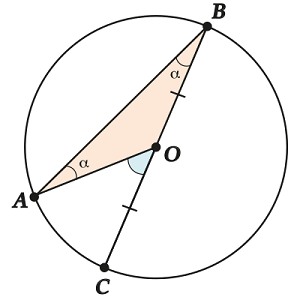
What is going on here? Consider. It is isosceles - after all - and radii. Hence, (designated them).

Now let's look at. This is the outside corner for! Recall that the outer corner equal to the amounts  two internal, not adjacent to it, and write:

I.e! Unexpected effect. But there is a central angle for the inscribed.

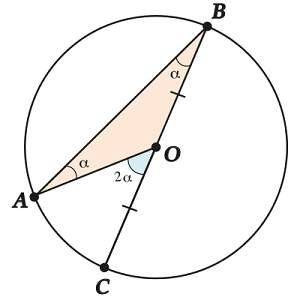
So, for this case, they proved that the central angle is twice as large as the inscribed one. But it is a painful special case: the truth is, far from always the chord passes straight through the center? But nothing, now this particular case will help us a lot. Look: the second case: let the center lie inside.

Let's do this: draw a diameter. And then ... we see two pictures that were already taken apart in the first case. Therefore, we already have that

Hence (in the drawing, a)

Well, the last case remained: the center is out of the corner.

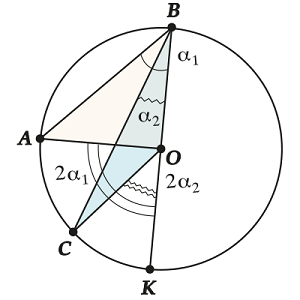
We do the same: draw a diameter through a point. All the same, but instead of the sum - the difference.

That's all!

Let's now form two main and very important consequences from the statement that the inscribed angle is half the central angle.

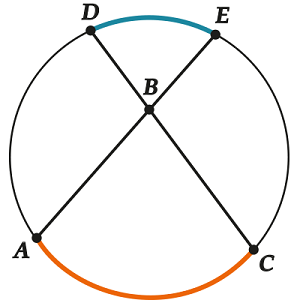
Corollary 1

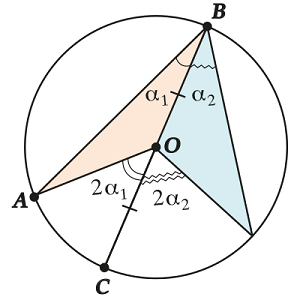
All inscribed angles, based on one arc, are equal to each other.

We illustrate:

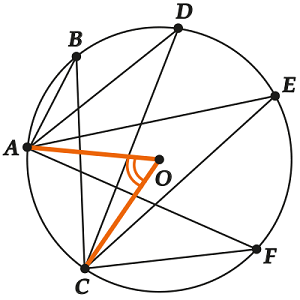
The inscribed angles based on the same arc (we have this arc) are countless, they can look very different, but they all have the same central angle (), which means that all these inscribed angles are equal between themselves.

Corollary 2

The angle based on the diameter is straight.

See: which corner is central to?

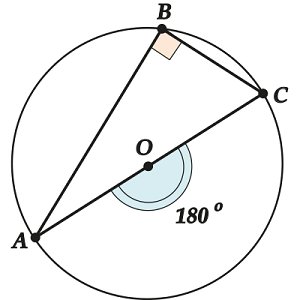
Of course, . But he is equal! Well, that's why (and also a lot of inscribed angles based on) it is equal.

The angle between two chords and secants

But what if the angle of interest to us is NOT inscribed and NOT central, but, for example, this:

or such?

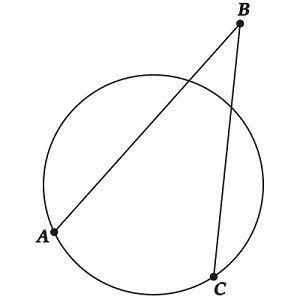
Is it possible to somehow express it all the same through some central corners? It turns out you can. Look: we are interested.

a) (as the external angle for). But - inscribed, relies on an arc -. - inscribed, relies on an arc.

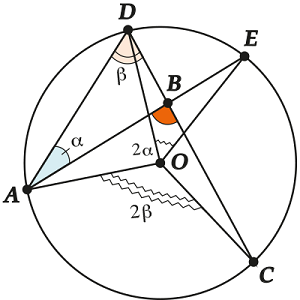
For beauty they say:

The angle between the chords is equal to half the sum of the angular values \u200b\u200bof the arcs enclosed in this angle.

This is written for brevity, but of course, when using this formula, you need to keep in mind the central angles

b) And now - “outside”! How to be? Yes, almost the same! Only now (again apply the outer corner property for). That is now.

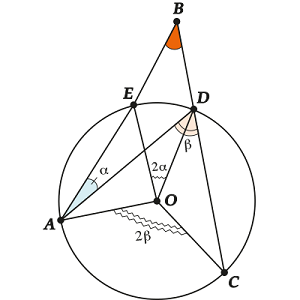
And that means. Let's bring beauty and brevity to the notes and formulations:

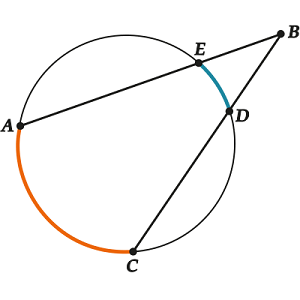
The angle between the secants is equal to the half-difference of the angular values \u200b\u200bof the arcs enclosed in this angle.

Well, now you are armed with all the basic knowledge about the corners associated with a circle. Go ahead to storm the challenges!