Mathematical expressions (formulas) abbreviated multiplication (the square of the sum and difference, the cube of the sum and difference, the difference of squares, the sum and difference of the cubes) are extremely non-replaceable in many areas of the exact sciences. These 7 character entries are not interchangeable when simplifying expressions, solving equations, multiplying polynomials, reducing fractions, solving integrals, and much more. So it will be very useful to understand how they are obtained, why they are needed, and most importantly, how to remember them and then apply them. Then applying abbreviation formulas in practice, the hardest thing to see is xand what u have. Obviously, there are no restrictions for a and bno, which means it can be any number or letter expression.
And so they are:
First x 2 - at 2 \u003d (x - y) (x + y) .To calculate square difference of two expressions it is necessary to multiply the differences of these expressions by their sums.
Second (x + y) 2 \u003d x 2 + 2hu + y 2 . To find squared amount of two expressions, you need to add the double product of the first expression to the second plus the square of the second expression to the square of the first expression.
Third (x - y) 2 \u003d x 2 - 2hu + y 2. To calculate difference squareof two expressions it is necessary to subtract the double product of the first expression by the second plus the square of the second expression from the square of the first expression.
Fourth (x + y) 3 \u003d x 3 + 3x 2 y + 3hu 2 + at 3. To calculate cube amountof two expressions, add the triple product of the square of the first expression to the second plus the triple product of the first expression and the square of the second plus the cube of the second expression to the cube of the first expression.
Fifth (x - y) 3 \u003d x 3 - 3x 2 y + 3hu 2 - at 3. To calculate difference cubeof two expressions it is necessary to subtract from the cube of the first expression the triple product of the square of the first expression by the second plus the triple product of the first expression by the square of the second minus the cube of the second expression.
Sixth x 3 + at 3 \u003d (x + y) (x 2 - xy + y 2) To calculate amount of cubestwo expressions you need to multiply the sum of the first and second expression by the incomplete square of the difference of these expressions.
Seventh x 3 - at 3 \u003d (x - y) (x 2 + xy + y 2) To make a calculation difference cubesof two expressions, multiply the difference between the first and second expressions by the incomplete square of the sum of these expressions.
It is not difficult to remember that all formulas are used to perform calculations in the opposite direction (from right to left).
The existence of these laws was discovered about 4 thousand years ago. They were widely used by the inhabitants of ancient Babylon and Egypt. But in those eras, they were expressed verbally or geometrically and did not use letters in the calculations.
We will analyze squared proof(a + b) 2 \u003d a 2 + 2ab + b 2.
First this mathematical pattern proved the ancient Greek scientist Euclid, who worked in Alexandria in the III century BC, he used the geometric way of proving the formula for this, since the scientists of ancient Hellas did not use letters to indicate numbers. They used everywhere not “a 2”, but “a square on segment a”, not “ab”, but “a rectangle enclosed between segments a and b”.
And so Euclid took a square with a side (a + b):
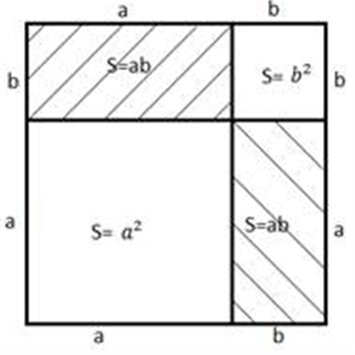
On the other hand, he will present the same square differently, dividing the side into but and b:
Then the square area can be represented as the sum of the areas:
And since the squares were the same, their areas are equal, and this means:
Thus, it was proved geometrically sum squared formula.
When calculating algebraic polynomials to simplify the calculations used abbreviation formulas . There are seven such formulas. They all need to know by heart.
It should also be remembered that instead of a and b in the formulas there can be both numbers and any other algebraic polynomials.
Square difference
The difference of the squares of two numbers is equal to the product of the difference of these numbers and their sum.
a 2 - b 2 \u003d (a - b) (a + b)
Amount squared
The square of the sum of two numbers equals square the first number plus the double product of the first number and the second plus the square of the second number.
(a + b) 2 \u003d a 2 + 2ab + b 2
Note that using this abbreviation formula is easy find squares of large numberswithout using a calculator or column multiplication. Let us illustrate with an example:
Find 112 2.
Let us decompose 112 into the sum of numbers whose squares we remember well.
112 = 100 + 1
Write the sum of the numbers in brackets and put a square over the brackets.
112 2 = (100 + 12) 2
We use the formula of the square of the sum:
112 2 \u003d (100 + 12) 2 \u003d 100 2 + 2 x 100 x 12 + 12 2 \u003d 10 000 + 2 400 + 144 \u003d 12 544
Remember that the square sum formula is also valid for any algebraic polynomials.
(8a + s) 2 \u003d 64a 2 + 16ac + c 2
Warning!!!
(a + b) 2 not equal to a 2 + b 2
Difference square
The square of the difference of two numbers is equal to the square of the first number minus the double product of the first and second plus the square of the second number.
(a - b) 2 \u003d a 2 - 2ab + b 2
It is also worth remembering a very useful transformation:
(a - b) 2 \u003d (b - a) 2
The formula above is proved by simply opening the brackets:
(a - b) 2 \u003d a 2 - 2ab + b 2 \u003d b 2 - 2ab + a 2 \u003d (b - a) 2
Cube Amount
The cube of the sum of two numbers is equal to the cube of the first number plus three times the product of the square of the first number and the second plus three times the product of the first and the square of the second plus the cube of the second.
(a + b) 3 \u003d a 3 + 3a 2 b + 3ab 2 + b 3
Remembering this страш scary ’-looking formula is pretty simple.
Learn that a 3 goes at the beginning.
The two polynomials in the middle have coefficients of 3.
INrecall that any number to the zero degree is 1. (a 0 \u003d 1, b 0 \u003d 1). It is easy to see that in the formula there is a decrease in degree a and an increase in degree b. You can verify this:
(a + b) 3 \u003d a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 \u003d a 3 + 3a 2 b + 3ab 2 + b 3
Warning!!!
(a + b) 3 not equal to a 3 + b 3
Cube of difference
The cube of the difference of two numbers is equal to the cube of the first number minus three times the product of the square of the first number and the second plus three times the product of the first number and the square of the second minus the second cube.
(a - b) 3 \u003d a 3 - 3a 2 b + 3ab 2 - b 3
This formula is remembered as the previous one, but only taking into account the alternation of the signs "+" and "-". The first member of a 3 is preceded by a “+” (according to the rules of mathematics, we do not write it). So, the next member will be “-”, then again “+”, etc.
(a - b) 3 \u003d + a 3 - 3a 2 b + 3ab 2 - b 3 \u003d a 3 - 3a 2 b + 3ab 2 - b 3
Sum of cubes ( Not to be confused with the cube of the amount!)
The sum of the cubes is the product of the sum of two numbers by the incomplete square of the difference.
a 3 + b 3 \u003d (a + b) (a 2 - ab + b 2)
The sum of the cubes is the product of two brackets.
The first bracket is the sum of two numbers.
The second bracket is the incomplete square of the difference of numbers. An incomplete squared difference is the expression:
A 2 - ab + b 2
This square is incomplete, since in the middle, instead of the doubled product, is the usual product of numbers.
Difference of cubes (Not to be confused with a difference cube !!!)
The difference of the cubes is the product of the difference of two numbers by the incomplete square of the sum.
a 3 - b 3 \u003d (a - b) (a 2 + ab + b 2)
Be careful when writing characters.It should be remembered that all the formulas above are also used from right to left.
An easy way to remember the formulas of abbreviated multiplication, or ... Pascal's triangle.
Are abbreviation formulas difficult to remember? The case is easy to help. You just need to remember how such a simple thing as the Pascal triangle is depicted. Then you will remember these formulas always and everywhere, or rather, do not remember, but restore.
What is the Pascal Triangle? This triangle consists of coefficients that go into the decomposition of any degree of a binomial of the form into a polynomial.
We decompose, for example,:
In this record it is easy to remember that at first there is a cube of the first, and at the end - a cube of the second number. But what’s in the middle is difficult to remember. And even the fact that in each next term the degree of one factor decreases all the time, and the second one increases, it is easy to notice and remember, it is more difficult to remember coefficients and signs (plus or minus?).
So first, the odds. No need to remember them! In the fields of the notebook, we quickly draw a Pascal triangle, and here they are - the coefficients are already in front of us. We start drawing with three ones, one on top, two below, to the right and left - yeah, already a triangle turns out:

The first line, with one unit, is zero. Then comes the first, second, third and so on. To get the second line, you need to assign the units again at the edges, and in the center write the number obtained by adding the two numbers above it:
As you may have guessed, we get in each line the coefficients from the decomposition of the binomial into the polynomial:
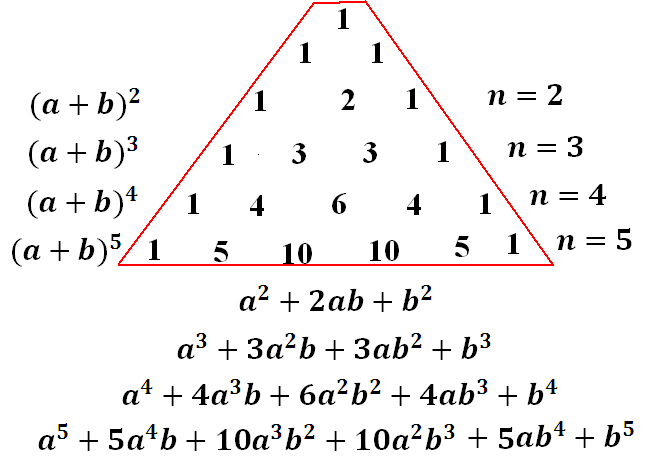
Well, the signs are even easier to remember: the first is the same as in the expandable binomial (expanding the sum means plus, the difference means minus), and then the signs alternate!
This is such a useful thing - Pascal's triangle. Use it!
At the origins of this project is a small formula that I noticed this year. More specifically, this is a pattern between numbers. I have long been interested in what this formula is, but different people assumed completely different options. Since, of course, this formula is connected with squares of numbers, and I don’t know if anyone came up with it before me, I decided to make a presentation in which, besides this regularity, I talked about some interesting topic. So I decided to create this research project.
Amount squared
Let's start with the basics. Surely, every seventh grader (not to mention older students) knows this formula. But still, to consolidate the material, it is worth checking this knowledge.
(x + y) ² \u003d x² + 2xy + y²
What reads like\u003e.
Difference square
But on this topic, difficulties are already beginning to occur. Unfortunately, not all students remember this formula, some are confused, but I hope that none of our class will be mistaken either in the record or in the wording.
(x-y) ² \u003d x²-2xy + y²
And this formula is read:\u003e.
A bit of history. So we remembered the first two formulas of abbreviated multiplication. As it turned out, there is nothing wrong with that!
Have you ever wondered who did come up with these two formulas: the square of the sum and the square of the difference? Some sources say that it was the ancient Greek mathematician Euclid. It was a truly unique discovery, since we know that he lived back in the 3rd century BC.
Square difference
So we got to the last formula related to the squares of numbers. In the next slide, I will prove why she is the last. In the meantime, let's try to recall the difference of the squares.
x²-y² \u003d (x + y) (x-y)
It should be remembered that the factors can be reversed.
The difference of the squares of two numbers is equal to the product of the sum and the difference of these numbers.
Sum of squares
But the concept of this formula of abbreviated multiplication is not given in the school course, because it simply does not exist. And now we will consider why.
- The square of the sum and the square of the difference can be expanded not only by the formula given earlier. They can be represented as follows: (x + y) ² \u003d (x + y) (x + y) and (x-y) ² \u003d (x-y) (x-y).
- Based on the fact that the first three formulas of abbreviated multiplication can be represented as a product of two polynomials, it can be argued that the sum of squares can be represented as a product of two polynomials.
- But all possible combinations have already been used. The squared sum is the product of the sums of these numbers, the squared difference is the product of the differences of these numbers, and the difference of the squares is the product of the sum and the difference. Therefore, the sum of squares cannot be represented in the form of a formula of abbreviated multiplication.
Incomplete square
For further repetition of the abbreviated multiplication formulas, we must also recall another term. We examined the concepts of squared sum and squared difference ((x + y) ² \u003d x² + 2xy + y² and (x-y) ² \u003d x²-2xy + y²). So then what is an incomplete square? We need an incomplete square of the sum and an incomplete square of the difference. The partial square of the sum is x² + xy + y² (the sum of the square of the first number, the product of the first number on the second and second numbers), and the partial square of the difference is x²-xy + y² (the square of the first number minus the product of the first number on the second plus the square of the second numbers). As we see, in both cases, instead of doubling the product of the first number to the second, the product of the first number and the second appears.
Sum of cubes
So we started the moment, which, I suspect, few people remember. Time to test knowledge.
x³ + y³ \u003d (x + y) (x²-xy + y²)
The sum of the cubes of two numbers is equal to the product of these numbers and the incomplete square of their sum.
Cubes difference
And now we recall another formula, very similar to the previous one.
x³-y³ \u003d (x-y) (x² + xy + y²)
Reads:\u003e.
Cube Amount
This formula and the one following it is a little difficult to remember, but I still hope that there are students in our class with a good memory, which we will check now.
(x + y) ³ \u003d x³ + 3x²y + 3xy² + y³
The cube of the sum of two numbers is equal to the sum of the square of the first number, the triple product of the square of the first number and the second, the triple product of the first number and the square of the second and the cube of the second number.
Cube of difference
And finally, we got to the last formula studied in the seventh grade.
(x-y) ³ \u003d x³-3x²y + 3xy²-y³
The cube of the difference of two numbers is equal to the cube of the first number minus three times the product of the square of the first number and the second plus three times the product of the first number and the square of the second minus the cube of the second number.
In the previous lesson, we figured out the factorization. Learned two ways: making common factor for brackets and grouping. In this tutorial is the following powerful way: abbreviated multiplication formulas. In a brief record - FSU.
The formulas of abbreviated multiplication (the square of the sum and difference, the cube of the sum and difference, the difference of squares, the sum and difference of cubes) are extremely necessary in all sections of mathematics. They are used in simplifying expressions, solving equations, multiplying polynomials, reducing fractions, solving integrals, etc. etc. In short, there is every reason to deal with them. Understand where they come from, why they are needed, how to remember them and how to apply them.
Understand?)
Where do shorthand multiplication formulas come from?
Equalities 6 and 7 are not very familiar. It’s the other way around. This is special.) Any equality works both from left to right, and from right to left. In such a record, it is clearer where the FSU comes from.
They are taken from multiplication.) For example:
(a + b) 2 \u003d (a + b) (a + b) \u003d a 2 + ab + ba + b 2 \u003d a 2 + 2ab + b 2
That's all, no scientific tricks. Just multiply the brackets and give similar ones. So it turns out all formulas of abbreviated multiplication. Abbreviated multiplication - this is because in the formulas themselves there is no multiplication of brackets and reduction of similar ones. Reduced.) Immediately given the result.
FSU need to know by heart. Without the first three, you can not dream of a trio, without the rest - of a four and a five.)
Why do you need abbreviation formulas?
There are two reasons to learn, even memorize, these formulas. The first - a ready-made answer on the machine dramatically reduces the number of errors. But this is not the main reason. But the second ...
If you like this site ...
By the way, I have a couple more interesting sites for you.)
You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)
You can get acquainted with functions and derivatives.
So ... We all heard about them and saw these formulas:
But, as a rule, few people understand why to remember these formulas? How can they be useful in the calculations? And one more important question HOW can they BE REMEMBERED AT ALL ?! Let’s talk about everything in order, but first we’ll touch on the issue of putting them into practice.
The name "" is not at all accidental.
Take the simplest first formula squared amount - and try to consistently square the amount in brackets, that is, multiply by itself:
Look, what else can be done with the expression that we have got? Correctly, cite the following terms:
Thus output all abbreviation formulas. You can output them each time yourself, but you can save time and quickly calculate the necessary example, knowing the final value of the formulas.
And we painted the multiplication of only the first bracket, and the same thing needs to be done with the second and the third ... Agree, getting confused is very easy, and, as a rule, the answer of the whole example depends on how you find this simple action.
Thus, abbreviation formulas allow you to reduce the laborious multiplication of members on each other and get a quick result.
As the formula for the squared sum is derived, we described earlier. Let's try to perform similar actions with the square of the difference.
The square of the difference means to multiply by itself. Try to derive the formula for this expression yourself, by analogy with the square of the sum.
Did you do it? Let's see how you opened the brackets:
You probably already noticed a certain pattern? Take a close look at the formulas. What is their difference?
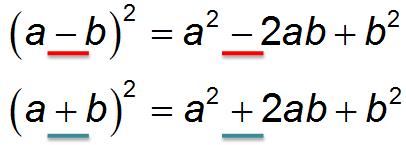
Of course, you saw that if we square the difference between and, then we subtract their double product, and if we square the amount, then we add. When squaring the difference and amount, do not forget about the double product of numbers and! This is the grossest and most common mistake!
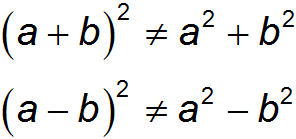
Abbreviated Multiplication Formulas. Examples.
Now you will say: “It is clear that with the help of formulas I can quickly convert examples and most likely I will come to the correct answer in them, but how can they come in handy for me just like that? In life?"
It is very easy! How much will? No need to rush to multiply by in a column, and even more so it is not worth typing numbers on a calculator. Just imagine how the sum and squared it. Happened? Compare your thoughts:
Using formulas squared sum and squared difference we can easily find the squares of large numbers without using a calculator and not counting in a column. You just need to present the number as the sum (or difference) of the numbers whose square we know well.
Abbreviated Multiplication Formulas. Training.
Try to calculate the following expressions in this way:
Answers:
Or, if you know the squares of the basic two-digit numbers, remember how much will be? Remembered? . Fine! Since we are squaring, we must multiply by. It turns out that.
Remember that the squared sum and squared difference formulas are valid not only for numerical expressions:
Count the following expressions yourself:
Did you get the following?
Abbreviated Multiplication Formulas. Total.
To summarize and write down the formulas of the square of the sum and the difference in one line:
Now let's practice “collecting” the formula from the decomposed view to the view. We will need this skill in the future when converting large expressions.
Let's say we have the following expression:
We know that the square of the sum (or difference) is square of one number squared another number and double product of these numbers.
In this problem, it is easy to see the square of one number - this. Accordingly, one of the numbers in the bracket is the square root of, that is:
Since the second term is, then this is the double product of one and the other number, respectively:
Where is the second number in our bracket.
The second number in the bracket is equal.
Check it out. should be equal. Indeed it is, that means we found both numbers in brackets: and. It remains to determine the sign that stands between them. What do you think the sign will be there?
Correctly! So how are we add doubled product, then between the numbers there will be a sign of addition. Now write the converted expression. Did you do it? You should have the following:
Note: changing the positions of the terms does not affect the result (it does not matter, addition or subtraction is between and).
It is not necessary that the numbers in the converted expression stand as written in the formula. Look at this expression:. Try to convert it yourself. Happened?
Well done! Practice - Convert the following expressions:
Answers:
- - prove that it is equivalent.
Did you do it? Fix the topic. Choose from the expressions below those that can be represented as a squared sum or difference.
- - can not be imagined as a square; one would imagine if, instead, it was.
Square difference
Another formula for abbreviated multiplication is the square difference.
The difference of the squares is not the square of the difference!
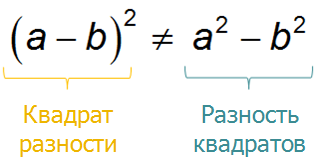
The difference of the squares of two numbers is equal to the product of the sum of these numbers by their difference:
Check if this formula is correct. To do this, we multiply, as was done when deriving the squared formulas of the sum and difference:
So we just made sure that the formula is really correct. This formula also simplifies complex computational operations. Here is an example:
It is necessary to calculate:. Of course, we can square, then square and subtract one from the other, but the formula simplifies our task:
Happened? Check the results:
As well as the square of the sum (difference), the formula of the difference of squares can be applied not only with numbers:
The ability to decompose the difference of the squares will help us transform complex mathematical expressions.
Please note that:
When expanding the square of the difference of the right expression, we get:
Be careful and see what specific term is squared! To fix the topic, transform the following expressions:
Wrote down? Compare the resulting expressions:
Now that you have learned the square of the sum and the square of the difference, as well as the difference of the squares, let’s try to solve the examples by combining these three formulas.
Conversion of elementary expressions (square of the sum, square of the difference, difference of squares)
Suppose we are given an example:
This expression needs to be simplified. Look carefully, what do you see in the numerator? That's right, the numerator is a full square:
To simplify the expression, remember that the hint in which direction to move in simplification is in the denominator (or in the numerator). In our case, when the denominator is expanded, and nothing else can be done, we can understand that the numerator will be either the square of the sum or the square of the difference. As we add, it becomes clear that the numerator is the square of the sum.
Try transforming the following expressions yourself:
Happened? Compare the answers and move on!
Sum cube and difference cube
The formulas cube sum and cube difference are displayed in the same way as squared amount and difference square: disclosure of brackets when multiplying members by each other.
If the square of the sum and the square of the difference are very easy to remember, then the question arises: “how to remember cubes?”
Look carefully at the two formulas described in comparison with squaring similar terms:
What pattern do you see?
1. When erected in square we have square first day and square second; when erected into a cube - there is cube one number and cube another number.
2. When erected in square, we have doubled the product of numbers (numbers in 1 degree, which is one degree less than the one into which we raise the expression); at construction in cube – tripled the product in which one of the numbers is squared (which is also 1 degree less than the degree to which the expression is raised).
3. When squaring the sign in brackets in the open expression is reflected when adding (or subtracting) the doubled product - if the addition is in brackets, then we add, if subtraction is subtracted; when building a cube, the rule is this: if we have a sum cube, then all the signs are “+”, and if there is a difference cube, then the signs alternate: “” - “” - “” - “”.
All of the above except the dependence of the degrees when multiplying members is shown in the figure.
Practice it? Open the brackets in the following expressions:
Compare the resulting expressions:
Difference and Sum of Cubes
Consider the last pair of formulas, the difference and the sum of the cubes.
As we remember, in the difference of squares, we are multiplying the difference and the sum of these numbers one to another. In the difference of cubes, there are also two brackets.
1 bracket - the sum (or difference) of numbers in the first degree (depending on whether we reveal the difference or the amount of cubes);
2 bracket is an incomplete square (look closely: if we subtracted (or added) the double product of numbers, there would be a square), the sign when multiplying numbers is opposite to the sign of the original expression.
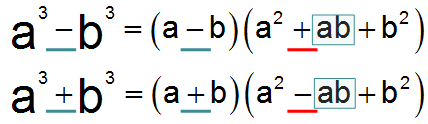
To fix the topic, we will solve several examples:
Compare the resulting expressions:
Training
Tasks:
Answers:
Summarize the final results
There are 7 formulas for abbreviated multiplication:
Do not forget that in the section for the intermediate level of students we have examined the topic "" even deeper.


