Definition Converting a polynomial to the product form of two or more polynomials of nonzero degree is called factoring the polynomial. For example: x2 - a2 \u003d (x - a) (x + a).

Consider various techniques for factoring polynomials.

1) The method of grouping and putting the common factor out of brackets.

When using this method, it is sometimes advisable to apply “artificial” transformations — to break up individual members into similar terms or introduce mutually annihilating members.

Example 1. Factor the polynomial a2 -2bc + 2ac - ab.

Decision. a2 - 2bc + 2ac - ab \u003d (a2 + 2ac) - (2bc + ab) \u003d

A (a + 2s) –b (2s + a) \u003d (a + 2s) (a - b).

Example 2. Factor the polynomial: x2 - 3x + 2.

x2 - 3x + 2 \u003d x2 - x - 2x + 2 \u003d (x2 - x) ‑- (2x - 2) \u003d x (x - 1) - 2 (x - 1) \u003d (x - 1) (x - 2 )

2) The use of formulas of abbreviated multiplication. Using the shortened multiplication formulas, factoring is often greatly facilitated.

Example 3. Factor the polynomial: 5a5x3 + 5a2x9.

Decision. First, take out the common factor 5a2x3, and then apply the formula for the sum of cubes:

5a5x3 + 5a2 x9 \u003d 5a2x3 (a3 + x6) \u003d 5a2x3 (a3 + (x2) 3) \u003d 5a2x3 (a + x2) (a2 - ax2 + x4).

Example 4. Factor the polynomial P (x) \u003d x3 - 3x - 2.

Decision. P (x) \u003d x3 - 3x - 2 \u003d x3 - x - 2x - 2 \u003d (x3 - x) - (2x + 2) \u003d

X (x2 - 1) - 2 (x + 1) \u003d x (x + 1) (x - 1) - 2 (x + 1) \u003d (x + 1) (x2 - x - 2). As,

x2 - x - 2 \u003d x2 - x - 1 - 1 \u003d (x2 - 1) - (x + 1) \u003d (x + 1) (x - 1) - (x + 1) \u003d (x + 1) (x - 2)

then P (x) \u003d (x + 1) 2 (x - 2).

Full square highlighting is sometimes useful.

Example 5. Factor x4 + 4.

x4 + 4 \u003d x4 + 4x2 + 4 - 4x2 \u003d (x2 +2) 2 - (2x) 2 \u003d (x2 + 2x + 2) (x2 - 2x + 2).

For factoring, it turned out to be successful to isolate the full square in the expression x4 + 4 \u003d (x2) 2 + 22 (the formula a2 + b2 \u003d (a + b) 2 - 2ab was used.

3) Factorization of the square trinomial.

ax2 + bx + c \u003d a (x - x0) (x - x2); (a ≠ 0, D \u003d b2 - 4ac≥0), where x1 and x2 are the roots of the trinomial ax2 + bx + s.

4) Factorization of the nth degree polynomial with respect to x.

Polynomial n degree  with respect to x has the form

P (x) \u003d aohp + a1xn-1 + ... + an-1x + an,

where a0 ≠ 0, n ≥ 0 is an integer, a0, a1, ..., an are constants (polynomial coefficients), the letter (value) x can take any numerical values. The polynomial P (x) is written in the standard form in decreasing powers of x.

Two polynomials P (x) and P1 (x) are considered equal: P (x) \u003d P1 (x), if for all values \u200b\u200bof x they take the same values.

Bezout theorem. When dividing the polynomial Pn (x) by the binomial (x-x0), we obtain the remainder R equal to the value of the polynomial at x \u003d x0, i.e. R \u003d Pn (x0).

Pn (x) \u003d (x - x0) Qn-1 (x) + P (x0).

Corollaries from Bezout's theorem:

1. If Pn (x) is divisible by (x - x0) without remainder, ie R \u003d 0, then x \u003d x0 is the root of the polynomial Pn (x), i.e. Pn (x0) \u003d 0.

2. If x \u003d x0 is the root of the polynomial Pn (x), ie Pn (x0) \u003d 0, then Pn (x) is divisible by (x – x0) without remainder, i.e. Pn (x) \u003d (x - x0) Qn-1 (x)).

Summarizing, we get: Pn (x) \u003d a0 (x - x1) (x - x2) ... (x - xn), where x1, x2, ..., xn are the roots of the polynomial.

Example 6. Factor polynomial

P (x) \u003d (x2 + x + 1) (x2 + x + 2) - 12.

P (x) \u003d (x2 + x + 1) ((x2 + x + 1) + 1) - 12 \u003d (x2 + x + 1) 2 + (x2 + x + 1) - 12.

Let x2 + x + 1 \u003d y. Then we have y2 + y - 12 \u003d (y + 4) (y - 3), since the roots of the trinomial y2 + y - 12 are equal to - 4 and 3. Passing from y to x, we get

P (x) \u003d (x2 + x + 5) (x2 + x - 2). Since the trinomial x2 + x - 2 \u003d (x - 1) (x + 2),

then P (x) \u003d (x - 1) (x + 2) (x2 + x + 5).

Mathematics is an interesting science, but sometimes it is quite complicated. Formulas and rules, as well as the multiplication table will help in solving complex problems. In addition, they will provide an opportunity to navigate the question of how to factor prime numbers and polynomials.

How to factor a number

In order to find out the factors of a number, you need to find its smallest divisor. It should be simple and complete. If you record actions, you need to draw a vertical line, dividing the sheet into two columns. Record the original number in the upper left. Now think about what minimum number you can divide this to get an integer without a remainder. Write it down on the left, and the division result on the right. This must be done until the last digit in the column is one. Remember that you cannot divide a number by one. You need to choose from a deuce and above. For example, you need to find the factors of 468. The minimum factor is 2. Write on the left 2, on the right, the division result is 234. Find the divisor of this number. This is also 2. It is necessary to divide 234 by 2. It turns out 117. Write the result in columns. Divide 117. We cannot divide by 2, since it turns out not an integer. Try 3. This number is suitable, write it and the result of division. The answer is 39. What is the minimum number that can be divided by 39? This is also 3. The answer is 13. This number can be divided only by yourself - by 13. It turns out 1. So, you have deduced all the factors of 468. Write them down.

How to factor a number into prime factors

In order to factor the number, you need to know the multiplication table. The fact is that if your number is small, its prime factors are easy to find. For example, you want to calculate the prime factors of the number 10. You need to determine which smallest number you can divide this number, this is 2. We take all the numbers except one. As a result, we get: 2x5 \u003d 10. This means that the numbers 2 and 5, since they are simple, are factors of 10.

How to factor polynomial

In principle, as with primes, there is nothing complicated. The actions are the same, only the number has several members. Before factoring a polynomial, we need to factor out the common factor. For example: 16u in a cube - 24u in a square. Decompose each number into the smallest divisors. What happens: 4u squared * 4u - 4u squared * 6 \u003d 4u squared (4u - 6). This will be the answer.

You can apply a method called "grouping." The principle of operation is the same. You just need to group the polynomials, put out the common bracket. Then find the common factor for each bracket. We also endure it. The numbers in brackets will be the factors of the polynomials. Another way is the “abbreviated multiplication” method. Each polynomial needs to find out the factors and put them in brackets. You need to do this procedure until you reach one.

Consider specific examples of how to factor a polynomial.

The decomposition of polynomials will be carried out in accordance with.

Factor polynomials:

Check if there is a common factor. yes, it is equal to 7cd. Put it out of brackets:

The expression in brackets consists of two terms. The common factor is no longer there, the expression is not a formula for the sum of cubes, which means that the decomposition is completed.

Check if there is a common factor. Not. The polynomial consists of three terms, so we check to see if there is a full square formula. Two terms are the squares of the expressions: 25x² \u003d (5x) ², 9y² \u003d (3y) ², the third term is the double product of these expressions: 2 ∙ 5x ∙ 3y \u003d 30xy. Hence, this polynomial is a full square. Since the double product with a minus sign, this is:

Check if the common factor can be bracketed. There is a common factor, it is equal to a. Put it out of brackets:

In brackets are two terms. Check if there is a formula for the difference of squares or the difference of cubes. a² is the square of a, 1 \u003d 1². Therefore, the expression in brackets can be written according to the formula of the difference of squares:

There is a common factor, it is 5. We take it out of the brackets:

in brackets are three terms. Check if the expression is a full square. Two terms are squares: 16 \u003d 4² and a² is the square of a, the third term is the double product of 4 and a: 2 ∙ 4 ∙ a \u003d 8a. Therefore, it is a full square. Since all terms with a “+” sign, the expression in parentheses is the total square of the sum:

The common factor -2x is taken out of brackets:

In parentheses is the sum of the two terms. Check if the given expression is a sum of cubes. 64 \u003d 4³, x³- cube x. Therefore, the binomial can be decomposed according to the formula:

There is a common factor. But, since the polynomial consists of 4 members, we will first, and only then disregard the common factor. Group the first term with the fourth, the second with the third:

We take out the common factor 4a from the first brackets, and 8b from the second brackets:

There is no common factor yet. To get it, we put the “-” out of the second brackets, and each character in brackets will change to the opposite:

Now we take out the common factor (1-3a):

In the second brackets there is a common factor of 4 (this is the same factor that we did not put out of brackets at the beginning of the example):

Since the polynomial consists of four terms, we perform the grouping. Group the first term with the second, the third with the fourth:

There is no common factor in the first brackets, but there is a formula for the difference of squares, in the second brackets there is a common factor of -5:

There is a common factor (4m-3n). Take it out of brackets.

Factorization of polynomials.

• Training presentation.

• Summary Lesson on Factorization

• 7th grade

Bit of theory

• Factorizing a polynomial means representing it as a product of simpler polynomials.

• There are several ways to decompose:

• Bracketing the common factor

• Grouping Method

• Using Abbreviated Multiplication Formulas

• We use the factorization of the polynomial: 2x2 + x –6 \u003d (2x-3) (x + 2)

• Then the given equation can be rewritten in the form:

• (2x-3) (x + 2) \u003d 0

• The product is zero if one of the factors is zero. Means

• either 2x-3 \u003d 0,

• either x + 2 \u003d 0.

• From the first equation, x \u003d 1.5, and from the second equation, x \u003d -2.

• The equation is solved, it has two roots: 1.5 and –2.

Consider a different situation

• Suppose you need to find the value of a numerical expression

• 532-472

• 612-392

• The most effective solution is to use the square difference formula twice:

• 532-472 = (53-47)(53+47) = 6 100 = 6 = 3

• 612-392 (61-39)(61+39) 22 100 22 11

• Factoring has allowed us to reduce the fraction. Later we will evaluate this also when performing actions with algebraic fractions.

Thus, factorization of the polynomial is used to solve equations, to convert numerical and algebraic expressions. It is applied in other situations, as, say, in the following rather difficult but beautiful example, where the key to success again factorized.

EXAMPLE

• Prove that for any positive integer n  expression n3 +3n2 +2ndivisible by 6.

• Try to solve it

• Let p (n) \u003d n3+ 3n2 +2n.

• If a n\u003d 1 then p(1)= 1 + 3 + 2 \u003d 6. Means p(1) is divisible by 6 without remainder.

• If a n\u003d 2 then p(2)= 23 + 3 · 22 + 2 · 2 \u003d 8 + 12 + 4 \u003d 24. Consequently, and p(2) is divisible by 6 without remainder.

• If a n\u003d 3 then p(3)= 33 + 3 · 32 + 2 · 3 \u003d 27 + 27 + 6 \u003d 60. That's why p(3) is divisible by 6 without remainder.

• But you understand that sorting out so everything  natural numbers we will not succeed. How to be Algebraic methods come to the rescue.

• We have: n3 +3n2 +2n=n(n+1)(n+2).

• Indeed n(n+1)= n2+ n, but ( n2 + n)(n+2)=n3+ 2n2+ n2+ 2n \u003d n3+ 3n2+ 2n.

• So, p (n) \u003d n(n+1)(n+2), i.e. p (n) there is a product of three consecutive natural numbers n, n+1, n+2. But out of three such numbers, one is necessarily divided by 3, which means their product is divided by 3. In addition, at least one of these numbers is even, i.e. divided by 2. So, p (n)divided by 2 and 3, i.e. divided by 6.

• Everything is fine, you say, but how do you know that n3+ 3n2 +2n= n(n+1)(n+2)? The answer is obvious:  you need to learn how to factor polynomials.

• We will pass to this.

Putting the common factor out of brackets Algorithm for finding the common factor of several monomials

• Find the greatest common factor divisor of all monomials in the polynomial - it will be a common numerical factor (of course, this applies only to the case of integer coefficients).

• Find the variables that are included in each member of the polynomial, and choose for each of them the smallest (available) exponent.

• The product of the coefficient found in the first step is a common factor, which is expedient to be taken out of brackets.

ExampleFactor: - x4y3- 2x3y2+ 5x2.

• We will use the formulated algorithm.

• The greatest common factor divisor –1, -2, and 5 is 1.

• Variable x  included in all members of the polynomial with exponents 4, 3, 2, respectively; therefore, can be bracketed x2.

• Variable ynot included in all members of the polynomial; that means it cannot be put out of brackets.

• Output:  can be put out of brackets x2. True, in this case it is more expedient to make - x2. We get:

• -x 4y3- 2x3y2+ 5x2\u003d -x2(x2y3+ 2xy2- 5).

Grouping method To understand the essence of the grouping method, consider the following example: factoring a polynomial xy-6 + 3y-2y

• The first way to group:

• xy-6 + 3y-2y \u003d (xy-6) + (3x-2y).

• Grouping failed.

• The second way of grouping:

• xy-6 + 3y-2y \u003d (xy + 3x) + (- 6-2y) \u003d x (y + 3) -2 (y + 3) \u003d (y + 3) (x-2).

• The third way to group:

• xy-6 + 3y-2y \u003d (xy-2y) + (- 6 + 3x) \u003d y (x-2) +3 (x-2) \u003d (x-2) (y + 3).

• Answer: xy-6 + 3y-2y \u003d (x-2) (y + 3).

• As you can see, the grouping is not always successful the first time. If the grouping turned out to be unsuccessful, discard it, look for another way. As you gain experience, you will quickly find a successful grouping.

Factorization of a polynomial using abbreviated multiplication formulas Remember these formulas:

• a2-b2 \u003d (a-b) (a + b);

• a3-b3 \u003d (a-b) (a2 + ab + b2);

• a3 + b3 \u003d (a + b) (a2-ab + b2);

• a2 + 2ab + b2 \u003d (a + b) 2;

• a2-2ab + b2 \u003d (a-b) 2.

The first of these formulas can be applied to an expression that is square difference  (no matter what - numbers, monomials, polynomials), the second and third - to the expression, which is difference  (or the amount) cubes; the last two formulas apply to the trinomial, which is full square, i.e. containing the sum of the squares of two expressions and the double product of the same expressions.

ExamplesFactor:

• 1) x6-4a4. We use the first formula (difference of squares):

• x6-4a4 \u003d (x3) 2- (2a2) 2 \u003d (x2-2a2) (x3 + 2a2).

• 2) a6 + 27b3.We use the third formula (sum of cubes):

• a6 + 27b3 \u003d (a2) 3+ (3b) 3 \u003d (a2 + 3b) ((a2) 2-a2 · 3b + (3b) 2) \u003d (a2 + 3b) (a4-3a2b + 9b4).

• 3) a2-4ab + 4b2.In this example, a trinomial is given, for its factorization we will use the fifth formula, unless, of course, we make sure that the trinomial is a full square:

• a2-4ab + 4b2 \u003d a2 + (2b) 2-2A2b \u003d (a-2b) 2.

• We made sure that the trinomial contains the sum of the squares of the monomials a  and 2 b, as well as the double product of these monomials. So this is a full square, and the square of the difference.

Factorization of a polynomial using a combination of different techniques

In mathematics, it is not so often that when solving an example, only one technique is used, combined examples are more common, where one technique is used first, then another, etc. In order to successfully solve such examples, it is not enough to know the techniques themselves; one must still be able to develop a plan for their consistent application. In other words, but also experience. These are combined examples we will consider.

Example 1 Factor polynomial 36a6b3-96a4b4 + 64a2b5

1) First, let's take the common factor out of the brackets. Consider the coefficients 36, 96, 64. All of them are divided by 4, and this is the largest common factor, we put it out of the brackets. All members of the polynomial include a variable a  (respectively a6, a4, a2), so you can put it out of brackets a2. Similarly, all members of the polynomial include a variable b  (respectively b3, b4, b5) - can be taken out of brackets b3.

• So, we'll put it out of brackets 4a2b3. Then we get:

• 36a6b3-96a4b4 + 64a2b5 \u003d 4a2b3 (9a4-24a2b + 16b2).

• 2) Consider the trinomial in parentheses: 9a4-24a2b + 16b2. Find out if it is not a full square. We have:

• 9a4-24a2b + 16b2 \u003d (3a2) 2+ (4b) 2-2 · 3a2 · 4b.

• All conditions of the full square are met, therefore,

• 9a4-24a2b + 16b2 \u003d (3a2-4b) 2.

• 3) Combining two tricks (putting the common factor out of brackets and using the formulas of abbreviated multiplication), we get the final result:

• 36a6b3-96a4b4 + 64a2b5 \u003d 4a2b3 (3a2-4b) 2.

Example 2 Factor x4 + x2a2 + a4

• Apply the full square selection method. For this, imagine x2a2  as 2x2a2-x2a2. We get:

• x4 + x2a2 + a4 \u003d x4 + 2x2a2-x2a2 + a4 \u003d

• \u003d (x4 + 2x2a2 + a4) -x2a2 \u003d

• \u003d (x2 + a2) 2- (xa) 2 \u003d (x2 + a2 + xa).

Example 3 Factor n3 + 3n2 + 2n

• First we take advantage of the fact that n  can be put out of brackets: n (n2 + 3n + 2).  Now to the trinomial n2 + 3n + 2  apply the grouping method, having previously presented 3n  as 2n + n. We get:

• n2 + 3n + 2 \u003d n2 + 2n + n + 2 \u003d (n2 + 2n) + (n + 2) \u003d

• \u003d n (n + 2) + (n + 2) \u003d (n + 2) (n + 1).

• Finally we get:

• n2 + 3n + 2 \u003d n (n + 1) (n + 2).

Example 4 Solve the equation x2-6x + 5 \u003d 0

• The first way.  Imagine - 6x  as an amount –X-5x,and then apply the grouping method:

• x2-6x + 5 \u003d x2-5x + 5 \u003d (x2-x) + (- 5x + 5) \u003d x (x-1) -5 (x-1) \u003d (x-1) (x-5).

• Then the given equation will take the form:

• (x-1) (x-5) \u003d 0,

• where do we find that either x \u003d 1or x \u003d 5.

• The second way.  We apply the method of extracting a full square, for which we present term 5 as 9-4. We get:

• x2-6x + 5 \u003d x2-6x + 9-4 \u003d (x2-6x + 9) -4 \u003d

• \u003d (x-3) 2-22 \u003d (x-3-2) (x-3 + 2) \u003d (x-5) (x-1).

• Come to the equation again (x-1) (x-5) \u003d 0,  having roots 1 and 5.

• Answer: 1, 5.

Reduction of algebraic fractions

• Algebraic fraction  called the ratio of two polynomials Pand Q. In this case, use the record P

Identities

• a2-b2 \u003d (a-b) (a + b);

• x2-4x + 4 \u003d (x-2) 2;

• (a + b) c \u003d ac + bc.

• The equalities written are true for any values \u200b\u200bof the variables included in their composition. Such equalities are called identities. The left and right sides of the identity are called expressions, identically equal. Replacing one expression with another identical to it is called identity transformation  expressions.

• Definition   Identity is equality true for any permissible  the values \u200b\u200bof its constituent variables.

MAIN RESULTS

• We have introduced new ones (for you) the concepts  mathematical language:

• factorization of a polynomial;

• algebraic fraction; reduction of algebraic fraction;

• identity, identically equal expressions, identical transformation of expression.

• You met the following methods of factoring the polynomial:

• parenthesis of the common factor;

• grouping;

• the use of formulas of abbreviated multiplication;

• full square selection.

In the general case, this task involves a creative approach, since there is no universal method for solving it. But still try to give a few tips.

In the overwhelming majority of cases, factoring a polynomial is based on the corollary of Bezout's theorem, that is, a root is found or selected and the degree of the polynomial is reduced by unity by dividing by. The root is obtained from the obtained polynomial and the process is repeated until complete decomposition.

If the root cannot be found, then specific decomposition methods are used: from grouping to entering additional mutually exclusive terms.

Further presentation is based on the skills of solving equations of higher degrees with integer coefficients.

Bracketing the common factor.

We start with the simplest case when the free term is equal to zero, that is, the polynomial has the form.

Obviously, the root of such a polynomial is, that is, the polynomial can be represented in the form.

This method is none other than bracketing the common factor.

Example.

Factor a third-degree polynomial.

Decision.

Obviously, that is the root of the polynomial, i.e. x  can be put out of brackets:

Find the roots of the square trinomial

Thus,

Back to top

Factorization of a polynomial with rational roots.

First, we consider the decomposition method of a polynomial with integer coefficients of the form, the coefficient at the highest degree is equal to unity.

In this case, if the polynomial has integer roots, then they are divisors of the free term.

Example.

Decision.

Check if there are whole roots. To do this, we write out the divisors of the number -18 :. That is, if the polynomial has integer roots, then they are among the written numbers. We successively check these numbers according to Horner's scheme. Its convenience is also that in the end we get the expansion coefficients of the polynomial: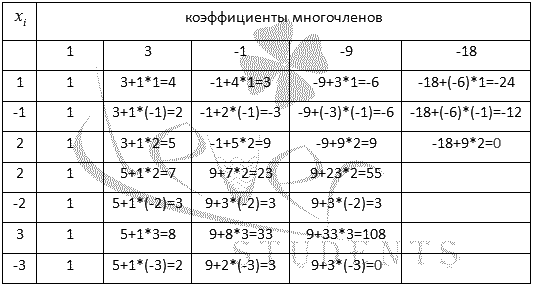

I.e, x \u003d 2  and x \u003d -3  are the roots of the original polynomial and it can be represented as a product:

It remains to expand the square trinomial.

The discriminant of this trinomial is negative, therefore, it has no real roots.

Answer:

Comment:

instead of Horner's scheme, one could use the selection of the root and the subsequent division of the polynomial into a polynomial.

Now we consider the decomposition of a polynomial with integer coefficients of the form, and the coefficient at the highest degree is not equal to unity.

In this case, the polynomial can have fractionally rational roots.

Example.

Factor expression.

Decision.

By replacing a variable y \u003d 2x, we pass to the polynomial with a coefficient equal to unity at the highest degree. To do this, first multiply the expression by 4 .

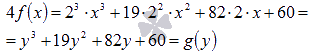
If the resulting function has integer roots, then they are among the divisors of the free term. We write them down:

We compute the values \u200b\u200bof the function sequentially g (y)  at these points until zero.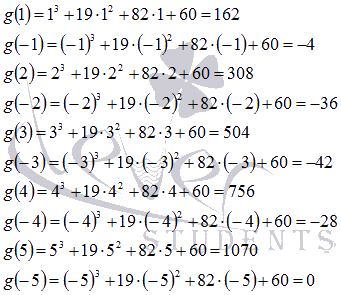

I.e, y \u003d -5  is the root therefore, is the root of the original function. Let us divide the column (corner) of the polynomial into a binomial.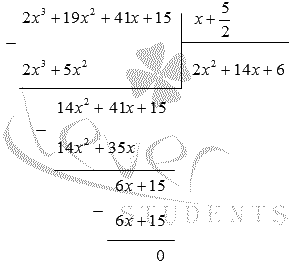

Thus,

It is not practical to continue checking the remaining divisors, since it is easier to factor the resulting square trinomial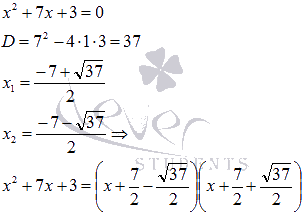

Consequently,

Unknowing polynomial. A theorem on the decomposition of a polynomial in dozens of ignorance. The canonical distribution of the polynomial.