"Methods for solving systems of linear equations" - Equation. Expression. Methods for solving systems of linear equations. Ways to solve. Substitution Method. Number. Solve the system. We will find. Addition method. Solve the system.
"Methods of factoring" - Reduction of algebraic fractions. Solve the equation. Factorization of polynomials. Identities. The main results. Factorization of a polynomial using a combination. Consider a different situation. We use the factorization of the polynomial. The greatest common factor divisor. Factorization of a polynomial using formulas. Imposition common factor beyond the brackets. Factoring is useful.
“Grade 7 Grade” - Solve the equations. Find K. in equality. Imagine as a degree. Calculate. The number 625. Oral score. Present the expression in the form of a degree with a base of 7. Write in the standard form. Degree properties with a natural indicator. The equation with the module. Solve the problem. Number 64. The course of the lesson. Lesson objectives Number 729. Verification work.
“Standard View of the Monomial” - Read the expressions. We use the translational and combinational laws of multiplication. On the desk. The product of numbers. Imagine as a degree. What is called the degree of the monomial. Fastening new material. Exponent. Odds. Fastening. Practical work. Monomial. Fill the table. Computational skills of students. Independent work. Look carefully. Monomial and its standard form.
“Degree properties with a natural indicator” - Epigraph of the lesson. Cases of exponentiation. History. Physical Culture. Biology. Degree properties with a natural indicator. Present the expressions as a degree. Edition Pythagoras. Geography. The material was repeated in the lesson. Gymnastics of the mind.
“Multiplication of Polynomials” Grade 7 ”- Multiply a polynomial by a polynomial. Multiplication of polynomials. Homework. Lesson objectives Polynomial Multiplication Algorithm. Multiplication of a polynomial by a monomial. The rule. Lesson on Multiplication of Polynomials. Work on the task book. Oral work.
summary of other presentations"Methods for solving systems of linear equations" - The equation. Expression. Methods for solving systems of linear equations. Ways to solve. Substitution Method. Number. Solve the system. We will find. Addition method. Solve the system.
"Methods of factoring" - Reduction of algebraic fractions. Solve the equation. Factorization of polynomials. Identities. The main results. Factorization of a polynomial using a combination. Consider a different situation. We use the factorization of the polynomial. The greatest common factor divisor. Factorization of a polynomial using formulas. Bracketing the common factor. Factoring is useful.
"" Degrees "grade 7" - Solve the equations. Find K. in equality. Imagine as a degree. Calculate. The number 625. Oral score. Present the expression in the form of a degree with a base of 7. Write in the standard form. Degree properties with a natural indicator. The equation with the module. Solve the problem. Number 64. The course of the lesson. Lesson objectives Number 729. Verification work.
"Standard view of the monomial" - Read the expressions. We use the translational and combinational laws of multiplication. On the desk. The product of numbers. Imagine as a degree. What is called the degree of the monomial. Fastening new material. Exponent. Odds. Fastening. Practical work. Monomial. Fill the table. Computational skills of students. Independent work. Look carefully. Monomial and its standard form.
“Degree properties with a natural indicator” - Epigraph of the lesson. Cases of exponentiation. History. Physical Culture. Biology. Degree properties with a natural indicator. Present the expressions as a degree. Edition Pythagoras. Geography. The material was repeated in the lesson. Gymnastics of the mind.
"" Multiplication of polynomials "grade 7" - Multiply the polynomial by the polynomial. Multiplication of polynomials. Homework. Lesson objectives Polynomial Multiplication Algorithm. Multiplication of a polynomial by a monomial. The rule. Lesson on Multiplication of Polynomials. Work on the task book. Oral work.
Decision.Based on the properties of the degree, we have:
The correct answer is 4.
A3. Calculate.
| 1. | |
| 2. | 15 |
| 3. | 0,015 |
| 4. | 0,15 |
Decision.Applying the properties of the root, we successively obtain:
.
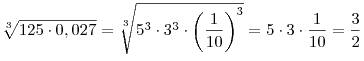The correct answer is: 1.
A4. Find the meaning of the expression.
| 1. | 1 |
| 2. | 2 |
| 3. | 3 |
| 4. | 22 |
Decision.Using the formula for converting the sum of the logarithms into the logarithm of the product, we obtain:
The correct answer is 3.
A5. Find all solutions to the equation 
.
| 1. |
 |
| 2. | |
| 3. |
 |
| 4. |
 |
Decision. Applying the formula 
we get:
The correct answer is 3.
A6. Indicate the gap to which the root of the equation belongs.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision. Solve the equation
.
Thus, the root of the equation belongs to the gap.
The correct answer is: 1.
A7. Solve the inequality.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision. By the property of an exponential function with a base greater than unity
The correct answer is 4.
A8. Determine the number of integer solutions to the inequality.
| 1. | 1 |
| 2. | 2 |
| 3. | 3 |
| 4. | 4 |
Decision. We solve the inequality by the interval method:
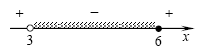
There are three whole solutions in the gap: 4, 5, 6.
The correct answer is 3.
A9. Indicate the gap to which the roots of the equation belong. 
.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision.
I way. Using the equivalence theorem, we obtain:
II method. We reduce the equation to quadratic with respect to:
Thus, the root of the equation belongs to the gap.
The correct answer is 2.
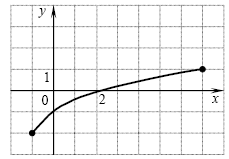A10. The function is set by the schedule. Specify the scope of this function.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision. The scope of a function is the set of values \u200b\u200bof its argument x. In our case, this is a segment.
The correct answer is 4.
A11 Find the scope of the function 
.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision. The domain of definition of a function is given by inequality. We solve it by the interval method:
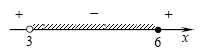
The correct answer is: 1.
A12. Find the many function values.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision.Due to the limited function of the sine and the properties of the inequalities:
The correct answer is: 1.
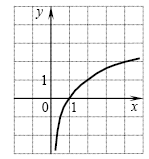A13 The graph of which of the listed functions is shown in the figure?
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision. The figure shows a graph of the function.
The correct answer is 3.
A14. Find the Derived Function 
.
| 1. | |
| 2. |
 |
| 3. |
 |
| 4. |
 |
Decision. Using formulas 
and we get:
The correct answer is: 1.
A15. Find the antiderivative function 
if it is known that.
| 1. | |
| 2. | |
| 3. | |
| 4. |
Decision. We find many antiderivatives:
Will find C:
Thus,
The correct answer is 2.
A16. Find the slope of the tangent drawn to the function graph at its point with the abscissa.
| 1. | 16 |
| 2. | 17 |
| 3. | 0,3 |
| 4. | 0 |
Decision. The angular coefficient of the tangent to the graph of the function at some point is equal to the value of the derivative of the function at this point:
;
The correct answer is 2.
Part B
B1. Let be a solution to the system 
Find the piece.
Decision. Solve the system
Thus, the product of the solutions of the system will be the number 6.
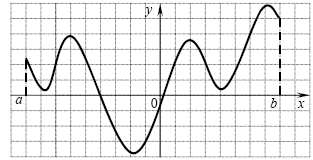B2. The figure shows a graph of the derivative function specified on a segment. Examine the function for monotony and indicate the number of intervals of increase in the answer.
Decision. This function increases at those intervals at which the derivative of this function is non-negative. In our case, there are 2 such intervals.
B3 Find the meaning of the expression.
Decision.
B4. Find the largest integer value of the function 
.
Decision. The highest value of the function y is achieved with the largest value of the radical expression, i.e. at the largest value of the square trinomial on the segment.
.
Answer: 10.5.
B5. Indicate the number of roots of the equation in the gap.
Decision. Simplify the expression:
Solve the system
.
On the gap, the solutions are 0,,,,.
B6. At what value a function 
has a maximum at a point?
Decision. The function has a maximum at the same point as the function, which has a maximum at a point only for negative values \u200b\u200bof the highest coefficient a. Solve the equation
.
B7. To 120 g of a solution containing 80% salt, 480 g of a solution containing 20% \u200b\u200bof the same salt was added. How many percent of salt is contained in the resulting solution?
Decision. In the first solution is grams, and in the second grams of salt. The dry matter mass after draining became 
grams; mass of gram solutions. Then the percentage of salt in the resulting solution is
.
Answer: 32%.
B8 The tenth member of an arithmetic progression is 19, and the sum of the first fifty members is 2500. Find the sum of the third, twelfth, and twentieth members of this progression.
Decision. Since and 
, we have a system
Thus,
The amount sought is equal to
B9. Calculate the volume of a regular triangular pyramid whose height is equal, and all flat angles at the apex are straight.
Decision.
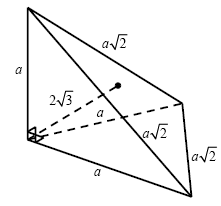1. Let the side edges of the pyramid have a length a. Then the length of the side of its base is equal. If one of the side faces of the pyramid is taken as the base, then the volume of the pyramid is equal (see figure).
2. On the other hand
3. Solving the equation, we find where.
B10 Find the base of an isosceles triangle if the angle at the base is equal, and the point taken inside the triangle is at the same distance, equal to 3, from the sides and at a distance from the base.
Decision.
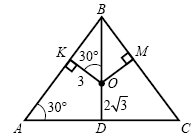1. We introduce the notation as shown in the figure. Since the point O equidistant from the sides, it belongs Bd - the bisector, and, consequently, the median and height of the given triangle.
2. Triangles Abd and Okb - similar ( Bko = Bda \u003d 90 ° and Abd - general), therefore.
Consider a triangle KBO:
consequently,
3. From a right triangle Abd we get
And since,.
Part C
C1. Solve the equation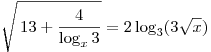 
.
Decision.
.
C2. Find all the values pfor which the equation has no roots.
Decision.
The equation has no solutions for all pnot belonging to the set of values \u200b\u200bof the function that matches the set of values \u200b\u200bof the function on the segment. Find this set:
We have:. (see pic)
a) 
;
b), and, since, we have 
. Since the function is continuous on a segment, its set of values \u200b\u200bis a segment.
Thus, the equation has no solutions for.
C3 A cylinder is described near a regular hexagonal prism. The area of \u200b\u200bthe lateral surface of the cylinder is equal to. The distance between the cylinder axis and the diagonal of the side face of the prism is equal. Find the volume of the prism.
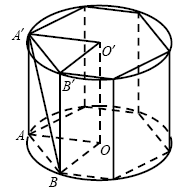Decision. We introduce the notation as shown in the figure.
1. The area of \u200b\u200bthe lateral surface of the cylinder is equal to:
,
where R is the radius of the base of the cylinder, H - his high.
2. The distance between two intersecting lines is equal to the distance between one of the lines and a plane parallel to it, containing the second line. Then the distance between the axis of the cylinder and the diagonal of the side of the prism is the distance from the line to the plane, which is equal to the height of the triangle Aobdrawn from point O.
3. Since the triangle Aob equilateral, its height is 
from where
.
4. The volume of the prism is:
C4. Find all parameter values ain which the domain of definition of the function contains two or three integers.
Decision. According to the meaning of the problem:,.
Since a degree with a fractional positive exponent is defined only for a non-negative basis, the domain of definition of this function is given by inequality. We solve this inequality:
When solving the inequality are all valid values x, and the domain of this function contains an infinite number of integers.
We solve the last inequality with the interval method :.
We have: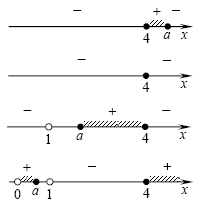 
1. When: OOF - segment.
2. When: OOF - a lot.
3. When: OOF - segment.
4. When: OOF - a lot.
In the first case, OOF contains 2 or 3 integers, if, in the second case, under no a, in the third - with, in the fourth - with no a.