Task 1 with a solution:
The price of a bus ticket is 15 rubles.How many tickets can I buy for 100 rubles after the ticket price is increased by 20%?
Obviously, the solution to this problem must begin with finding a new ticket price. That is, the one that will be established after a price increase of 20%. Find a new ticket price.
1) We find 20% of 15 rubles. By definition, 1% is a hundredth. That is, in order to find 20% of 15 rubles, you need to divide 15 rubles by 100 and multiply by 20. We find: (15: 100) * 20 \u003d 3. Thus, 20% of 15 rubles is 3 rubles.
2) To find a new price - add 3 rubles (equal to 20% of 15 rubles) to the old ticket price of 15 rubles. We get that the new ticket price will be 18 rubles.
3) 100: 18 \u003d 5 (stop 10) - we see that for 100 rubles you can buy 5 tickets
(and 10 rubles - a change that is not enough for another ticket for 18 rubles).
Task 2 with the solution:
A graph is given that shows the air temperature for three days.On one axis (abscissa) is the time of day, on the other (ordinates) - temperature in degrees Celsius.
It is necessary to determine the maximum temperature on August 15th.
Decision:
According to the condition of the problem, it is required to determine the maximum temperature on August 15.
At the first stage, we highlight August 15 on the chart.
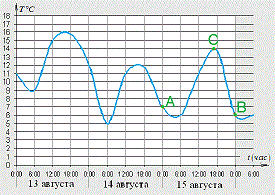
On the chart on August 15, we marked AB.
Obviously, the highest temperature in the interval AB corresponds to the highest temperature during the day.
We marked this value with the letter C. The highest temperature for August 15 is 14 degrees Celsius.
Task 3 with the solution:
The quadrangle depicted on checkered paper is given. Cell size: 1 cm x 1 cm.It is required to find the area of \u200b\u200bthe quadrangle.
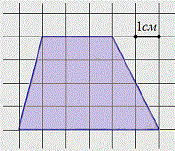
Like any new unknown task, we reduce this to a known one.
Obviously, the figure shows not just a quadrangle, but a trapezoid.
The area of \u200b\u200bthe trapezoid is calculated by the formula:
where h - height a, b - upper and lower bases.
The figure shows that the height of the trapezoid is 4 cm, the upper base 3 cm, and the lower 6 cm. Then, using the above formula, we find:
Thus, the area of \u200b\u200bthe trapezoid is equal to 18 cm 2.
Task 4 with the solution:
The construction company should buy 70 m 3 of foam blocks.There are three providers. Delivery conditions and prices are given in the table.
What amount will be needed for the cheapest purchase with delivery?
| The supplier | The cost of foam blocks (rubles per 1 m 3) | Shipping cost (rub.) | Additional delivery terms |
| 1 | 2600 | 10000 | |
| 2 | 2800 | 8000 | When ordering goods worth more than 150,000 rubles, delivery is free |
| 3 | 2700 | 8000 | When ordering goods worth more than 200,000 rubles, delivery is free |
We determine how much each supplier needs to pay.
1 supplier: 70 * 2600 \u003d 182000, that is, for 70 m 3 of foam blocks you will need to pay 182000 rubles.
The delivery cost is added to this amount: 182000 + 10000 \u003d 192000 rubles.
Thus, the first supplier will need to pay 192,000 rubles.
2 supplier: 70 * 2800 \u003d 196000, that is, for 70 m 3 of foam blocks you will need to pay 196000 rubles.
The additional condition says that upon purchase of goods worth more than 150,000 rubles, delivery is free.
Thus, the second supplier will need to pay 196,000 rubles.
3 supplier: 70 * 2700 \u003d 189000, that is, for 70 m 3 of foam blocks you will need to pay 189000 rubles.
The shipping cost is added to this amount: 189000 + 8000 \u003d 197000 rubles.
Thus, the third supplier will need to pay 197,000 rubles.
It can be seen that the cheapest is to buy foam blocks from the first supplier and this purchase will cost 192,000 rubles.
Answer: 192000
Task 5 with the solution:
Find the root of the equationDecision:
The scheme for solving this and similar equations is simple.
1) Bring the left and right sides of the equation to one base.
2) Solve the equation by equating the indicators of the left and right sides of the equation.
In this case, we notice that. We make the replacement in the original equation:
Then according to item 2) x-2 \u003d 3. This implies that x \u003d 5.
Task 6 with the solution:
In triangle ABC, angle C is equal to 90 degrees, side AB is 5, and the cosine of angle A is 0.8.It is required to find the length of side BC.
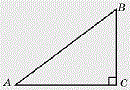
By definition, cosine is the ratio of the adjacent leg to the hypotenuse. That is, cos A \u003d AC / AB. So, 0.8 \u003d AC / 5.
Hence we have: AC \u003d 4. By the Pythagorean theorem, we find BC:.
Thus, BC \u003d 3
Task 7 with the solution:
Find the value of the expression:![]()
Reducing this problem to a known one can be done using the well-known property of logarithms:
according to this formula we have:
Thus, the value of the expression is 3.
Task 8 with the solution:
The figure shows a graph of the function y \u003d f (x), as well as the tangent to the graph at a point with an abscissa equal to 3.Find the value of the derivative of a given function at a point x \u003d 3.
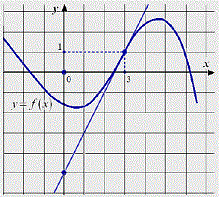
To solve this problem, it is necessary to recall the fact that the derivative of the function at the point is equal to the tangent of the angle formed by the tangent and the axis Ox. I.e, f "(x o) \u003d tg a.

f "(x o) \u003d tg ACD.
Consider the triangle ADC and find tg ACD.By definition, the tangent is equal to the ratio of the opposite leg to the adjacent. AD \u003d 6, CD \u003d 3. Hence it is obvious that tg ACD \u003d 6/3 \u003d 2.Consequently, f "(x o) \u003d 2.
Task 9 with the solution:
The lateral surface area of \u200b\u200bthe cylinder is 16, and the diameter of the base is 4.Find the height of the cylinder.
The area of \u200b\u200bthe lateral surface of the cylinder S side \u003d 2 rh, where r is the radius of the base of the cylinder, h is the height of the cylinder.
Then for our case we write the formula in the form S side \u003d dh, where d is the diameter of the base of the cylinder.
Then we get: h \u003d S side / d. From here we get: h \u003d 16/4
Task 10 with the solution:
There are 36 playing cards. One card is removed at random from the deck.What is the probability that either a trump card or an ace will be drawn. Write down the answer multiplied by 3.
Let event A consist in taking out a trump card, an event
B - the ace is taken out. Then the event A U B is “either the trump card or the ace is taken out”, and the event AB is the “ace of the trump card is taken out”. It is clear that P (A) \u003d 1/4, p (B) \u003d 4/36,
p (AB) \u003d 1/36, therefore, by the formula
P (A U B) \u003d 1/4 + 4/36 - 1/36 \u003d 1/3. 1/3 * 3 \u003d 1. Answer: 1.
Task 11 with the solution:
Two cylinders are given. The volume of the first is 12 m 3.The radius of the base of the second is two times smaller than the first, and the height is three times larger.
It is required to find the volume of the second cylinder.
The volume of the cylinder is calculated by the formula:
Note the radius of the base of the first cylinder rand height h.
Then the radius of the base of the second cylinder is r / 2, and the height 3h.
Substitute in the above formula and get:
Simplify the resulting expression:
Thus, the volume of the second cylinder is 9 m 3.
Task 12 with the solution:
The stone was thrown up vertically.Until it falls, the height at which the stone is located is described by the formula: h (t) \u003d -5t 2 + 18t
(in this case, h is the height in meters, and t is the time in seconds that has passed since the throw).
Determine how much time the stone was at a height of more than 9 meters.
Obviously, the stone may not reach 9 meters,
fly over (and then he will fly the 9 meter mark twice - when it will fly up and when down),
or once - if its flight altitude is exactly 9 meters.
We compose and solve the equation:
In this article we will talk about the difficult tasks of the exam, about the tasks presented in the second part of the exam. About how to learn how to solve them and, if possible, avoid common mistakes.
The first task of the second part of the exam in mathematics (profile)
The first of the most difficult tasks of the exam is an equation or a system of equations. They can be of different types:
- Logarithmic or exponential
- Trigonometric
- Trigonometric for the study of DLD
- Mixed Type Equations
The most common mistakes are a loss of sign, or an error in a formula to bring an equation to a specific form. This, in turn, tells us that, firstly, you need to be VERY careful, and secondly, you need to learn theory. If the loss of a sign leads to an incorrect answer, points will still be added, because The course of the decision was correct. If the student made a mistake in the formula, it is unlikely that the examiner will take pity - they do not like such mistakes.
In more detail about how to prepare for the first task, you can.
The second task of the second part of the exam in mathematics (profile)
This is a stereometry task. Sometimes, it is considered one of the most difficult. Most often, the version does not even have an explanatory drawing that would save a lot of time - you have to draw it yourself. Be careful when transferring a picture to a cleaner - do not confuse the letters and dotted lines with invisible lines - it can be counted as an error and reduce points.
Most often, students fail ignorance of any theory. They either have to derive some necessary regularity from simpler identities, or sign their own powerlessness.
More details about the preparation for the second task of the second part of the exam are written.
The third task of the second part of the exam in mathematics (profile)
In the third task of the second part, students are asked to solve the inequality. It can be one of the following types:
- Rational inequalities
- Irrational inequalities
- Exponential inequalities
- Logarithmic inequalities
- Inequalities with variable base logarithms
- Module Inequalities
- Mixed inequalities
It is important to understand what kind of inequality you have the most difficulty with. According to the experience of our training center, students make the greatest number of mistakes in inequalities with modules. In order to prepare for the third task of the second part of the exam in mathematics, you first need to identify the topic that is most difficult for you and work it out on simpler inequalities, and secondly, to learn how to solve equations under the first number of the second part.
In more detail about preparation for the third task.
The fourth task of the second part of the exam in mathematics (profile)
Here, students are invited to solve the planimetric problem. Significantly more complicated than that given in the sixth task of the first part. On top of that, sometimes in this assignment there are tasks for proving, which, of course, is familiar to students from the OGE, but much more complicated. For more effective preparation, you need, firstly, to learn the theory, and secondly, to solve problems at number six in the first part of the USE options well and quickly.
You can read more about the preparation for 4 (16) assignment of the second part of the exam in mathematics
The fifth task of the second part of the exam in mathematics (profile)
The practical task. Most often with interest. In order to solve such problems, one needs not only a well-developed abstract thinking, but also a relatively high level of erudition, since the authors often use very specific economic terms to formulate tasks. How to learn to solve such problems? Decide as much as possible. By the way, you can go to the bank and talk with the operator about the deposit - interest calculation systems for your hypothetical deposit will be no less complicated than those described in the fifth task of the second part of the exam in mathematics. Here's a kind of free tutor for you on the fifth task!) And of course, ours will help you understand the intricacies of mathematics.
Sixth task of the second part of the exam in mathematics (profile)
Task with a parameter. Here it can be very lucky, or it may not be lucky at all. Unfortunately (or fortunately ..) it is impossible, or almost impossible to “train” a task with a parameter. In any case, not a year before the exam. Cases, of course, are different, but nonetheless. How to prepare - decide more. Do not know how to solve - read the condition, and then the decision. Moreover, you must understand the decision, and be able to reproduce it in, say, a week. Arrange a similar test for yourself, and there is a chance that you will come across about the same task on the exam.
The seventh task of the second part of the exam in mathematics (profile)
Tasks on the properties of numbers. To solve them, you need a well-developed abstract thinking and mathematical instinct. Most often, for the good result of this task, the help of a tutor is needed. Our distance specialists are preparing for the second part of the exam in mathematics and will be happy to help you. The first mini-lesson with us is free, you can send an application in this form:
This article presents an analysis of tasks 9-12 of part 2 of the exam in mathematics of the profile level from a tutor in mathematics and physics. Tutorial video tutorial with analysis of proposed tasks contains detailed and understandable comments for each of them. If you have just started preparing for the exam in mathematics, this article can be very useful for you.
| 9. Find the meaning of the expression |
Using the properties of the logarithms, which you can familiarize yourself with in detail in or in the video tutorial above, we transform the expression:
| 10. A spring pendulum oscillates with a period T \u003d 16 s. Weight of suspended load m \u003d 0.8 kg. The speed of the cargo changes over time in accordance with the formula |
The speed of the cargo 10 s after the start of the oscillatory movement will be equal to:
Then the kinetic energy at this point in time will be equal to:
![]() J.
J.
Let be x - the price of one candy, and y - the price of chocolate. Then 6 candies cost 6 x, and 2% of the value of the chocolate is 0.02 y. Since it is known that 6 candies are cheaper than chocolate by 2%, then the first equation holds: 6 x + 0,02y = yfrom which we obtain that x = 0,98/6 y = 98/600 y = 49/300 y. In turn, 9 candies cost 9 xi.e. 9.49 / 300 y = 49/300 y = 1,47 y. The task is to determine how many percent 1.47 y more than y. If y is 100% then 1.47 y is 1.47 · 100% \u003d 147%. That is 1.47 y more than y by 47%.
| 12. Find the minimum point of the function. |
1) ODZ is given by the inequality: title \u003d "(! LANG: Rendered by QuickLaTeX.com" height="23" width="106" style="vertical-align: -5px;"> (так выражение, стоящее под знаком логарифма, должно быть больше нуля), откуда получаем, что .!}
2) We are looking for a derivative of the function. For a detailed story on how the derivative of this function is calculated, see the video above. The derivative of the function is:
3) We are looking for values xfor which the derivative is 0 or does not exist. It does not exist at, since in this case the denominator vanishes. The derivative is nullified when.
USE in mathematics profile level
The work consists of 19 tasks.
Part 1:
8 tasks with a short answer of a basic difficulty level.
Part 2:
4 tasks with a short answer
7 tasks with a detailed answer of a high level of complexity.
The lead time is 3 hours 55 minutes.
Examples of tests
Decision exams mathematics.
Problem with solution:
In the regular triangular pyramid ABCS with the base ABC, edges are known: AB \u003d 5 roots of 3, SC \u003d 13.
Find the angle formed by the plane of the base and the straight line passing through the middle of the ribs AS and BC.
Decision:
1. Since SABC is a regular pyramid, ABC is an equilateral triangle, and the remaining faces are equal isosceles triangles.
That is, all sides of the base are 5 sqrt (3), and all side edges are 13.
2. Let D be the midpoint of BC, E the midpoint of AS, SH the height lowered from point S to the base of the pyramid, EP the height lowered from point E to the base of the pyramid.
3. Find AD from the right-angled triangle CAD by the Pythagorean theorem. It turns out 15/2 \u003d 7.5.
4. Since the pyramid is correct, the point H is the intersection point of the heights / medians / bisectors of the triangle ABC, which means that it divides AD in the ratio 2: 1 (AH \u003d 2 AD).
5. Find SH from the right triangle ASH. AH \u003d AD 2/3 \u003d 5, AS \u003d 13, by the Pythagorean theorem SH \u003d sqrt (13 2 -5 2) \u003d 12.
6. The triangles AEP and ASH are both rectangular and have a common angle A, therefore, similar. By condition, AE \u003d AS / 2, which means that AP \u003d AH / 2 and EP \u003d SH / 2.
7. It remains to consider the right triangle EDP (we are just interested in the angle EDP).
EP \u003d SH / 2 \u003d 6;
DP \u003d AD 2/3 \u003d 5;
Angle tangent EDP \u003d EP / DP \u003d 6/5,
EDP \u200b\u200bAngle \u003d arctg (6/5)
Answer:
Do you know that?
Among all the figures, with the same perimeter, the circle will have the largest area. And vice versa, among all the figures with the same area, the circle will have the smallest perimeter.
Leonardo da Vinci deduced a rule according to which the square of the diameter of a tree trunk equal to the sum squares of branch diameters taken at a common fixed height. Later studies confirmed it with only one difference - the degree in the formula does not necessarily equal 2, but lies in the range from 1.8 to 2.3. It was traditionally believed that this pattern is explained by the fact that a tree with such a structure has an optimal mechanism for supplying branches with nutrients. However, in 2010, the American physicist Christoph Eloy found a simpler mechanical explanation for the phenomenon: if we consider a tree as a fractal, then Leonardo's law minimizes the probability of breaking branches under the influence of wind.
Laboratory studies have shown that bees can choose the best route. After localization of the flowers arranged in different places, the bee flies and comes back in such a way that the final path is the shortest. Thus, these insects effectively cope with the classic “salesman problem” from computer science, which modern computers, depending on the number of points, can spend more than one day to solve.
If you multiply your age by 7, then multiply by 1443, the result will be your age written three times in a row.
We consider negative numbers to be something natural, but this was not always the case. For the first time, negative numbers were legalized in China in the III century, but were used only for exceptional cases, as they were considered, in general, meaningless. A little later, negative numbers began to be used in India to denote debts, but to the west they did not take root - the famous Diophantus of Alexandria argued that the equation 4x + 20 \u003d 0 is absurd.
The American mathematician George Danzig, being a graduate student at the university, was once late for a lesson and accepted the equations written on the board for his homework. It seemed to him more complicated than usual, but after a few days he was able to complete it. It turned out that he solved two "unsolvable" problems in statistics, over which many scientists fought.
In Russian mathematical literature, zero is not a natural number, but in Western literature, on the contrary, it belongs to the set of natural numbers.
The decimal number system used by us arose due to the fact that a person has 10 fingers on his hands. The ability to abstract counting appeared in people not immediately, but it was the most convenient to use fingers precisely for counting. Maya civilization and independently of them the Chukchi historically used the twenty-decimal number system, using fingers not only of hands, but also of feet. The basis of the duodecimal and hexadecimal systems, common in ancient Sumer and Babylon, was also the use of hands: the phalanges of the other fingers of the palm, the number of which is 12, were counted with the thumb.
One lady friend asked Einstein to call her, but warned that her phone number was very difficult to remember: - 24-361. Do you remember? Repeat! Surprised Einstein replied: “Of course I did!” Two dozen and 19 squared.
Stephen Hawking is one of the largest theoretical physicists and a popularizer of science. In a story about himself, Hawking mentioned that he had become a professor of mathematics without receiving any mathematical education since high school. When Hawking began teaching mathematics at Oxford, he read a textbook, two weeks ahead of his own students.
The maximum number that can be written in Roman numerals without violating the Schwartzman rules (rules for writing Roman numerals) is 3999 (MMMCMXCIX) - you cannot write more than three digits in a row.
There are many parables about how one person offers another to pay him for a certain service in the following way: he puts one rice grain on the first square of the chessboard, two on the second and so on: twice as much on each next cell as on the previous one. As a result, one who pays in this way will certainly go broke. This is not surprising: it is estimated that the total weight of rice will be more than 460 billion tons.
In many sources, often with the aim of encouraging poorly performing students, there is a statement that Einstein failed mathematics at school or, moreover, did poorly in all subjects. In fact, this was not so: Albert at a young age began to show talent in mathematics and knew it far beyond the school curriculum.


