Theorem 1 The angle with a vertex inside the circle is measured by the half-sum of the arcs on which the given angle and the vertical angle with it are based. Evidence. Consider the angle of the ACB with the vertex C inside the circle and points A and B on the circle. Let A1, B1 be the points of intersection with the circle of the sides of the angle vertical to it. Draw the chord BB 1. The angle ACB is the external angle of the triangle B 1 CB. Consequently, ACB \u003d AB 1 B + B 1 BA 1. The angles on the right side of the equality are measured by the halves of the corresponding arcs, which completes the proof.
Theorem 2 The angle between a tangent to a circle and a chord drawn through a point of tangency is measured by half the arc of a circle enclosed inside this angle. Evidence. Let the angle ACB be formed by the tangent AC and the chord BC of the circle. If this angle is a straight line, then BC is the diameter of the circle and, therefore, the angle ACB is measured by half of the arc of the semicircle enclosed inside this angle. If the angle ACB is sharp, then draw a diameter CD. We have ACB \u003d ACD - BCD. The ACD angle is measured in half the circular arc CBD. The angle of the BCD is measured by half the arc of the BD circle. Therefore, their difference (angle ACB) is measured by half the arc CB of a circle enclosed within this angle. Independently consider the case of an obtuse angle.
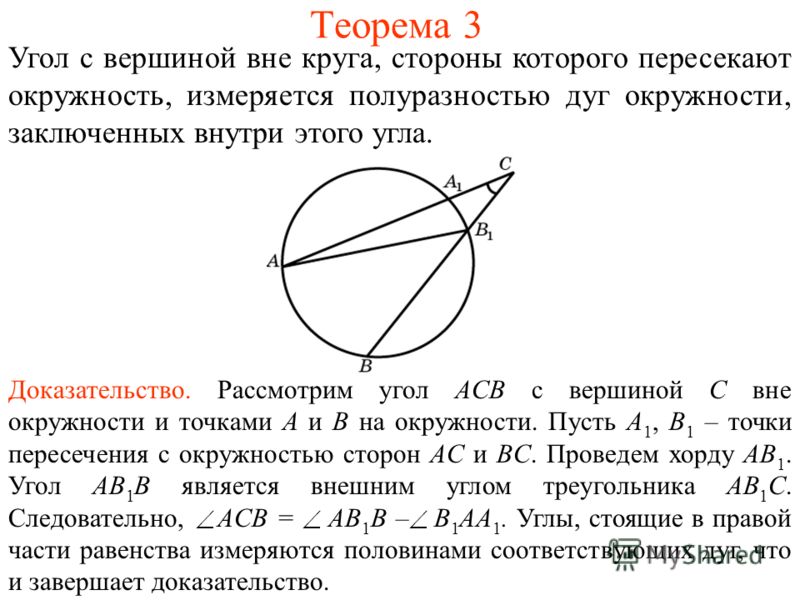
Theorem 3 An angle with a vertex outside a circle whose sides intersect a circle is measured by the half-difference of the arcs of a circle enclosed within this angle. Evidence. Consider the angle ACB with vertex C outside the circle and points A and B on the circle. Let A1, B1 be the intersection points with the circle of sides AC and BC. Draw the chord AB 1. The angle AB 1 B is the external angle of the triangle AB 1 C. Consequently, ACB \u003d AB 1 B - B 1 AA 1. The angles on the right side of the equality are measured in half of the corresponding arcs, which completes the proof.
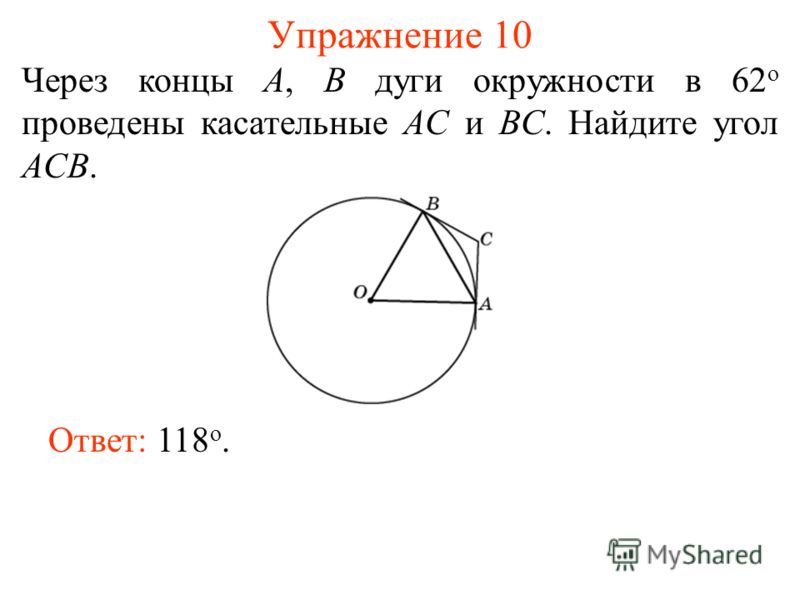
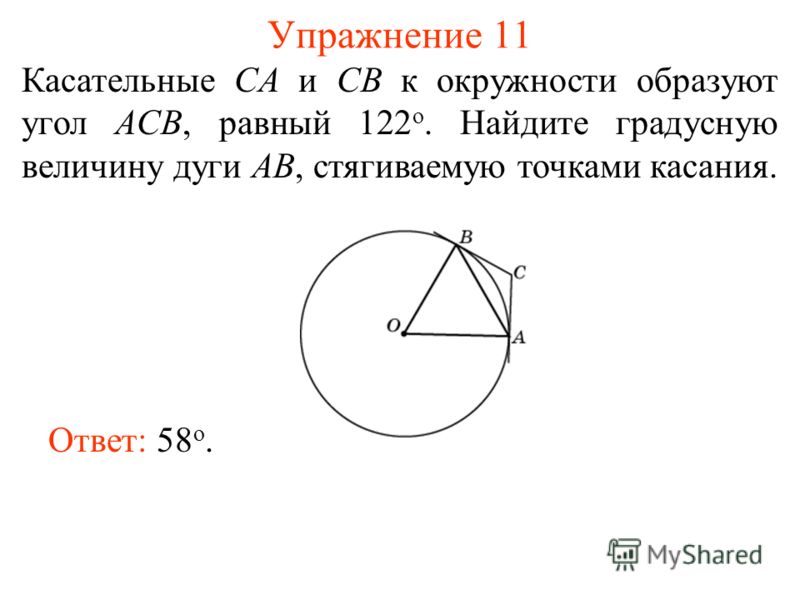
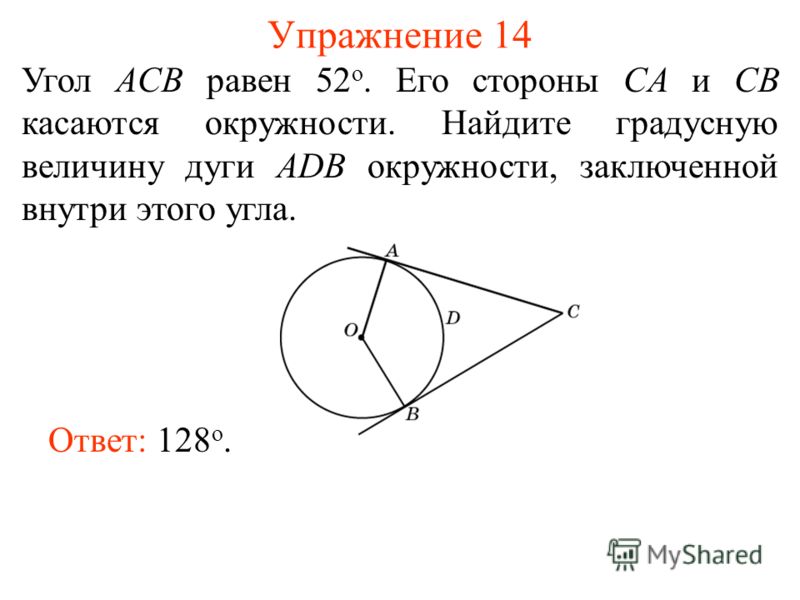
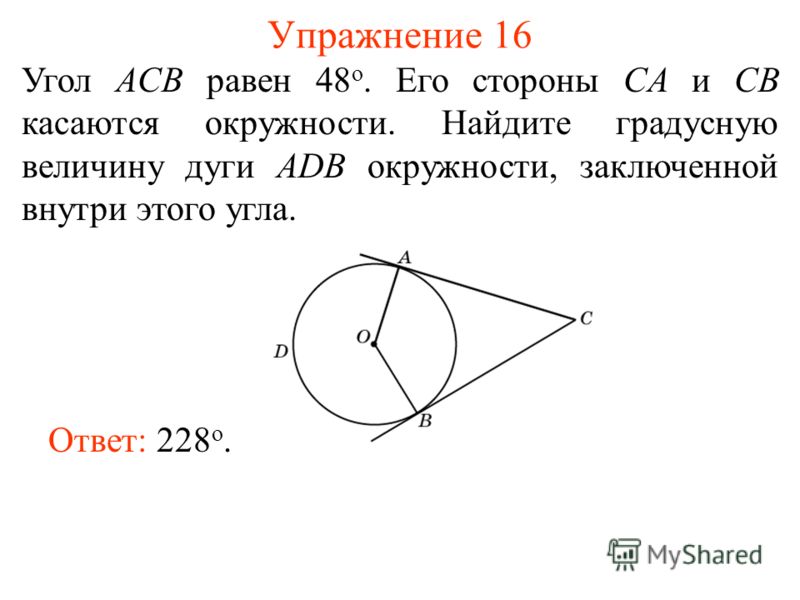
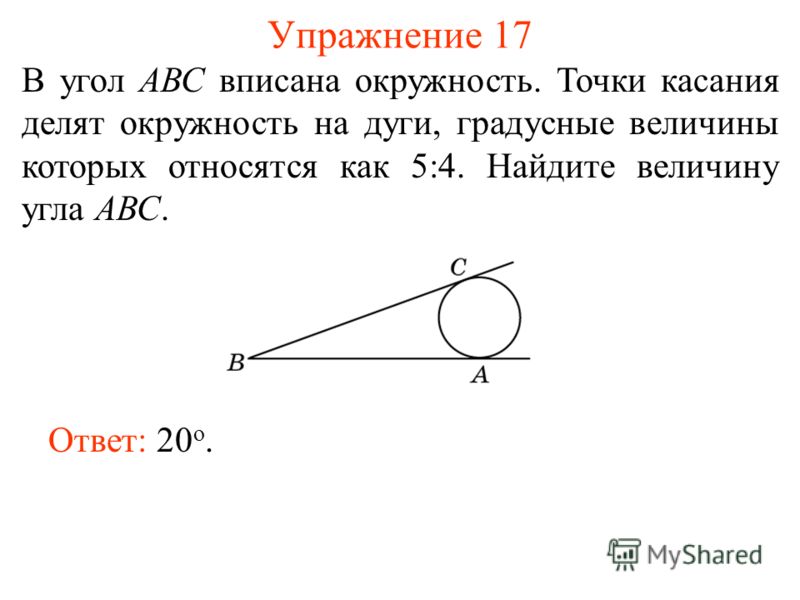
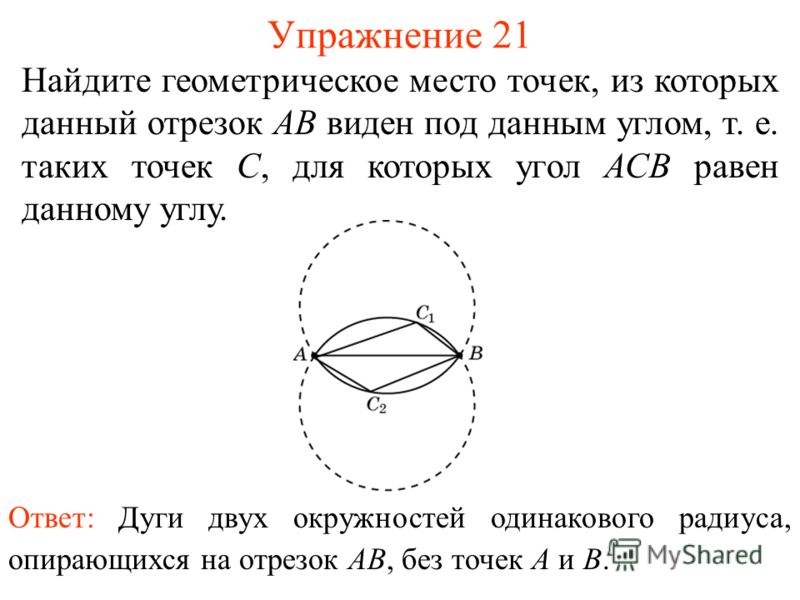
Exercise 21 Find the locus of the points from which a given segment AB is visible at a given angle, that is, such points C for which the ACB angle is equal to this angle. Answer: Arcs of two circles of the same radius, based on the segment AB, without points A and B.
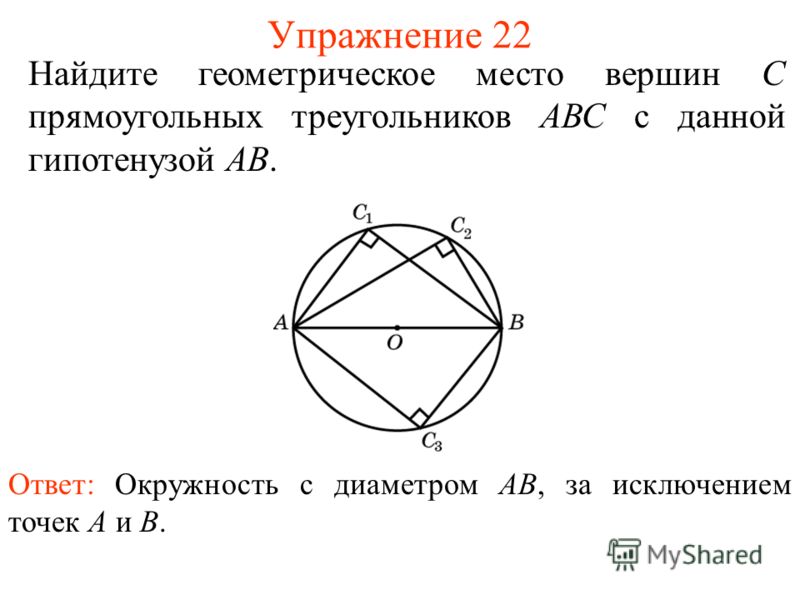
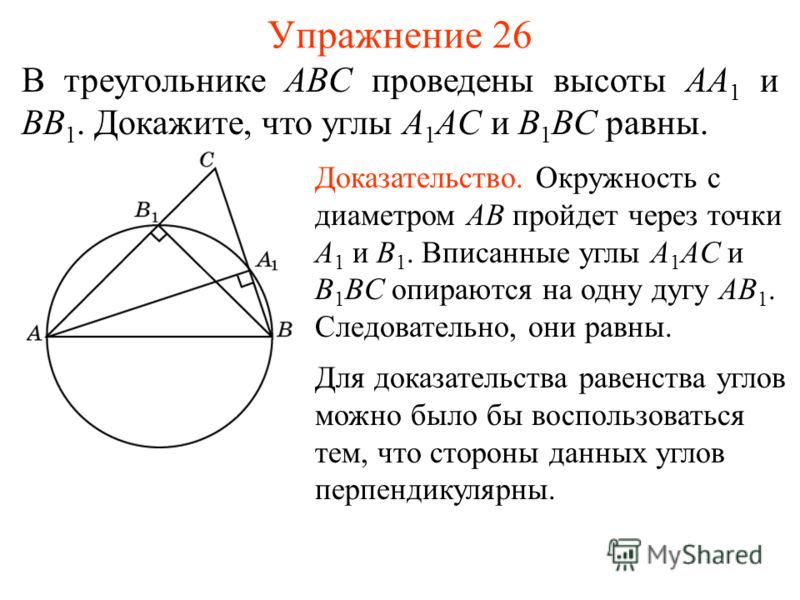
Exercise 23 Answer: a) Т Т Т lying outside a circle with a diameter AB and not belonging to a straight line AB; For the given points A and B, find the geometrical location of the points C for which the ASB angle is: a) acute; b) stupid. b) HMT lying inside a circle with a diameter AB and not belonging to the segment AB. Exercise 26 In the triangle ABC, the heights AA 1 and BB 1 are drawn. Prove that the angles A 1 AC and B 1 BC are equal. Evidence. A circle with diameter AB passes through points A 1 and B 1. The inscribed angles A 1 AC and B 1 BC are based on the same arc AB 1. Therefore, they are equal. To prove the equality of angles, we could use the fact that the sides of these angles are perpendicular.
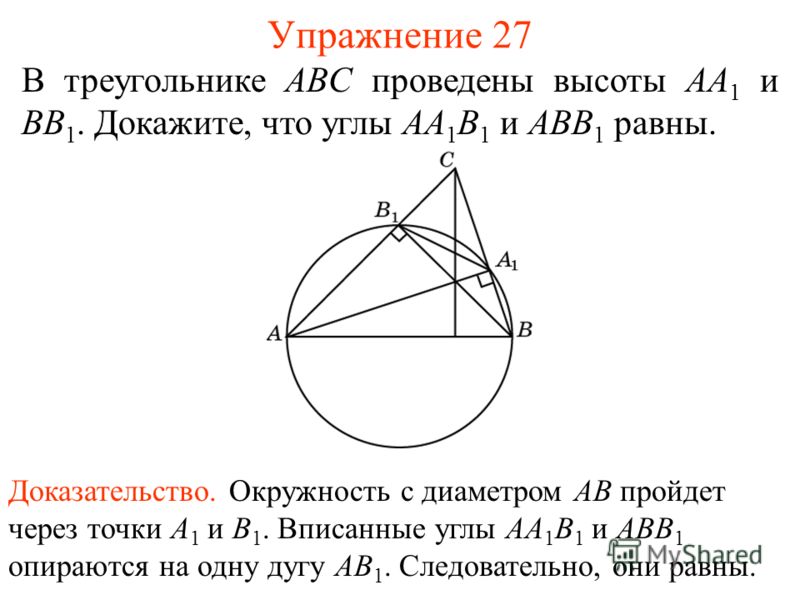
Exercise 27 The heights AA 1 and BB 1 are drawn in triangle ABC. Prove that the angles AA 1 B 1 and ABB 1 are equal. Evidence. A circle with a diameter AB passes through points A 1 and B 1. The inscribed angles AA 1 B 1 and ABB 1 are based on the same arc AB 1. Therefore, they are equal.
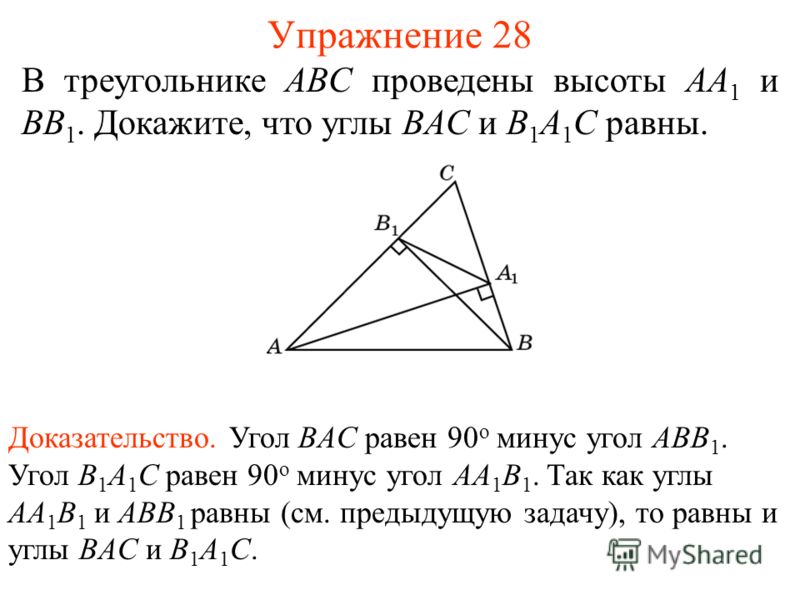
Exercise 28 In triangle ABC, the heights AA 1 and BB 1 are drawn. Prove that the angles BAC and B 1 A 1 C are equal. Evidence. The angle BAC is 90 ° minus the angle ABB 1. The angle B 1 A 1 C is 90 ° minus the angle AA 1 B 1. Since the angles AA 1 B 1 and ABB 1 are equal (see the previous task), the angles BAC and B 1 A 1 C.
The main theorems
Definition 1 . The angular value of an arc is the ratio of the length of this arc to the circumference times 2π.
Theorem 1 . The magnitude of the central angle is equal to the angular magnitude of the arc on which it rests.
Theorem 2
. The value of the inscribed angle is equal to half the angular value of the arc on which it rests.
Consequence. The inscribed angles based on the same arc or on equal arcs of the same circle are equal.
Theorem 3 . The angle between the tangent and the chord extending from one point of the circle is measured by half the angular value of the arc enclosed inside this angle (Fig. 1).
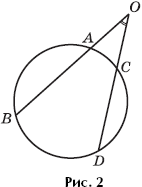
Theorem 4 . The angle, the vertex of which is located outside the circle, is measured by the half-difference of the angular values \u200b\u200bof the arcs of the circle of this circle, enclosed inside the angle (Fig. 2).
Theorem 5
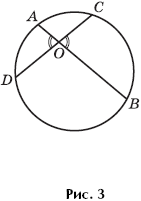
The angle, the vertex of which is located inside the circle, is measured by the half-sum of the angular values \u200b\u200bof the arcs, which are cut from the circle circumference of the side of the angle and their continuation (Fig. 3).
Theorem 6 The sum of the opposite angles of a quadrilateral inscribed in a circle is π, and vice versa, if the sum of the opposite angles of a convex quadrilateral is π, then a circle can be described around this quadrilateral.
Theorem 7 The products of the lengths of the segments of two intersecting chords are equal (see Fig. 3).
Theorem 8
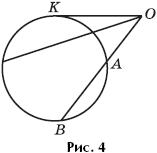
. The product of the length of the section secant and the length of its outer part is a constant, and it is equal to the square of the length of the tangent drawn to the circle from the same point (Fig. 4).
Proofs of some theorems
Proof of Theorem 4 . We first consider the case where the rays forming a given angle intersect each circle at two different points (Fig. 5).
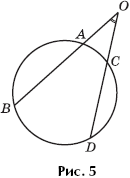
Denote by O the vertex of the angle, and the intersection points of the rays and the circle by A, B, C and D (A between O and B, C between O and D). Then
The first equality is true, since in the triangle OBC the external angle is BCD equal to the sum two internal corners, not adjacent to it.
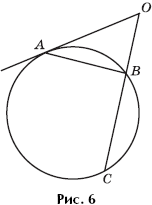
Now let one of the rays (for example, OA) touch the circle at point A, and the other intersect it at points B and C; B between O and C (Fig. 6).
Finally, let both the rays OA and OB touch the circle at points A and B (Fig. 7).
Then the triangle OAB is isosceles, and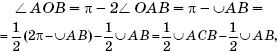 
where the arc ACB is the largest of the circular arcs enclosed between points A and B.
Proof of Theorem 5 . Let the chords AB and CD of the circle intersect at the point O (Fig. 8). Since in the triangle OBD the external angle AOD is the sum of the two internal angles that are not adjacent to it, then
Proof of Theorem 8.
We first prove the first part of the theorem. Let OB and OD be two secant to the circle, and OA and OC their outer parts, respectively. Since the angles ABC and ADC are equal (as inscribed, leaning on the same arc), the triangles AOD and BOC are similar (in two angles). Consequently,
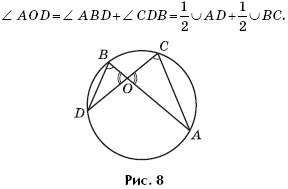
Now let OK be the tangent to the circle and OB the secant (OA is its outer part) (Fig. 9).
Since the angle OKA is equal to half the angular value of the arc KA (as the angle between the tangent and the chord), and the angle KBA is equal to half the angular value of the arc KA (as inscribed, leaning on this arc), ∠OKA \u003d ∠KBA, and the triangle OKA is similar to a triangle KOB (two angles). We have: 
Task solutions
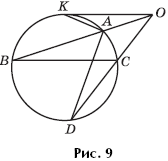
Task 1 A regular triangle ABC with a side equal to 3 is inscribed in a circle. Point D lies on a circle, and the length of the chord AD is equal (Fig. 10). Find the lengths of the chords BD and CD.
Decision.
It is easy to see that the radius of a circle described near a regular triangle with side ais equal
well, the radius of this circle is equal. Let O be the center of a given circle. In the AOD triangle, all sides are equal. Therefore, ∠DAO \u003d 60 °. In addition, since the triangle ABC is regular, ∠OAC \u003d 30 °.
Therefore, ∠DAC \u003d 90 °, and the triangle DAC is rectangular. Therefore, CD is the diameter of the circle, and 
Therefore, the triangle BCD is right-angled, whence, by the Pythagorean theorem, we find that Clearly, when we re-designate points B and C, we get that
Answer: and
Task 2 . A circle of radius R passes through the vertices A and B of triangle ABC and touches the line AC at point A (Fig. 11). Find the area of \u200b\u200btriangle ABC, knowing that ∠ABC \u003d β, ∠CAB \u003d α.
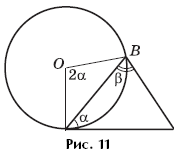
Decision. The angle α between the tangent AC and the chord AB extending from the point A of the circle is equal to half the angular value of the arc AB and, therefore, is equal to any inscribed angle based on the same arc. Therefore, we can apply the sine theorem: AB \u003d 2Rsin α.
Consider the triangle ABC, to which the sine theorem also applies: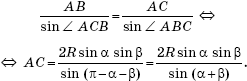 
Consequently,
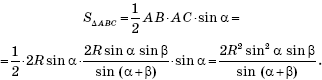
Answer: 
Task 3 . A circle is described around triangle ABC. The median AD is continued until it intersects with this circle at point E (Fig. 12). It is known that AB + AD \u003d DE, the angle BAD is 60 ° and AE \u003d 6. Find the area of \u200b\u200bthe triangle ABC.
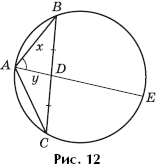
Decision. Let AB \u003d x, AD \u003d y, then, according to the condition of the problem, DE \u003d x + y. Since in the circle the products of the segments of two intersecting chords are equal, we have:
AD ∙ DE \u003d BD ∙ DC ⇔
We apply the cosine theorem to triangle ABD:
BD2 \u003d AB2 + AD2 - 2AB ∙ AD ∙ cos ∠BAD ⇔
⇔
⇔ x2 \u003d 2xy ⇔ x \u003d 2y.
Condition AE \u003d 6 gives the equality x + 2y \u003d 6. Substituting x \u003d 2y into it, we find: x \u003d 3. The desired area is
Answer:
Task 4
. On the side AC of the acute-angled triangle ABC, the point D is taken so that AD \u003d 1,
DC \u003d 2 and BD is the height of the triangle ABC. A circle of radius 2 passing through points A and D touches at point D the circle circumscribed near triangle BDC (Fig. 13). Find the area of \u200b\u200btriangle ABC.
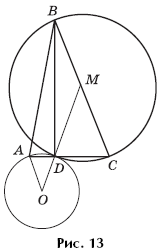
Decision. The triangle BCD is rectangular, therefore the center of the circle circumscribed around it is the midpoint M of the side BC. Let O be the center of a circle of radius 2 passing through A and D. Since these circles are tangent, the points O, D, M lie on one straight line. And from the equality of the angles of ADO and CDM, due to the isosceles of the triangles ADO and CDM, the similarity of these triangles follows. Therefore, DM \u003d 4 and BC \u003d 2 DM \u003d 8. Applying the Pythagorean theorem to the triangle BCD, we obtain that Therefore, 
Answer:
Task 5
. A triangle ABC is given in which
BC \u003d 5. The circle passes through the vertices B and C and intersects the side AC at the point K so that
CK \u003d 3, KA \u003d 1. It is known that the cosine of the angle ACB is equal (Fig. 14). Find the ratio of the radius of a given circle to the radius of a circle inscribed in triangle ABK.
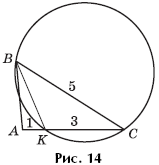
Decision. We apply the cosine theorem to triangle ABC:
AB2 \u003d BC2 + AC2 - 2BC ∙ AC ∙ cos ∠ACB \u003d 9 ⇒
⇒ AB \u003d 3.
Therefore, the triangle ABC is right-angled (since its sides are 3, 4, 5). The triangle ABK is also rectangular, applying the Pythagorean theorem to it, we obtain that, therefore, the radius of the circle inscribed in the triangle ABK is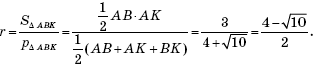 
The article was published with the support of the training center "NP MAEB" in St. Petersburg. Organization of work of the labor protection and industrial safety service, training of professionals in this field. Fire-technical minimum programs for managers and specialists, slingers, lifters, lift drivers, workers working with cylinders with liquefied petroleum gases, etc. You can find out more about the center, prices, contacts and leave a request on the website located at: http://www.maeb.ru/.
The circle given in the condition of the problem is described near the triangle BCK. By the sine theorem, its radius is
Then the desired ratio is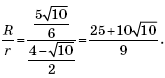 
Task 6
. The sides AB \u003d 6, BC \u003d 4, AC \u003d 8 are known in triangle ABC. The bisector of angle C
intersects side AB at point D. Through points A, D, C, a circle is drawn intersecting side BC at point E (Fig. 15). Find the area of \u200b\u200bthe triangle ADE.
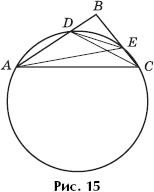
Decision. The bisector CD of the angle ACB divides the side AB into segments proportional to the adjacent sides, therefore AD \u003d 4 and BD \u003d 2. Further, the angles DAE and DCE are equal, as they rely on the same arc, and the angles AED and ACD are similarly equal. But ∠ACD \u003d ∠DCE, therefore all four named angles are equal. Therefore, the triangle ADE is isosceles and DE \u003d 4.
Find the sine of the angle ADE. Since the quadrilateral ADEC is inscribed in a circle, then
∠ADE + ∠ACE \u003d 180 °, sin ∠ADE \u003d sin ∠ACE.
We apply the cosine theorem to triangle ABC: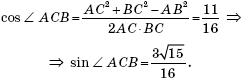 
Means
Answer:
Task 7 . Around the triangle ABC with sides AC \u003d 20 and an angle B equal to 45 °, a circle is described. A tangent to a circle is drawn through point C, intersecting the extension of side AB beyond point A at point D (Fig. 16). Find the area of \u200b\u200bthe triangle BCD.
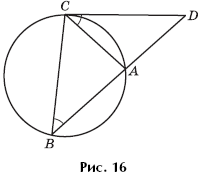
Decision. The angle ABC is equal to half the angular magnitude of the arc AC, as an inscribed angle based on this arc. The angle ACD is also equal to half the angular magnitude of the arc AC, as the angle between the tangent and the chord. Therefore, these angles are equal, and the triangles DBC and DCA are similar in two angles. The areas of these triangles are referred to as the squared similarity coefficient. Find this coefficient, it is equal to BC: AC. Let BC \u003d 10x, then, applying the cosine theorem to triangle ABC, we obtain:
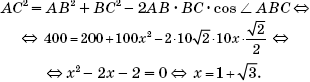
Means 
therefore 
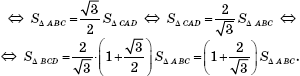
Easy to compute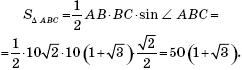 
Answer:
Task 8 . A quadrangle is inscribed in a circle of radius 17, the diagonals of which are mutually perpendicular and are at a distance of 8 and 9 from the center of the circle (Fig. 17). Find the lengths of the sides of the quadrangle.
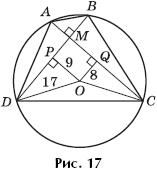
Decision. We denote the original quadrangle by ABCD so that point B lies on the smaller arc AC, and point A lies on the smaller arc BD. Let O be the center of the circle, OQ and OP be the perpendiculars dropped from the center of the circle to the chords AC and BD, respectively, M be the intersection point of AC and BD. Then AQ \u003d QC, BP \u200b\u200b\u003d PD, OQMP is a rectangle with sides OQ \u003d PM \u003d 8 and
OP \u003d QM \u003d 9. We apply the Pythagorean theorem to the triangle COQ:
Similarly, from the triangle ODP we get that 
Means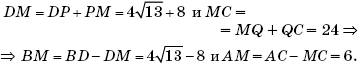 
We find the sides of the quadrangle ABCD, using the Pythagorean theorem:
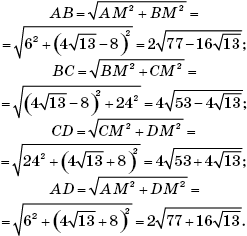
Answer:
Task 9
. The pentagon ABCDE is inscribed in a circle of unit radius (Fig. 18).
It is known that BC \u003d CD. What is the area of \u200b\u200bthe pentagon?
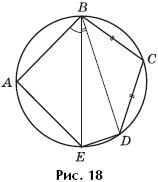
Decision. Let O be the center of a given circle. Since the sides of the triangle AOB are 1, 1, then this triangle is rectangular, and the angle AOB is equal. Since the angle ABE is equal, the angle AOE is also equal, and BE is the diameter of the circle. The angle EBD is therefore equal, the angle EOD is equal to, and since BC \u003d CD, then 
So, the pentagon ABCDE consists of two right-angled and three equilateral triangles. Its area is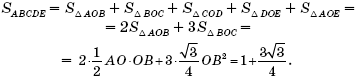 
Answer:
Task 10 . The convex quadrangle ABCD is inscribed in a circle. The diagonal AC is the bisector of the angle BAD and intersects the diagonal BD at the point K (Fig. 19). Find the length of the segment KC if BC \u003d 4 and AK \u003d 6.
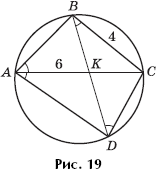
Decision. Since AC is the bisector of the angle BAD, the angle BAC is equal to the angle CAD. On the other hand, the angles of CAD and CBD are equal (as inscribed, relying on the same arc). So the angle BAC is equal to the angle CBK. Therefore, the triangle ABC is similar to the triangle BCK (two angles). We have:
Answer: 2.
Tasks for an independent solution
C-1. In triangle ABC we have: AB \u003d 20, AC \u003d 24. It is known that the vertex C, the center of the circle inscribed in triangle ABC, and the intersection point of the bisector of angle A with side BC lie on a circle whose center is on side AC. Find the radius of the circle circumscribed around the triangle ABC.
C-2. Given a right triangle ABC with a right angle at the vertex C. The angle CAB is α. The bisector of angle ABC intersects the side of AC at point K. On side BC, a circle is constructed on diameter BC that intersects hypotenuse AB at point M. Find the angle AMK.
C-3. Two intersecting circles are given on the plane. The first has a center at O1 and a radius equal to 4, the second has a center at O2 and a radius equal to Line O1 O2 intersects both circles, and the angle KO1 O2 is 30 ° (where K is one of the intersection points of the circles). The vertex A of the equilateral triangle ABC is the intersection point of the second circle and the segment O1 O2, and the side BC is the chord of the first circle perpendicular to the line O1 O2. Find the area of \u200b\u200btriangle ABC, if it is known that AB< 4.
C-4. A quadrangle ABCD is inscribed in a circle whose diagonals are mutually perpendicular and intersect at point E. A line passing through point E and perpendicular to AB intersects side CD at point M. Prove that EM is the median of triangle CED and find its length if AD \u003d 8, AB \u003d 4, and ∠CDB \u003d α.
C-5. The trapezoid ABCD is inscribed in a circle (BC C AD). On the CD arc, point E is taken and connected to all the vertices of the trapezoid. In addition, it is known that ∠CED \u003d 120 ° and ∠ABE - ∠BAE \u003d α. For triangle ABE, find the ratio of the perimeter to the radius of the inscribed circle.
C-6. In triangle ABC it is known that BC \u003d 4. In addition, the center of the circle drawn through the midpoints of the sides of the triangle lies on the bisector of angle C. Find AC.
C-7. In triangle ABC on points AB and AC, points B1 and C1 are selected, respectively, so that AB1: AB \u003d 1: 3 and AC1: AC \u003d 1: 2. A circle is drawn through points A, B1 and C1. A line is drawn through point B1 intersecting the segment AC1 at point D, and a circle at point E.
Find the area of \u200b\u200btriangle B1 C1 E if AC1 \u003d 4, AD \u003d 1, DE \u003d 2, and the area of \u200b\u200btriangle ABC is 12.
S-8. The diagonals of the quadrangle ABCD inscribed in a circle intersect at point E. On line AC, point M is taken, with ∠DME \u003d 80 °, ∠ABD \u003d 60 °, ∠CBD \u003d 70 °. Where is the point M: on the diagonal or on its continuation? Justify the answer.
S-9. Through the center of the circle described near the triangle ABC, straight lines are drawn perpendicular to the sides AC and BC. These lines intersect the height CH of the triangle or its extension at points P and Q. It is known that CP \u003d p, CQ \u003d q. Find the radius of the circle circumscribed around the triangle ABC.
S-10. On the side AB of the triangle ABC as on the diameter, a circle is constructed intersecting the sides AC and BC at points D and E, respectively. Line DE divides the area of \u200b\u200btriangle ABC in half and forms an angle of 15 ° with line AB. Find the angles of triangle ABC.
S-11. The circle touches the sides of the corner with vertex O at points A and B. On this circle inside the triangle AOB, point C is taken. The distances from point C to the lines OA and OB are equal to a and b, respectively. Find the distance from point C to the chord AB.
S-12. In the trapezoid ABCD with the bases AD and BC, the diagonals AC and BD intersect at point E. A circle is described around the triangle ECB, and a tangent to this circle drawn at point E intersects the line AD at point F so that points A, D and F lie sequentially on this line. It is known that AF \u003d a, AD \u003d b. Find EF.
S-13. In the quadrangle ABCD, the diagonals AC and BD are perpendicular and intersect at point P. The length of the segment connecting the vertex C to the point M, which is the middle of the segment AD, is equal. The distance from the point P to the segment BC is equal to AP \u003d 1. Find the length of the segment AD, if known that around a quadrilateral ABCD can describe a circle.
S-14. In a circle, a diameter MN and a chord AB are drawn parallel to the diameter MN. The tangent to the circle at the point M intersects the lines NA and NB, respectively, at the points P and Q. It is known that MP \u003d p, MQ \u003d q. Find MN.
S-15. A circle is drawn through the vertices A and B of triangle ABC, intersecting the sides BC and AC at points D and E, respectively. The area of \u200b\u200bthe CDE triangle is 7 times smaller than the area of \u200b\u200bthe ABDE quadrangle. Find DE and the radius of the circle if AB \u003d 4 and ∠C \u003d 45 °.
S-16. A tangent and a chord LM of length 5 are drawn through the point L of the circle. The chord MN is parallel to the tangent and equal to 6. Find the radius of the circle.
S-17. The diagonals of an inscribed ABCD quadrangle in a circle intersect at point E, with BD \u003d 6 and AD ∙ CE \u003d DC ∙ AE. Find the area of \u200b\u200bthe quadrilateral ABCD.
S-18. In triangle ABC, it is known that the length AB is 3, 
The chord KN of the circle described near the triangle ABC intersects the segments AC and BC at the points M and L, respectively. Moreover, ∠ABC \u003d ∠CML, the area of \u200b\u200bthe quadrilateral ABLM is 2, and the length of LM is 1. Find the height of the triangle KNC omitted from the vertex C and its area.
S-19. In triangle ABC, point D lies on side BC, line AD intersects the bisector of angle ACB at point O. It is known that points C, D and O lie on a circle whose center is on side AC, AC: AB \u003d 3: 2, and the DAC angle is three times larger than the DAB angle. Find the cosine of the angle ACB.
S-20. The circle inscribed in the isosceles triangle ABC touches the base AC at point D and the lateral side AB at point E. Point F is the midpoint of side AB, and point G is the intersection point of the circle and the segment FD other than D. The tangent to this circle passing through point G, crosses side AB at point H. Find the angle BCA if it is known that FH: HE \u003d 2: 3.
S-21. On segment AB, point C is taken, and on segments AB and CB, circles are constructed as on diameters. The chord AM of the larger circle touches the smaller circle at point D. The line BD intersects the large circle at point N. It is known that ноDAB \u003d a, AB \u003d 2R. Find the area of \u200b\u200bthe quadrilateral ABMN.
S-22. In triangle ABC, the bisectors AD and BL intersect at point F. The angle LFA is 60 °.
1) Find the value of the angle ACB.
2) Calculate the area of \u200b\u200btriangle ABC if ∠CLD \u003d 45 ° and AB \u003d 2.
S-23. Two circles intersect at points A and B. Through point B, a line is drawn intersecting circles at points C and D lying on opposite sides of line AB. The tangents to these circles at points C and D intersect at point E. Find AD if AB \u003d 15, AC \u003d 20, and AE \u003d 24.
S-24. In trapezoid ABCD with lateral sides AB \u003d 9 and CD \u003d 5, the bisector of angle D intersects the bisectors of angles A and C at points M and N, respectively, and the bisector of angle B intersects the same two bisectors at points L and K, and point K
lies on the basis of AD. In what respect does line LN divide side AB and line MK divide BC? Find the ratio MN: KL if LM: KN \u003d 3: 7.
Definition 10 . Arc called the part of the circle. For example, the arc AB in Figure 4. Two points on the circle define two arcs, so for accuracy we add a third point between the data, for example, speaking of the AC arc, we can mean both the larger and the smaller ones, but it’s worth saying “ADC arc” , and everything becomes clear.
Definition 11 . Central called such anglewhose vertex is the center of the circle (in Fig. 4, the angle of the AOW). This angle is also characterized by the arc on which it is operated.
Theorem 2 The angle inscribed in a circle is equal to half of the corresponding central angle.
In Fig. 4, we consider the angle of the ACB and the arc AB, on which it rests. This arc is characterized by the angle AOW, as mentioned earlier. Those. we must prove that 2∠ DIA \u003d ∠ AOW
Consider the triangle ABC in Figure 4. It is inscribed in this circle. Since the radii are equal, the triangles AOS and VOS are isosceles, therefore поэтому ACO \u003d ∠ CAO and ∠ BCO \u003d ВО CBO, therefore поэтому C \u003d ∠ ACO + ∠ BCO \u003d ∠ CAO + ∠ CBO. In the triangle ABC we write the sum of the angles: ∠ С + ∠ В + ∠ А \u003d 180 о decompose: ∠ C + ∠ CAO + ∠ NWO+ ∠ OAV + ∠ OVA \u003d 2∠ С + ∠ OAV + ∠ OVA \u003d 180 о (1).
Now we write down the sum of the angles of the triangle AOW: ∠ AOW + ∠ OAB + ∠ OVA \u003d 180 о (2), we equate equations 1 and 2: 2∠ C + ∠ OAB + ∠ OVA \u003d ∠ AOV + ∠ OAB + ∠ OVA, 2∠ C \u003d ∠ AOW, h.p. This can be proved for any angle, for example ADB. It should be noted the case when the angle is based on a diameter or an arc half the length of a circle, it will be equal to 90 ° (180 ° / 2). From here: Theorem 2.1.
If the angle inscribed in the circle is a straight line (equal to 90 degrees), then it is based on the diameter. And back
Theorem 2.2.
If the angle inscribed in the circle is based on the diameter, then it is straight (equal to 90 degrees).
It follows from Theorem 2 that the inscribed angles based on equal arcs are equal, because equal to half of the same central angle. ∠ ADB \u003d ∠ DIA \u003d 1/2 ∠ AOW
Theorem 3
Inscribed angles based on equal arcs are equal.
Theorem 4
. The value of the angle with the vertex inside the circle is equal to the half-sum of the angular values \u200b\u200bof the arcs concluded between its sides and their extensions.
Theorem 5
. The angle formed by two secants with a vertex outside the circle whose sides intersect this circle is equal to the half-difference of the angular values \u200b\u200bof the larger and smaller arcs enclosed between its sides.
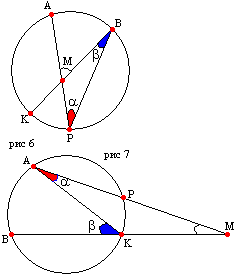
Proof of Theorem 4:
Consider the angle AMV in Fig. 6. Note that α is half the arc AB, β is half the arc KP. Knowing the theorem on the outer corner of a triangle: the outer corner of a triangle is equal to the sum of two inner ones that are not adjacent to it. Therefore, ∠ AMB \u003d α + β \u003d 1/2 (AB + KP), where AB and KP are arcs. We proved Theorem 4. Now we prove Theorem 5. For this, we consider the angle AMB in Fig. 7, formed by two secant MAs and MVs. Since α is equal to half the arc KP, β is half the arc AB, then by the property of the external angle of the triangle we get ∠ AMB \u003d β -α \u003d 1/2 (AB-KP)
Theorem 6
. At the intersection, the chords are divided into segments whose products are equal.
Draw the chords AC and BD. The inscribed angles of CAB and CDB are based on the arc of CB, therefore, ∠ CAB \u003d ∠ CDB. Similarly, ∠ ACD \u003d ∠ ABD. Thus, the triangles ASK and DBK are similar (in two angles) and KA / KD \u003d KC / KB. From here we get KA * KB \u003d KC * KD