Diskriminant - noaniq atama. Ushbu maqolada berilgan ko'payishning haqiqiy echimi bor yoki yo'qligini aniqlashga imkon beradigan ko'paytirilgan kamsituvchi haqida so'z yuritiladi. Kvadrat polinomining formulasi maktab algebra va tahlil kursida mavjud. Qanday qilib diskriminantni topish mumkin? Tenglamani yechish uchun nima kerak?
Ikkinchi darajali kvadrat polinomiya yoki tenglama deyiladi i * w ^ 2 + j * w + k 0 ga teng, bu erda "i" va "j" birinchi va ikkinchi koeffitsientdir, "k" doimiydir, uni ba'zan "bepul muddatli", "w" esa o'zgaruvchan. O'zgaruvchi o'zgaruvchanlikning barcha qiymatlari bo'ladi, bunda u identifikatorga aylanadi. 0 ga teng bo'lgan i, (w - w1) va (w - w2) hosilalari kabi tenglikni qayta yozish mumkin. Bu holda, agar “i” koeffitsienti yo'qolmasa, chap tomondagi funktsiya nolga aylanadi, faqat agar x w1 yoki w2 qiymatini qabul qilsa. Ushbu qiymatlar ko'pxaridni nolga tenglashtirish natijasidir.
Kvadrat polinomiyasi yo'qoladigan o'zgaruvchining qiymatini topish uchun biz uning koeffitsientlari asosida yordamchi qurilishdan foydalanamiz va diskriminant deb nomlaymiz. Ushbu dizayn D formulasi bo'yicha hisoblanadi j * j - 4 * i * k. U nima uchun ishlatiladi?
- Uning aytishicha, tegishli natijalar bormi.
- U ularga hisoblashda yordam beradi.
Ushbu qiymat moddiy ildizlarning mavjudligini ko'rsatadi:
- Agar u ijobiy bo'lsa, unda haqiqiy sonlar maydonida ikkita ildizni topishingiz mumkin.
- Agar diskriminant nolga teng bo'lsa, unda ikkala echim ham mos keladi. Aytishimiz mumkinki, bitta echim bor va u haqiqiy sonlar maydonidan.
- Agar diskriminant noldan kam bo'lsa, u holda ko'pxolis haqiqiy ildizlarga ega emas.
Materialni mahkamlash uchun hisob-kitob variantlari
(7 * w ^ 2; 3 * w; 1) yig'indisi uchun 0 ga teng biz D ni 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 formulasi bo'yicha hisoblaymiz -19. Noldan past bo'lgan diskriminant qiymat haqiqiy chiziqda natijalarning yo'qligini ko'rsatadi.
Agar 2 * w ^ 2 - 3 * w + 1 0 ga teng deb hisoblasak, keyin D (4; 2; 1) sonlar soniga teng bo'lgan (-3) kvadrat deb hisoblanadi va 9 - 8 ga teng, ya'ni 1. musbat qiymat haqiqiy chiziqdagi ikkita natijani ko'rsatadi.

Agar yig'indisini olsak (w ^ 2; 2 * w; 1) va 0 ga tenglashamiz, D sonlarning ko'payishini (4; 1; 1) ikkita kvadrat shaklida hisoblanadi. Ushbu ibora 4 - 4 gacha soddalashadi va yo'qoladi. Aniqlanishicha, natijalar bir xil. Agar siz ushbu formulaga diqqat bilan qarasangiz, bu "to'liq kvadrat" ekanligi ayon bo'ladi. Shu sababli, tenglikni (w + 1) ^ 2 \u003d 0 shaklida qayta yozish mumkin. Bu muammoning natijasi “-1” ekanligi ayon bo'ldi. Agar D 0 bo'lsa, tenglamaning chap tomoni har doim “kvadrat yig'indisi” formulasi bo'yicha chiqadi.
Ildizlarni hisoblashda diskriminantdan foydalanish
Ushbu yordamchi qurilish nafaqat moddiy echimlar sonini ko'rsatibgina qolmay, balki ularni topishga ham yordam beradi. Ikkinchi darajali tenglama uchun umumiy hisoblash formulasi quyidagicha:
w \u003d (-j +/- d) / (2 * i), bu erda d 1/2 darajaning diskriminantidir.
Aytaylik, diskriminant noldan past bo'lsa, unda d xayoliy va natijalari xayoliy.
D nolga teng, keyin D ga teng, 1/2 darajaga teng bo'lgan nol ham nolga teng. Yechimi: -j / (2 * i). Yana 1 * w ^ 2 + 2 * w + 1 \u003d 0 deb hisoblaymiz, -2 / (2 * 1) \u003d -1 ga teng bo'lgan natijalarni topamiz.
Aytaylik, D\u003e 0, shunday qilib d haqiqiy sondir va bu erda javob ikki qismga bo'linadi: w1 \u003d (-j + d) / (2 * i) va w2 \u003d (-j - d) / (2 * i) . Ikkala natija ham tegishli bo'ladi. 2 * w ^ 2 - 3 * w + 1 \u003d 0 ni ko'rib chiqing. Bu erda diskriminant va d birliklardir. Aniqlanishicha, w1 (3 + 1) (2 * 2) yoki 1 ga bo'linadi va w2 (3 - 1) 2 * 2 yoki 1/2 ga bo'linadi.
Kvadrat ifodani nolga tenglashtirish natijasi algoritm bo'yicha hisoblanadi:
- Amaldagi qarorlar sonini aniqlash.
- Hisoblash d \u003d D ^ (1/2).
- (-J +/- d) / (2 * i) formulaga muvofiq natijani topish.
- Tekshiruv uchun natijani asl tenglikka almashtirish.
Ba'zi maxsus holatlar
Koeffitsientlarga qarab, echim biroz soddalashtirilishi mumkin. Shubhasiz, agar o'zgaruvchining oldidagi koeffitsient nolga ikkinchi darajaga teng bo'lsa, u holda chiziqli tenglik olinadi. Agar o'zgaruvchidan oldingi koeffitsient birinchi darajadagi nolga teng bo'lsa, ikkita variant mumkin:
- ko'paytmali erkin erkin muddat bilan kvadratlar farqiga bo'linadi;
- musbat sobit bo'lgan holda real echimlar topilmaydi.
Agar bo'sh muddat nolga teng bo'lsa, unda ildizlar (0; -j) bo'ladi.
Ammo echimni topishni soddalashtiradigan boshqa maxsus holatlar mavjud.
Ikkinchi darajali kamaytirilgan tenglama
Deb nomlanadi katta kvadrat oldida koeffitsient teng bo'lgan kvadrat trinomial. Bunday vaziyatda Vetema teoremasi qo'llaniladi, unda ildizlar yig'indisi birinchi darajadagi o'zgaruvchiga koeffitsientga teng, -1 ga ko'paytiriladi va mahsulot doimiy "k" ga to'g'ri keladi.
Shuning uchun birinchi koeffitsient bitta bo'lsa, w1 + w2 -j ga teng va w1 * w2 k ga teng. Bunday tasvirning to'g'riligini tekshirish uchun birinchi formuladan w2 \u003d -j - w1 ni ifodalashimiz va uni ikkinchi tenglikka almashtirishimiz mumkin w1 * (-j - w1) \u003d k. Natijada boshlang'ich tenglik w1 ^ 2 + j * w1 + k \u003d 0 olinadi.

E'tibor qilish muhimi * w ^ 2 + j * w + k \u003d 0 ni "i" ga bo'lish orqali kamaytirish mumkin. Natijada bo'ladi: w ^ 2 + j1 * w + k1 \u003d 0, bu erda j1 - j / i va k1 - k / i.
Siz hal qilgan 2 * w ^ 2 - 3 * w + 1 \u003d 0 natijalarini w1 \u003d 1 va w2 \u003d 1/2 bilan ko'rib chiqing. Uni yarmiga bo'lish kerak, natijada w ^ 2 - 3/2 * w + 1/2 \u003d 0. Teoremaning shartlari topilgan natijalar uchun to'g'ri ekanligini tekshirib ko'ramiz: 1 + 1/2 \u003d 3/2 va 1 * 1/2 \u003d 1 / 2.
Hatto ikkinchi multiplikator
Agar birinchi darajadagi o'zgaruvchi omili (j) 2 ga bo'linsa, keyin formulani soddalashtiramiz va echimini D / 4 \u003d (j / 2) ^ 2 - i * k chorakda topamiz. u w \u003d (-j +/- d / 2) / i bo'lib, d / 2 \u003d D / 4 1/2 kuchiga teng.
Agar i \u003d 1 bo'lsa va j koeffitsienti teng bo'lsa, u holda o'zgaruvchi uchun koeffitsientning -1 va yarmi ko'payadi, shu k kvadratning doimiy ildizi minus, bu yarmining kvadratining ildizi minus bo'ladi. Formula: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.
Oliy diskriminant buyurtma
Yuqorida ko'rib chiqilgan ikkinchi darajali trinomial diskriminant - bu eng ko'p ishlatiladigan holat. Umumiy holda, ko'p a'zolardan farq qiluvchi narsa bu ko'pxaridning ildizlari farqlarining ko'paytirilgan kvadratlari. Shuning uchun nolga teng bo'lgan diskriminant kamida ikkita ko'p echimning mavjudligini ko'rsatadi.
I * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0 deb hisoblang.
D \u003d j ^ 2 * k ^ 2 - 4 * i * k ^ 3 - 4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Aytaylik, diskriminant noldan katta. Bu haqiqiy sonlar sohasida uchta ildiz borligini anglatadi. Nolda bir nechta echimlar mavjud. Agar D< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.
Video
Bizning videomuzda diskriminantni hisoblash haqida batafsil gaplashamiz.
Savolingizga javob olmadingizmi? Mualliflarga mavzuni taklif qiling.
Masalan, trinomial \\ (3x ^ 2 + 2x-7 \\) uchun diskriminant \\ (2 ^ 2-4 \\ cdot3 \\ cdot (-7) \u003d 4 + 84 \u003d 88 \\) bo'ladi. Va trinomial \\ (x ^ 2-5x + 11 \\) uchun u \\ ((- - 5) ^ 2-4 \\ cdot1 \\ cdot11 \u003d 25-44 \u003d -19 \\) ga teng bo'ladi.
Diskriminant \\ (D \\) harfi bilan belgilanadi va ko'pincha echishda ishlatiladi. Bundan tashqari, diskriminatorning qiymati bo'yicha siz grafikning qanday ko'rinishini tushunishingiz mumkin (pastga qarang).
Tenglamaning diskriminanti va ildizlari
Diskriminantning qiymati kvadrat tenglamalar sonini ko'rsatadi:
- agar ((D \\) musbat bo'lsa, tenglama ikki ildizga ega bo'ladi;
- agar \\ (D \\) nolga teng bo'lsa - bitta bitta ildiz;
- agar \\ (D \\) manfiy bo'lsa, ildiz yo'q.
Buni o'rganishingiz shart emas, shunchaki diskriminantdan (ya'ni ((\\ sqrt (D) \\)) tenglamaning ildizlarini hisoblash formulasiga kiritilganligini bilib, xulosa chiqarish juda oson: \\ (x_ (1) \u003d \\) \\ (\\ .
Agar kamsituvchi ijobiy bo'lsa
Bunday holda, uning ildizi ba'zi bir musbat sondir, ya'ni \\ (x_ (1) \\) va \\ (x_ (2) \\) qiymat jihatidan farq qiladi, chunki birinchi formulada \\ (\\ sqrt (D) \\) qo'shilgan. , ikkinchisida - chegirib tashlanadi. Va bizda ikki xil ildiz bor.
Misol
: Tenglama ildizlarini toping \\ (x ^ 2 + 2x-3 \u003d 0 \\)
Qaror
:
Javob : \\ (x_ (1) \u003d 1 \\); \\ (x_ (2) \u003d - 3 \\)
Agar diskriminant nolga teng bo'lsa
Agar diskriminant nol bo'lsa, qancha ildiz bo'ladi? Keling, asoslaylik.
Ildiz formulalari quyidagicha: \\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) va \\ (x_ (2) \u003d \\) \\ (\\ frac (-b-) \\ kvrt (D)) (2a) \\). Agar diskriminant nolga teng bo'lsa, unda uning ildizi ham nolga teng. Keyin shunday bo'ladi:
\\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + 0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)
\\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b- \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b-0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)
Ya'ni, tenglama ildizlarining qiymatlari bir-biriga mos keladi, chunki nolni qo'shish yoki olib tashlash hech narsani o'zgartirmaydi.
Misol
: Tenglama ildizlarini toping \\ (x ^ 2-4x + 4 \u003d 0 \\)
Qaror
:
|
\\ (x ^ 2-4x + 4 \u003d 0 \\) |
Biz koeffitsientlarni yozamiz: |
|
|
\\ (a \u003d 1; \\) \\ (b \u003d -4; \\) \\ (c \u003d 4; \\) |
Biz diskriminantni formula bo'yicha hisoblaymiz ((D \u003d b ^ 2-4ac \\). |
|
|
\\ (D \u003d (- 4) ^ 2-4 \\ cdot1 \\ cdot4 \u003d \\) |
Tenglamaning ildizlarini toping |
|
|
\\ (x_ (1) \u003d \\) \\ (\\ frac (- (- - 4) + \\ kvrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\) \\ (x_ (2) \u003d \\) \\ (\\ frac (- (- - 4) - \\ kvrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\) |
|
Ikkita bir xil ildizga ega edik, shuning uchun ularni alohida yozishning ma'nosi yo'q - biz bitta deb yozamiz. |
Javob : \\ (x \u003d 2 \\)
Diskriminant - noaniq atama. Ushbu maqolada berilgan ko'payishning haqiqiy echimi bor yoki yo'qligini aniqlashga imkon beradigan ko'paytirilgan kamsituvchi haqida so'z yuritiladi. Kvadrat polinomining formulasi maktab algebra va tahlil kursida mavjud. Qanday qilib diskriminantni topish mumkin? Tenglamani yechish uchun nima kerak?
Ikkinchi darajali kvadrat polinomiya yoki tenglama deyiladi i * w ^ 2 + j * w + k 0 ga teng, bu erda "i" va "j" birinchi va ikkinchi koeffitsientdir, "k" doimiydir, uni ba'zan "bepul muddatli", "w" esa o'zgaruvchan. O'zgaruvchi o'zgaruvchanlikning barcha qiymatlari bo'ladi, bunda u identifikatorga aylanadi. 0 ga teng bo'lgan i, (w - w1) va (w - w2) hosilalari kabi tenglikni qayta yozish mumkin. Bu holda, agar “i” koeffitsienti yo'qolmasa, chap tomondagi funktsiya nolga aylanadi, faqat agar x w1 yoki w2 qiymatini qabul qilsa. Ushbu qiymatlar ko'pxaridni nolga tenglashtirish natijasidir.
Kvadrat polinomiyasi yo'qoladigan o'zgaruvchining qiymatini topish uchun biz uning koeffitsientlari asosida yordamchi qurilishdan foydalanamiz va diskriminant deb nomlaymiz. Ushbu dizayn D formulasi bo'yicha hisoblanadi j * j - 4 * i * k. U nima uchun ishlatiladi?
- Uning aytishicha, tegishli natijalar bormi.
- U ularga hisoblashda yordam beradi.
Ushbu qiymat moddiy ildizlarning mavjudligini ko'rsatadi:
- Agar u ijobiy bo'lsa, unda haqiqiy sonlar maydonida ikkita ildizni topishingiz mumkin.
- Agar diskriminant nolga teng bo'lsa, unda ikkala echim ham mos keladi. Aytishimiz mumkinki, bitta echim bor va u haqiqiy sonlar maydonidan.
- Agar diskriminant noldan kam bo'lsa, u holda ko'pxolis haqiqiy ildizlarga ega emas.
Materialni mahkamlash uchun hisob-kitob variantlari
(7 * w ^ 2; 3 * w; 1) yig'indisi uchun 0 ga teng biz D ni 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 formulasi bo'yicha hisoblaymiz -19. Noldan past bo'lgan diskriminant qiymat haqiqiy chiziqda natijalarning yo'qligini ko'rsatadi.
Agar 2 * w ^ 2 - 3 * w + 1 0 ga teng deb hisoblasak, keyin D (4; 2; 1) sonlar soniga teng bo'lgan (-3) kvadrat deb hisoblanadi va 9 - 8 ga teng, ya'ni 1. musbat qiymat haqiqiy chiziqdagi ikkita natijani ko'rsatadi.

Agar yig'indisini olsak (w ^ 2; 2 * w; 1) va 0 ga tenglashamiz, D sonlarning ko'payishini (4; 1; 1) ikkita kvadrat shaklida hisoblanadi. Ushbu ibora 4 - 4 gacha soddalashadi va yo'qoladi. Aniqlanishicha, natijalar bir xil. Agar siz ushbu formulaga diqqat bilan qarasangiz, bu "to'liq kvadrat" ekanligi ayon bo'ladi. Shu sababli, tenglikni (w + 1) ^ 2 \u003d 0 shaklida qayta yozish mumkin. Bu muammoning natijasi “-1” ekanligi ayon bo'ldi. Agar D 0 bo'lsa, tenglamaning chap tomoni har doim “kvadrat yig'indisi” formulasi bo'yicha chiqadi.
Ildizlarni hisoblashda diskriminantdan foydalanish
Ushbu yordamchi qurilish nafaqat moddiy echimlar sonini ko'rsatibgina qolmay, balki ularni topishga ham yordam beradi. Ikkinchi darajali tenglama uchun umumiy hisoblash formulasi quyidagicha:
w \u003d (-j +/- d) / (2 * i), bu erda d 1/2 darajaning diskriminantidir.
Aytaylik, diskriminant noldan past bo'lsa, unda d xayoliy va natijalari xayoliy.
D nolga teng, keyin D ga teng, 1/2 darajaga teng bo'lgan nol ham nolga teng. Yechimi: -j / (2 * i). Yana 1 * w ^ 2 + 2 * w + 1 \u003d 0 deb hisoblaymiz, -2 / (2 * 1) \u003d -1 ga teng bo'lgan natijalarni topamiz.
Aytaylik, D\u003e 0, shunday qilib d haqiqiy sondir va bu erda javob ikki qismga bo'linadi: w1 \u003d (-j + d) / (2 * i) va w2 \u003d (-j - d) / (2 * i) . Ikkala natija ham tegishli bo'ladi. 2 * w ^ 2 - 3 * w + 1 \u003d 0 ni ko'rib chiqing. Bu erda diskriminant va d birliklardir. Aniqlanishicha, w1 (3 + 1) (2 * 2) yoki 1 ga bo'linadi va w2 (3 - 1) 2 * 2 yoki 1/2 ga bo'linadi.
Kvadrat ifodani nolga tenglashtirish natijasi algoritm bo'yicha hisoblanadi:
- Amaldagi qarorlar sonini aniqlash.
- Hisoblash d \u003d D ^ (1/2).
- (-J +/- d) / (2 * i) formulaga muvofiq natijani topish.
- Tekshiruv uchun natijani asl tenglikka almashtirish.
Ba'zi maxsus holatlar
Koeffitsientlarga qarab, echim biroz soddalashtirilishi mumkin. Shubhasiz, agar o'zgaruvchining oldidagi koeffitsient nolga ikkinchi darajaga teng bo'lsa, u holda chiziqli tenglik olinadi. Agar o'zgaruvchidan oldingi koeffitsient birinchi darajadagi nolga teng bo'lsa, ikkita variant mumkin:
- ko'paytmali erkin erkin muddat bilan kvadratlar farqiga bo'linadi;
- musbat sobit bo'lgan holda real echimlar topilmaydi.
Agar bo'sh muddat nolga teng bo'lsa, unda ildizlar (0; -j) bo'ladi.
Ammo echimni topishni soddalashtiradigan boshqa maxsus holatlar mavjud.
Ikkinchi darajali kamaytirilgan tenglama
Deb nomlanadi katta kvadrat oldida koeffitsient teng bo'lgan kvadrat trinomial. Bunday vaziyatda Vetema teoremasi qo'llaniladi, unda ildizlar yig'indisi birinchi darajadagi o'zgaruvchiga koeffitsientga teng, -1 ga ko'paytiriladi va mahsulot doimiy "k" ga to'g'ri keladi.
Shuning uchun birinchi koeffitsient bitta bo'lsa, w1 + w2 -j ga teng va w1 * w2 k ga teng. Bunday tasvirning to'g'riligini tekshirish uchun birinchi formuladan w2 \u003d -j - w1 ni ifodalashimiz va uni ikkinchi tenglikka almashtirishimiz mumkin w1 * (-j - w1) \u003d k. Natijada boshlang'ich tenglik w1 ^ 2 + j * w1 + k \u003d 0 olinadi.

E'tibor qilish muhimi * w ^ 2 + j * w + k \u003d 0 ni "i" ga bo'lish orqali kamaytirish mumkin. Natijada bo'ladi: w ^ 2 + j1 * w + k1 \u003d 0, bu erda j1 - j / i va k1 - k / i.
Siz hal qilgan 2 * w ^ 2 - 3 * w + 1 \u003d 0 natijalarini w1 \u003d 1 va w2 \u003d 1/2 bilan ko'rib chiqing. Uni yarmiga bo'lish kerak, natijada w ^ 2 - 3/2 * w + 1/2 \u003d 0. Teoremaning shartlari topilgan natijalar uchun to'g'ri ekanligini tekshirib ko'ramiz: 1 + 1/2 \u003d 3/2 va 1 * 1/2 \u003d 1 / 2.
Hatto ikkinchi multiplikator
Agar birinchi darajadagi o'zgaruvchi omili (j) 2 ga bo'linsa, keyin formulani soddalashtiramiz va echimini D / 4 \u003d (j / 2) ^ 2 - i * k chorakda topamiz. u w \u003d (-j +/- d / 2) / i bo'lib, d / 2 \u003d D / 4 1/2 kuchiga teng.
Agar i \u003d 1 bo'lsa va j koeffitsienti teng bo'lsa, u holda o'zgaruvchi uchun koeffitsientning -1 va yarmi ko'payadi, shu k kvadratning doimiy ildizi minus, bu yarmining kvadratining ildizi minus bo'ladi. Formula: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.
Oliy diskriminant buyurtma
Yuqorida ko'rib chiqilgan ikkinchi darajali trinomial diskriminant - bu eng ko'p ishlatiladigan holat. Umumiy holda, ko'p a'zolardan farq qiluvchi narsa bu ko'pxaridning ildizlari farqlarining ko'paytirilgan kvadratlari. Shuning uchun nolga teng bo'lgan diskriminant kamida ikkita ko'p echimning mavjudligini ko'rsatadi.
I * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0 deb hisoblang.
D \u003d j ^ 2 * k ^ 2 - 4 * i * k ^ 3 - 4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Aytaylik, diskriminant noldan katta. Bu haqiqiy sonlar sohasida uchta ildiz borligini anglatadi. Nolda bir nechta echimlar mavjud. Agar D< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.
Video
Bizning videomuzda diskriminantni hisoblash haqida batafsil gaplashamiz.
Savolingizga javob olmadingizmi? Mualliflarga mavzuni taklif qiling.
Muhim! Funktsiya hatto ko'paytmaning ildizida belgini o'zgartirmaydi.
E'tibor bering! Maktab algebrasi kursidagi har qanday chiziqli bo'lmagan tengsizliklar interval usuli yordamida hal qilinishi kerak.
Men sizga batafsil ma'lumotni taklif qilaman tengsizliklarni interval usuli bilan echish algoritmibundan keyin qachon xato qilmaslik mumkin nochiziqli tengsizliklarni hal qilish.
Kvadrat tenglamalarni salbiy diskriminantlar bilan echish
Biz bilganimizdek
i 2 = - 1.
Ammo,
(- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1.
Shunday qilib, kvadrat ildizning kamida ikkita qiymati bor - 1, ya'ni i va - i . Ammo, ehtimol, kvadratlari teng bo'lgan boshqa murakkab sonlar ham bor - 1?
Bu savolga aniqlik kiritish uchun, kompleks sonning kvadratini deylik a + bi teng - 1. Keyin
(a + bi ) 2 = - 1,
lekin 2 + 2abi - b 2 = - 1
Ikki murakkab sonlar, agar ularning haqiqiy qismlari va xayoliy qismlarning koeffitsientlari teng bo'lsa, ular tengdir. Shuning uchun
| { | va 2 - b 2 = - 1 ab = 0 (1) |
Tizimning ikkinchi tenglamasiga ko'ra (1), kamida bitta raqam lekin va b nolga teng bo'lishi kerak. Agar b \u003d 0, keyin birinchi tenglama hosil bo'ladi lekin 2 \u003d - 1. Raqam lekin tegishli va shuning uchun lekin 2 > 0. Salbiy bo'lmagan son lekin 2 manfiy sonni tenglashtira olmaydi - 1. Demak, tenglik b Bu holda \u003d 0 mumkin emas. Shuni tan olish kerak lekin \u003d 0, lekin keyin tizimning birinchi tenglamasidan biz olamiz: - b 2 = - 1, b \u003d ± 1.
Shuning uchun kvadratlari -1 bo'lgan murakkab sonlar faqat sonlardir i va - i , Shartli ravishda quyidagicha yoziladi:
√-1 \u003d ± i .
Shunga o'xshash sabablarga ko'ra, talabalar kvadrat soni manfiy songa teng ikkita ikkita son borligiga ishonch hosil qilishlari mumkin - lekin . Bu raqamlar √ ai va -√ ai . Shartli ravishda, u quyidagicha yozilgan:
√- a = ± √ ai .
Under ostida a Bu erda biz arifmetikani, ya'ni ijobiy, ildizni nazarda tutamiz. Masalan, √4 \u003d 2, √9 \u003d .3; shuning uchun
√-4 = + 2i , √-9 \u003d ± 3 i
Agar ilgari kvadrat tenglamalarni salbiy diskriminantlar bilan ko'rib chiqayotganda, biz bunday tenglamalarning ildizlari yo'qligini aytgan edik, endi bunday deyish endi mumkin emas. Salbiy kamsituvchi kvadratik tenglamalar murakkab ildizlarga ega. Ushbu ildizlar ma'lum formulalar bo'yicha olinadi. Masalan, tenglama berilsin x 2 + 2x + 5 \u003d 0; keyin
x 1,2 \u003d - 1 ± √1 -5 \u003d - 1 ± √-4 \u003d - 1 ± 2 i .
Demak, bu tenglama ikkita ildizga ega: x 1 = - 1 +2i , x 2 = - 1 - 2i . Bu ildizlar o'zaro birlashadi. Shunisi qiziqki, ularning yig'indisi - 2, mahsulot esa 5 ga teng, shunda Vetnam teoremasi ushlab turadi.
Kompleks son haqida tushuncha
Kompleks son bu a + ib shaklining ifodasidir, bu erda a va b har qanday haqiqiy sonlar, i - xayoliy birlik deb ataladigan maxsus raqam. Bunday iboralar uchun tenglik tushunchasi va qo'shish va ayirish amallari quyidagicha kiritiladi:
- Ikkita murakkab sonlar a + ib va \u200b\u200bc + id teng va agar bo'lsa, deyiladi
a \u003d b va c \u003d d. - A + ib va \u200b\u200bc + id ikkita kompleks sonlarning yig'indisi kompleks son deb ataladi
a + c + i (b + d). - A + ib va \u200b\u200bc + id ikkita murakkab sonlarning mahsuloti bu murakkab son
ac - bd + i (reklama + bc).
Murakkab raqamlar ko'pincha bitta harf bilan belgilanadi, masalan, z \u003d a + ib. A haqiqiy son z kompleks sonning haqiqiy qismi deyiladi, haqiqiy qism a \u003d Re z bilan belgilanadi. Haqiqiy b raqamiga z kompleks sonning xayoliy qismi deyiladi, xayoliy qism b \u003d Im z bilan belgilanadi. Bunday nomlar murakkab sonlarning quyidagi maxsus xususiyatlari tufayli tanlanadi.
Biz z \u003d a + i · 0 shakldagi murakkab raqamlar bo'yicha arifmetik amallar haqiqiy sonlar bilan bir xil tarzda bajarilganligini ta'kidlaymiz. Darhaqiqat
Shunday qilib, a + i · 0 shaklidagi murakkab raqamlar tabiiy sonlar bilan aniqlanadi. Shu sababli, ushbu turdagi murakkab raqamlar shunchaki haqiqiy deb nomlanadi. Shunday qilib, haqiqiy sonlar to'plami murakkab sonlar to'plamida mavjud. Ko'plab murakkab raqamlar ko'rsatilgan. Biz buni aniqladik, aniqrog'i
Haqiqiy raqamlardan farqli o'laroq, 0 + ib shaklidagi raqamlar xayoliy deb ataladi. Ko'pincha ular oddiygina bi yozadilar, masalan, 0 + i 3 \u003d 3 i. Sof xayoliy raqam i1 \u003d 1 i \u003d i ajoyib xususiyatga ega:
Shunday qilib,
№ 4 .1. Matematikada raqamli funktsiya - bu aniqlanish va qiymatlar sohalari raqamli to'plamlarning kichik to'plamlari bo'lgan funktsiya bo'lib, odatda haqiqiy sonlar to'plami yoki murakkab sonlar to'plami.
Funktsiya grafigi
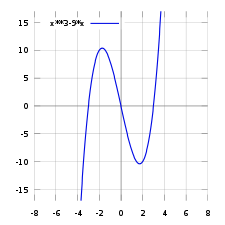
Funktsiya grafigining parchasi
Funktsiya yo'llari
tahrirlash Tahlil usuli
Odatda, funktsiya o'zgaruvchilar, operatsiyalar va elementar funktsiyalarni o'z ichiga olgan formuladan foydalanib aniqlanadi. Ehtimol, aniq ish, ya'ni turli xil qiymatlar uchun farq qiladi.
tahrirlash Jadval usuli
Funktsiya barcha mumkin bo'lgan dalillar va ular uchun qiymatlarni ro'yxatlash orqali aniqlanishi mumkin. Shundan so'ng, agar kerak bo'lsa, funktsiyani jadvalda bo'lmagan dalillar uchun interpolatsiya yoki ekstrapolyatsiya yo'li bilan aniqlash mumkin. Misollar dastur qo'llanmasini, poezdlar jadvalini yoki Boolean funktsiyasi uchun qiymatlar jadvalini o'z ichiga oladi:
tahrirlash Grafik usul
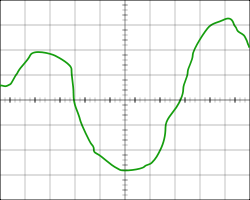
To'lqin shakli ba'zi bir funktsiyaning qiymatini grafik ravishda o'rnatadi.
Funktsiyani grafikaning ko'p nuqtalarini tekislikda ko'rsatish orqali grafik ravishda o'rnatish mumkin. Bu funktsiyaning ko'rinishi yoki qurilmadan olingan ma'lumotlar, masalan, osiloskopning taxminiy eskizi bo'lishi mumkin. Topshiriq berishning ushbu usuli aniqlik etishmasligidan aziyat chekishi mumkin, ammo ba'zi hollarda boshqa tayinlash usullari umuman qo'llanilmaydi. Bundan tashqari, funktsiyalarni idrok etish va yuqori sifatli evristik tahlil qilish uchun qulay, taqdim etiladigan usullardan biri.
tahrirlash Rekursiv usul
Funktsiya rekursiv ravishda, ya'ni o'zi orqali belgilanishi mumkin. Bunday holda, funktsiyaning ba'zi qiymatlari uning boshqa qiymatlari orqali aniqlanadi.
- faktorial;
- fibonachchi raqamlari;
- ackerman funktsiyasi.
tahrirlash Og'zaki usul
Funktsiyani tabiiy tilda so'zlar bilan har qanday aniq ma'noda ifodalash mumkin, masalan, kirish va chiqish qiymatlarini tavsiflash yoki funktsiya ushbu qiymatlar orasidagi muvofiqlikni o'rnatadigan algoritm. Grafik usul bilan bir qatorda, ba'zida bu funktsiyani tavsiflashning yagona yo'li, garchi tabiiy tillar rasmiy tillar kabi deterministik bo'lmasa ham.
- pi yozuvidagi raqamni uning raqamiga qarab qaytaradigan funktsiya;
- koinotdagi atomlar sonini ma'lum bir vaqtda qaytaradigan funktsiya;
- odamni tortishuv sifatida qabul qiladigan va uning tug'ilishidan keyin tug'iladigan odamlarning sonini qaytaradigan funktsiya


