This topic has wide practical application, so we will consider some types of problem solving. Recall that any construction is carried out exclusively with the help of a compass and a ruler.

Example 1:

Draw a triangle on two sides and a corner between them.

Given: Suppose the analyzed triangle looks like this

Fig. 1.1. The analyzed triangle for example 1

Let the given segments be c and a, and the given angle will be

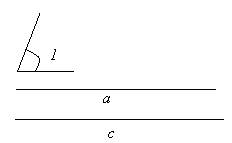
Fig. 1.2. Defined items for example 1

Build:

Angle 1 should be set aside first.

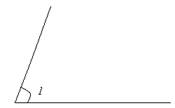
Fig. 1.3. Deferred angle 1 for example 1

Then on the sides of a given angle we lay aside these two sides with a compass: measure the length of the side with a compass a   and place the point of the compass at the top of the corner 1, and with the other part we make a notch on the side of the corner 1. We perform a similar procedure with from

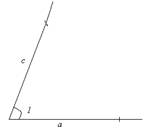
Fig. 1.4. Deferred parties a   and from   for example 1

Then we connect the received notches, and we get the desired triangle ABC

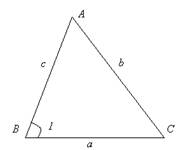
Fig. 1.5. The constructed triangle ABC for example 1

Will this triangle be equal to the intended one? It will, because the elements of the resulting triangle (two sides and the angle between them) are respectively equal to the two sides and the angle between them, given in the condition. Therefore, by the first property of the equality of triangles - is the desired one.

The construction is completed.

Note:

Recall how to set aside an angle equal to this.

Example 2

Set aside a given angle from a given ray. The angle A and the OM beam are given. Build.

Build:

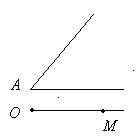
Fig. 2.1. Condition for example 2

1. Build a circle Okr (A, r \u003d AB). Points B and C are the intersection points with the sides of angle A

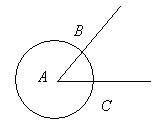
Fig. 2.2. Solution for example 2

1. Draw a circle Ocr (D, r \u003d CB). Points E and M - are the points of intersection with the sides of angle A

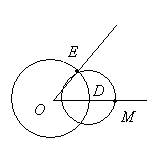
Fig. 2.3. Solution for example 2

1. MY angle is the desired angle, as .

The construction is completed.

Example 3

Construct a triangle ABC on the known side and two adjacent corners.

Let the analyzed triangle look like this:

Fig. 3.1. Condition for example 3

Then the given segments look like this

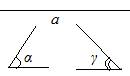
Fig. 3.2. Condition for example 3

Build:

Put the angle on the plane

Fig. 3.3. Solution for example 3

Put on the side of the given angle the length of the side a

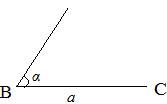
Fig. 3.4. Solution for example 3

Then set aside the angle from the vertex C. The non-common sides of the angles γ and α intersect at point A

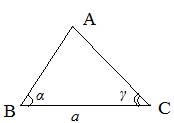
Fig. 3.5. Solution for example 3

Is the constructed triangle the desired one? It is, since the side and two adjacent corners of the constructed triangle, respectively, are equal to the side and the angle between them, given in the condition

Searched for the second sign of equality of triangles

Construction completed

Example 4

Build a triangle in 2 legs

Let the analyzed triangle look like this

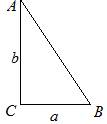
Fig. 4.1. Condition for example 4

Known elements - legs

Fig. 4.2. Condition for example 4

This task differs from the previous ones in that the angle between the sides can be determined by default - 90 0

Build:

Put the angle equal to 90 0. We will do this exactly as shown in example 2

Fig. 4.3. Solution for example 4

Then on the sides of the given angle we postpone the lengths of the sides a   and bdata provided

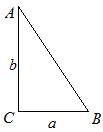
Fig. 4.4. Solution for example 4

As a result, the resulting triangle is the desired one, because its two sides and the angle between them are respectively equal to two sides and the angle between them, given in the condition

Note that the angle 90 0 can be delayed by constructing two perpendicular straight lines. How to perform this task, consider in an additional example

Additional example

Restore the perpendicular to the straight line p passing through point A,

Line p, and point A lying on this line

Fig. 5.1. Condition for an additional example

Build:

First, we construct a circle of arbitrary radius centered at point A

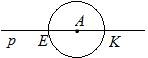
Fig. 5.2. Solution to an additional example

This circle intersects the line rat points K and E. Then we construct two circles Okr (K, R \u003d KE), Okr (E, R \u003d KE). These circles intersect at points C and B. The segment CB is the desired one,

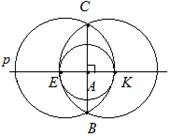
Fig. 5.3. Answer to an additional example

1. A single collection of digital educational resources ().
2. Math tutor ().

1. No. 285, 288. Atanasyan L. S., Butuzov V. F., Kadomtsev S. B., Poznyak E. G., Yudina I. I. edited by A. Tikhonov. Geometry. Grades 7–9. M .: Education. 2010 year
2. Create an isosceles triangle on the side and corner, opposite the base.
3. Construct a right triangle by hypotenuse and acute angle
4. Draw a triangle by the angle, height and bisector drawn from the top of the given angle.

§1. Building a triangle on two sides and the angle between them

The construction of a geometric figure is one of the interesting problems in geometry. It is not easy to get the necessary figure only with the help of a compass and ruler without divisions.

The triangle shape is often used in solving problems, but how to build it correctly?

Let it be necessarybuild a triangle on two sides and a corner between them.

First, what are two sides - these are two arbitrary segments, for example,P 1 Q 1 and P 2 Q 2 , as well as an arbitrary angle alpha. All these elements are already built, in other words, these elements are given the task.

Secondly, it is necessary to determine the sequence of construction: first you need to build one side of the triangle, then the corner and then the second side of the triangle.

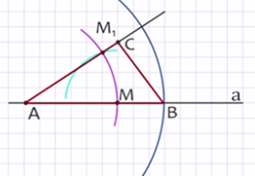So, before us is a white sheet, draw a line a and mark point A on it, then take a compass and set aside the segment AB equal to the segmentP 1 Q 1 . Next, we choose an arbitrary solution of the compass and draw one circle centered at the vertex of the angle alpha and the other centered at point A. The first circle will intersect the rays of the angle alpha at points P and K, and the second circle will intersect the line a at point M. Draw a segment RK. Then we take a compass solution equal to a segment of the RC, and construct a circle with a center at point M. A circle with a center at point M will intersect a circle with a center at point A, let this point be M 1. Draw beam AM 1. Then on the beam AM 1 we set aside the segment AC equal to the segment P 2Q 2 . Connect the points B and C by a segment. The resulting triangle ABC is the desired one.

Now we prove that the obtained triangle ABC is the desired one. In fact, the segment AB is equal to the segmentP 1 Q 1   and the segment AC is equal to the segmentP 2 Q 2   by construction. The angle alpha is also equal in construction to the angle of the CAB. With this construction progress for any given segmentsP 1 Q 1 and P 2 Q 2   and the untapped angle alpha, the desired triangle can be constructed. Since the line a and the point A on it can be chosen arbitrarily, there are infinitely many triangles satisfying the conditions of the problem. All these triangles are equal to each other according to the first sign of equality of triangles, therefore it is customary to say that this problem has a unique solution.

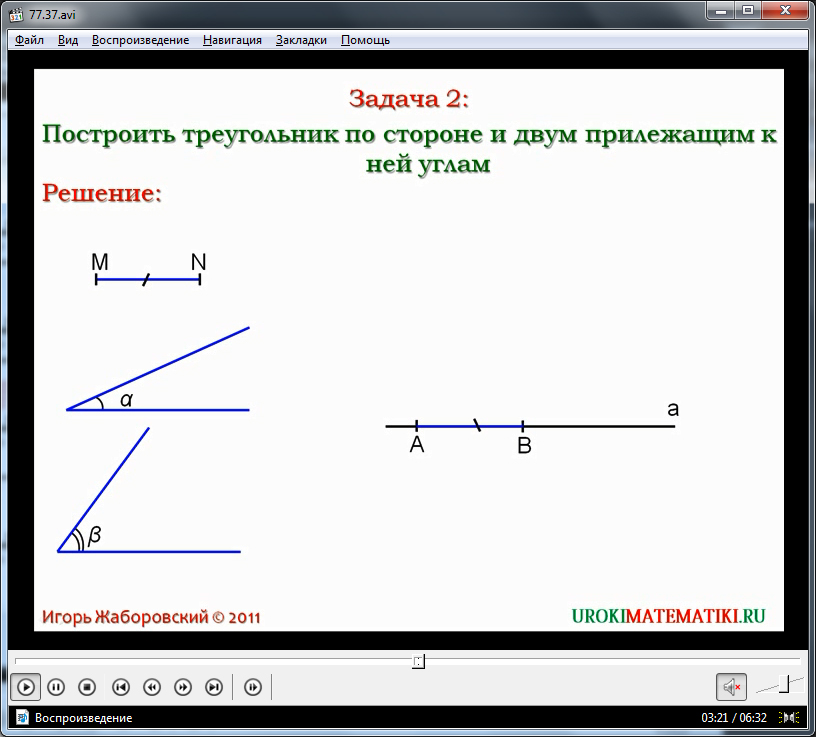
  §2. Building a triangle on the side and two adjacent corners

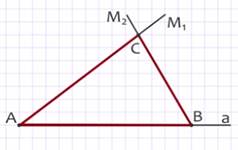Now consider the problembuilding a triangle along the side and two adjacent corners.

So, we are given a segmentPq   and two angles alpha and beta. Draw a line a and mark on it an arbitrary point A. Let us set aside the segment AB from the point A equal to the segmentPq . Then we construct an angle M 1 AB with a vertex at point A equal to the angle alpha, and an angle M 2 VA with a vertex at point B equal to the angle beta. The intersection point of the rays AM 1 and VM 2 will be point C. The triangle ABC is the desired one.

Let us prove this: the segment AB is equal to the segmentPq by construction, also by construction, the angle of the CAB is equal to the angle alpha, and the angle of CBA is equal to the angle beta.

As you know, the sum of the angles in a triangle is 180 degrees, so with this construction process, the desired ABC triangle can only be built if the sum of the angles of alpha and beta is less than 180 degrees. If the sum of these angles is greater than or equal to 180 degrees, it is impossible to build a triangle.

In this problem, as in the previous one, the line a and point A on it can be chosen arbitrarily, which means that there are infinitely many triangles satisfying the conditions of the problem. All these triangles are equal to each other in the second sign of equality of triangles, therefore they say that this problem has a unique solution.

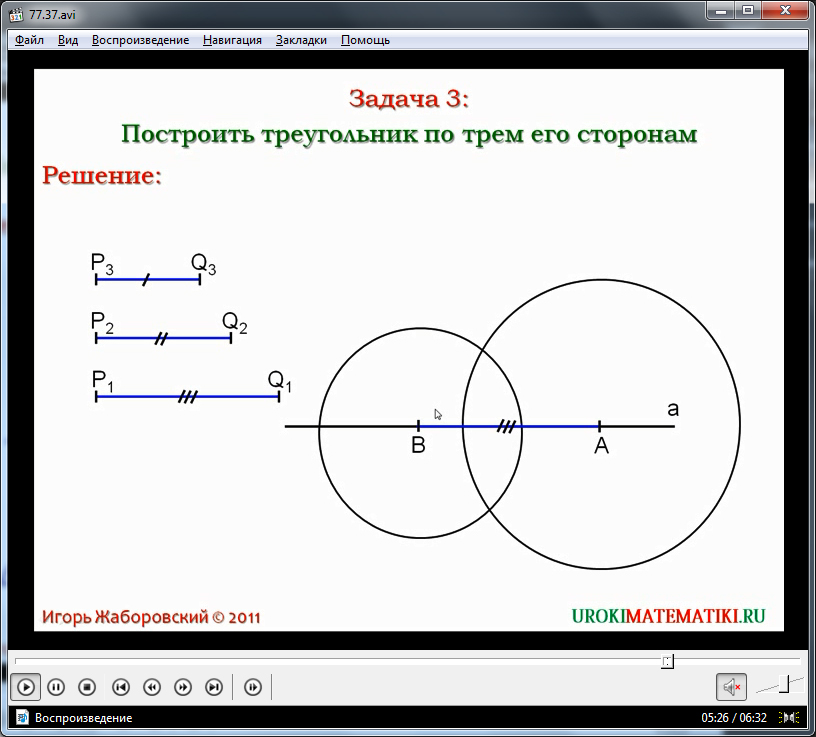
  §3. Building a triangle on three sides

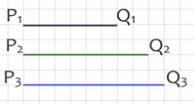Draw a triangle on three sidesis the third task of constructing a triangle.

Let us be given three segmentsP 1 Q 1, P 2 Q 2 and P 3 Q 3 . it is necessary to construct a triangle ABC, in which AB is equal toP 1 Q 1, BC equals P 2 Q 2 and CA equals P 3 Q 3.

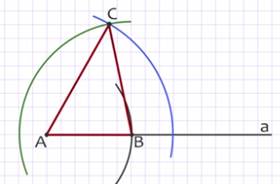Draw a line a and on it with the help of a compass we set aside the segment AB equal to the segmentP 1 Q 1 . Then we construct two circles: one with the center at point A and radiusP 3 Q 3 and the other with center at point B and radiusP 2 Q 2 . Let point C be one of the intersection points of these circles. Having drawn the segments AC and BC, we obtain the desired triangle ABC. In fact, by the construction of AB equalsP 1 Q 1, BC is P 2 Q 2 and CA is P 3 Q 3 , that is, the sides of the triangle are equal to these segments.

The considered problem does not always have a solution due to the action of the triangle inequality, that is, in any triangle the sum of any two sides is greater than the third side, therefore, if any of these segments is greater than or equal to the sum   two others, it is impossible to construct a triangle whose sides would be equal to given segments.

Literature:

1. Atanasyan L.S. Textbook: Geometry. Grades 7-9: textbook. for general education. organizations / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al. - M.: Education, 2013. –383 p.

2. Geometry. Part I. Planimetry: tutorial/ I.B. Barsky, G.N. Timofeev. - Yoshkar-Ola: publishing house of the Mari state. University, 2006 and 2008. - 636s

The video tutorial “Building a triangle in three elements” contains examples of solving three problems in constructing a triangle in three given elements. This topic has an important practical value. Formed ability to make correct construction of triangles is an important basis for further development of skills. geometric constructionssolving problems. Therefore, the task of this video tutorial is to form an idea of \u200b\u200bthe correct solution of practical problems in constructing a triangle using three elements. The video material may accompany the teacher’s explanation on the topic, serving to provide examples that are simultaneously fixed by the corresponding similar constructions in the notebook. Also, the material can be used instead of explaining the teacher as an independent part of the lesson.

To solve the problems of the lesson, the teacher is helped by the tools of the video material, which facilitate understanding and remembering it. High visibility of the explanation is achieved with the help of animation effects, the possibility of highlighting concepts and construction details with color. “Live” presentation of the material allows you to keep the attention of students on the subject being studied, deepens understanding of the processes when solving geometric tasks.

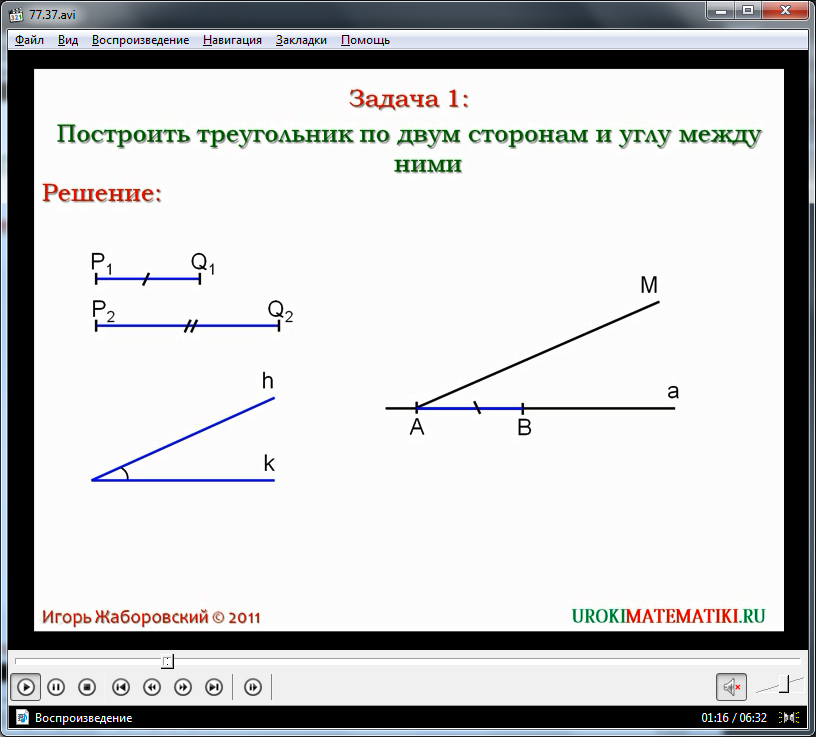
After presenting the topic of the video tutorial, the demonstration begins with the statement of the terms of the first task. It is proposed to construct a triangle on the given two sides of it and the angle formed by them. Forming skills for solving geometric problems, the need to parse the problem into a condition and a question is recalled. To be clarified, in this problem the values \u200b\u200bof some two sides of the triangle and the angle that they form are given. The screen shows the segments that make up the sides of the triangle - for the first side P 1 Q 1 and the segment for constructing the second side P 2 Q 2, as well as the angle ∠hk. It is proposed to solve this construction problem with the help of a compass and an ordinary ruler without divisions. As a result of construction, a triangle ΔABC should be obtained in which AB \u003d P 1 Q 1, AC \u003d P 2 Q 2, and the angle углаA between them is equal to the given angle углуhk. The construction begins with laying on the line a of the segment AB \u003d P 1 Q 1, using the compass. Then, from the point A, a ray AM is constructed, which forms an angle equal to ∠hk with a straight line a. Further on this ray the segment AC \u003d P 2 Q 2 is postponed. The ends of the obtained segments AB and AC are connected by the segment BC. Thus, the desired triangle with given sides and angle is constructed. It is noted that all the given conditions are satisfied by construction. Such a task is feasible. Since when building it is possible to choose an arbitrary straight line and a point to start building, there will be infinitely many such triangles. All such triangles will be equal to each other at the first sign of equality. It is reported that in this regard it is believed that this task has a unique solution.

Further, during the video tutorial, it is proposed to solve the second problem of construction. It is necessary to build a triangle with the given side and two adjacent corners. The conditions of this task are shown on the screen — the available segment MN, the angles ∠α and ∠β. It is necessary to construct a triangle ΔABC, whose side AB is equal to the existing segment, and the adjacent angles ∠A and ∠B are equal to the values \u200b\u200bof the available angles ∠α and ∠β. The construction begins with the compass laying on the line a of the side AB equal to the segment MN. From point A, an angle is laid that is equal to the existing angle ∠α. An angle equal to ∠β is plotted from point B. The intersection point of the constructed rays thus constructed, which are part of the measured angles, is the third vertex ΔABC. The constructed triangle is the desired geometric figure. The figure shows the correspondence of the problem conditions to the construction made.

In the last part of the video tutorial, it is proposed to build a triangle on given three sides. To construct a triangle, three segments are displayed on the screen - the first P 1 Q 1, the second P 2 Q 2 and the third P 3 Q 3. It is necessary to construct a triangle ΔABC in which the sides will be equal to the lengths of the given segments: AB \u003d P 1 Q 1, CA \u003d P 2 Q 2, side BC \u003d P 3 Q 3. The construction begins by laying off the segment AB on some straight line a. Its length is laid equal to the length P 1 Q 1. To build the following sides, circles are drawn at points A and B. The radius of the first circle is equal to the length P 2 Q 2, the length P 3 Q 3 determines the radius of the second circle. After constructing the circles, two points of their intersection are obtained. Mark one of the points as C, the last remaining unfinished vertex of the triangle ΔABC. Combining the constructed vertex C with the strings A and B, we obtained a solution to the problem. It is noted that all sides of the triangle correspond to the condition of the problem and are equal, respectively, to the initially specified segments. At the same time, a peculiarity of this problem is noted - it may not always have a solution. Students are reminded that from the theorem studied earlier, it is known that any side of a triangle is always less than the sum of its two other sides. Therefore, for cases when the length of one given segment is equal to the sum of the remaining two or more, the problem has no solution - the triangle inequality condition is not fulfilled.

The video lesson “Building a triangle in three elements” can be used by a teacher in a geometry lesson in school. Also, the material will help to form the skills of solving the problems under consideration for the construction of an independent study of the material, can be recommended for distance learning.