Рис. 33 Образец выполнения задания по разложению числа 7 тремя разными способами

Для самостоятельного разложения числа 6 и 8.

В качестве дидактического материала применяются «пустые» карточки и наборы предметов, которые ребенок может использовать для выполнения задания. Образец разложения предметов на карточке смотрите на рисунке 33.

Упражнение 3. «Перечисли все способы разложения числа 5 (4, 3) на два наименьших числа».

Упражнение выполняется в устной форме.

Упражнение 4. «Заполни таблицу».

Рис. 34 Карточки-таблицы предлагаемые детям для выполнения задания

Для работы детям предлагаются карточки-таблицы, образцы которых приведены выше, и наборы цифр в таком объеме, чтобы их хватило для заполнения всех вариантов карточек.

Результаты 2-4 упражнения оцениваются следующим образом. Если ребенок выполняет разложение чисел на два наименьших числа в пределах первого десятка без ошибок, педагог фиксирует высокий уровень усвоения учебного материала. Если ребенок знаком со всеми способами разложения не менее 6 чисел первого десятка, педагог фиксирует средний уровень усвоения учебного материала. В том случае, если дети усвоили способы разложений менее 6 натуральных чисел первого десятка, уровень усвоения учебного материала считается низким.

Тесты на определение уровня овладения

Детьми вычислительной деятельностью

Тесты на выявление уровня сформированности представлений об арифметических действиях «сложение» и «вычитание»

Для детей 5-7 лет

В данный раздел включены четыре теста, позволяющие выявить уровень представлений детей об арифметических действиях «сложение» и «вычитание». Первый тест представлен целостным комплексом заданий, каждое из которых направлено на выявление определенных знаний детей по исследуемой теме. По результатам выполнения этих заданий педагог может судить о том, насколько ребенок осознал смысл арифметического действия. Тесты 2 - 4 позволяют определить, насколько ребенок усвоил отношения между числами и знаками в арифметическом действии.

Тест 1. Тест включает четыре задания с одним и тем же дидактическим материалом. В качестве дидактического материала предлагаются карточки с арифметическими действиями на сложение и вычитание.

Упражнение используется при тестировании как детей старшей, так и подготовительной группы. При этом изменения вносятся только в дидактический материал, а именно: подбираются карточки с арифметическими выражениями по составу наиболее сложными, чем в предыдущих заданиях. Это становится возможным и необходимым в связи с тем, что каждый следующий этап обучения предполагает постепенное увеличение отрезка натурального ряда чисел, внутри которого дети выполняют арифметические действия, и осваивают закономерности образования нового числа.

7 – 1 = 6

5 – 2 = 3

3 + 2 = 5

6 + 1 = 7

6 – 3 = 3

2 + 2 = 4

Рис. 35 Карточки с арифметическими выражениями

В данном случае ребенок должен просто продемонстрировать умение читать арифметическое выражение.

Задание 2. Ребенка просят объяснить, что обозначают эти арифметические выражения.

При выполнении этой части задания дошкольник должен показать, что не только умеет читать арифметические выражения, но и понимает смысл каждого из них. К правильным ответам относятся примерно следующие: «если к трем каким-либо предметам, добавить еще два каких-либо предметов, то получится 5 предметов». Вместе с тем, учитывая возможное отсутствие необходимых навыков выражения своих мыслей, можно предложить следующие задания (третье и четвертое), которые помогут вам определить, насколько ребенок понимает смысл арифметических действий.

Задание 3. Педагог выбирает из предложенных арифметических выражений два: одно на сложение и одно на вычитание и предлагает ребенку при помощи игрушек (предлагается несколько наборов мелких игрушек, например, матрешки и зайчики) продемонстрировать эти действия. Игрушки следует использовать двух видов, а количество каждого вида игрушек не менее 10 штук.

Примеры вариантов правильного выполнения задания по выражению 3+2=5 приведены ниже.

«Если мы возьмем 3 матрешки и к ним добавим 2 зайчика, то получим 5 игрушек».

«Если мы возьмем 3 зайчика и добавим к ним 2 матрешки, то получим 5 игрушек».

«Если мы возьмем 3 зайчика и добавим к ним еще 2 зайчика, то получим 5 зайчиков».

«Если мы возьмем 2 матрешки и добавим к ним еще 3 матрешки, то получим 5 матрешек».

Таким образом, при использовании двух совокупностей разнородных предметов можно составить четыре варианта ответа на данный вопрос. При тестировании педагогу следует побуждать ребенка к нахождению различных вариантов ответа, задавая им вопрос: а как еще можно составить это арифметическое действие с предложенными игрушками?

Задание 4. Педагог выбирает еще два варианта карточек из предложенных (одну на сложение, другую на вычитание) и предлагает составить по ним арифметические задачи.

При работе с детьми подготовительной к школе группы используются еще и тесты приведенные ниже. Они проводятся как в начале учебного года, так и в конце. Изменения вносятся лишь в используемый при тестировании дидактический материал (на конец учебного года берутся большие числа). При этом все задания к тестам остаются прежними.

Тест 2. «Составь арифметическое действие». Педагог просит детей из чисел 5, 2 и 3 составить арифметическое действие на вычитание. Задает вопрос: «Сколько таких действий можно составить»?

Тест 3. «Составь обратное арифметическое выражение»

Пример: 10 – 5 = 5 5 + 5 = 10

Для самостоятельной работы: 5 – 3 = 2

Тест 4. « Подбери к схеме арифметическое действие».

Детям поочередно предъявляются различные схемы к арифметическим задачам на сложение и вычитание (рисунок смотрите ниже).

Ребенок должен составить условие и вопрос, соответствующие данной схеме, а затем, используя цифры и арифметические знаки, выложить действие по решению задачи.

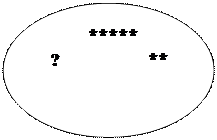
Рис. 36 Схемы к арифметическим задачам на сложение и вычитание

Примечание. Педагог использует при тестировании только те виды схем, с которыми дети знакомы из процесса обучения.

Тема урока: «Разложение чисел на простые множители».

Цель урока: выработать навык разложения чисел на простые множители, повторить признаки делимости чисел и использовать их при разложении чисел на простые множители, продолжать расширять представления учащихся об окружающем их мире.

ХОД УРОКА

Учитель: Добрый день, ребята. Садитесь. Откройте тетради и запишите число, классная работа. Тема нашего урока «Разложение чисел на простые множители».
Давайте вспомним, что это значит? Какие числа являются простыми? Какие еще вы знаете числа? К какой группе относится число 1? Теперь мы повторим, изученные нами, признаки делимости чисел на 3, 9, 5, 2 и 10. (Фронтально)

1) Работа в парах. Задание учащимся: заполнить таблицу:

«ш» 312 «ч» 310
«е» 567 «в» 585
«ы» 555 «б» 771

Ответ :

Историческая справка: Пафнутий Львович Чебышев – русский математик. Он занимался изучением свойств простых чисел. Он доказал, что между любым натуральным числом, большим 1, и числом, вдвое большим, всегда имеется не менее одного простого числа. Давайте проверим это на примере нескольких чисел. (Устно)

2) Задание учащимся: Соедините стрелками равные выражения, предварительно разложив числа из левого столбика на простые множители.

На доске записано:

125 2 . 2 . 2 . 2 . 7

315 5 . 5 . 5

444 2 . 2 . 3 . 13

112 2 . 2 . 3 . 37

156 3 . 3 . 5 . 7

Как по-другому можно записать выражения, стоящие в правом столбике?

24 . 7, 53, 22 . 3 . 13, 22 . 3 . 37, 32 . 5 . 7.

2) Проверьте правильность разложения чисел на простые множители, поставив знаки «+» или «–».

3) Задание учащимся: из чисел 84, 44, 75, 60 выберите то, которое раскладывается на наибольшее количество простых множителей. Подчеркните это число зеленым цветом.

4) Работа по группам

Задание учащимся: по разложениям чисел определите, какие из них делятся на 2, на 3, на 4, на 6, на 7:

1. 2 . 11 . 13
2. 2 . 5 . 3 . 17
3. 3 . 5 . 23 . 41
4. 2 . 2 . 2 . 3 . 7.

Выпишите отдельно разложения чисел, делящихся: на число 4; на число 6.

5) Отвечая на вопросы, впишите верные слова и в выделенном столбце получите имя ученого, математика, жившего до нашей эры.

1. Продолжите предложение: натуральное число, имеющее только два делителя называется …
2. Как называется натуральное число, на которое число а делится без остатка?
3. Какое число является делителем любого натурального числа?
4. Назовите автора первого учебника по математике.
5. Продолжите предложение: натуральное число, имеющее более двух делителей, называется …
6. Как называются числа, используемые при счете?

Ответы:

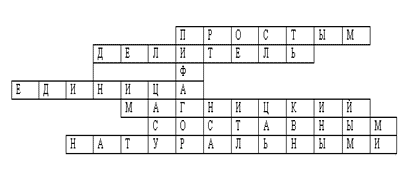
В данном кроссворде «спрятано» имя Пифагора Самосского (VI в. до н.э.). Историческая справка на эту тему: Пифагор и его ученики изучали вопросы делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, 6 = 1 + 2 + 3; 28 = 1 + 2 + 4 + 7 + 14; 496; 8 128.

Подведение итогов урока: Давайте подведем небольшой итог. Какова была цель урока? Мы её достигли?

Домашнее задание: п.41, № 495(3), №503, №507 (2).

Определение. Преобразование многочлена к виду произведения двух или нескольких многочленов ненулевой степени называется разложением многочлена на множители. Например: x2 – a2= (x – a)(x + a).

Рассмотрим различные приемы разложения многочленов на множители.

1) Способ гpyппировки и вынесение общего множителя за скобки.

При использовании этого способа иногда целесообразно применить "искусственные" преобразования - разбить отдельные члены на подобные слагаемые или ввести взаимно уничтожающиеся члены.

Пример 1. Разложить на множители многочлен a2 -2bc + 2ac - ab.

Решение. а2 – 2bс + 2ас ‑ ab= (а2 + 2ас) ‑ (2bс + ab) =

A (а + 2с) –b(2с + а) = (a + 2с)(a ‑ b).

Пример 2. Разложить на множители многочлен: х2 ‑ 3х + 2.

х2 ‑ 3х + 2 = х2 – х ‑ 2х + 2 = (х2 ‑ х) ‑- (2х ‑ 2) = х(х ‑ 1) ‑ 2(х ‑ 1) = (х ‑ 1)(х ‑ 2).

2) Применение формул сокращенного умножения. С помощью формул сокращенного умножения часто значительно облег­чается разложение на множители.

Пример 3. Разложить на множители многочлен: 5a5x3 + 5а2х9.

Решение. Сначала вынесем за скобки общий множитель 5a2х3, а затем применим формулу для суммы кубов:

5a5х3 + 5а2 х9 = 5а2х3(а3 + х6) = 5a2х3 (a3 + (х2)3) = 5a2x3(a+x2)(a2 ‑ ax2 +x4).

Пример 4. Разложить на множители многочлен Р(х) = х3 - 3х - 2.

Решение. Р(х) =х3 ‑ 3х ‑ 2 = х3 ‑ х ‑ 2х ‑ 2 = (х3 ‑ х) ‑ (2х+ 2) =

Х(х2 ‑ 1) ‑ 2(х+1) =х(х + 1)(х ‑ 1) ‑ 2(х + 1) = (х + 1)(х2 – х ‑ 2). Так как,

х2 ‑ х ‑ 2 = х2 ‑ х ‑ 1 ‑ 1 = (х2 ‑ 1) ‑ (х + 1) = (x+1)(x ‑ 1) ‑ (x+1)=(x+1)(x ‑ 2),

то P(x)=(x+1)2(x ‑ 2).

Иногда полезно выделение полного квадрата.

Пример 5. Разложить на множители х4+ 4.

х4 + 4 = х4 + 4х2 + 4 ‑ 4х2 = (х2 +2)2 - (2х)2 = (х2 +2х + 2)(х2 ‑ 2х + 2).

Для разложения на множители оказалось удачным выделение полного квадрата в выражении х4+4=(х2)2 + 22 (использована формула a2 + b2 = (а + b)2 ‑ 2ab.

3) Разложение квадратного трёхчлена на множители.

ах2 + bх + с = а(х – х0)(x ‑ х2); (а≠0,D = b2 ‑ 4ac≥0), где x1 и х2 – корни трехчлена ах2 + bх + с.

4) Разложение многочлена n-ой степени относительно х на множители.

Многочлен n-й степени относительно х имеет вид

Р(х) = аохп +a1xn-1 +...+аn-1x+аn,

где а0 ≠ 0, n ≥ 0 – целое число, а0, a1,..., аn – постоянные (коэффициенты многочлена), буква (величина) х может принимать любые числовые значения. Многочлен Р(х) записан в стандартном виде по убывающим степеням х.

Два многочлена Р(х) и P1(х) считаются равными: Р(х) = Р1(х),если при всех значениях х они принимают одинаковые значения.

Теорема Безу. При делении многочлена Рn(х) на двучлен (х-х0) получаем остаток R, равный значению многочлена при х =x0, т.е. R=Pn(x0).

Рn(x)=(х - х0)Qn-1 (х) + P(x0).

Следствия из теоремы Безу:

1. Если Рn(х) делится на (х ‑ х0) без остатка, т.е. R = 0, то х = х0 – корень многочлена Рn(x), т.е. Рn(x0) = 0.

2. Если х = х0 – корень многочлена Рn(x), т.е. Рn(х0) = 0, то Рn(х) делится на (х–х0) без остатка, т.е. Рn(x)=(х ‑ х0)Qn-1 (х)).

Обобщая, получим: Рn(x)=a0(х – х1) (x - x2)…(x ‑ xn), где x1, x2, …,xn – корни многочлена.

Пример 6. Разложить на множители многочлен

Р(х) = (х2 + х + 1)(х2 + х + 2) - 12.

Р(х) = (х2 + х + 1)((х2 +х + 1) + 1) ‑ 12 = (х2 +x + 1)2 + (х2 + х + 1) - 12.

Пусть x2 + х + 1=у. Тогда имеем у2 + y ‑ 12 = (у + 4) (у ‑ 3), так как корни трехчлена у2 + у ‑ 12 равны ‑ 4 и 3. Переходя от у к x, получаем

Р(х) = (х2 + х + 5) (х2 +x ‑ 2). Так как трехчлен x2 + х ‑ 2 = (х ‑ 1) (х + 2),

то Р(х) = (х ‑ 1) (х + 2) (х2 + х + 5).

Изучение приёмов преобразования уравнений начнём с обсуждения того, как можно разлагать на множители выражения, входящие в данное уравнение. Вообще представление уравнения f (x) = g (x) в виде F 1 (x) ċ F 2 (x) ċ ... ċ F n (x) = 0,

где выражения F k (x), k = 1, ..., n «проще» функций f (x) и g (x) , представляет собой несомненное продвижение в решении уравнения. В самом деле, представление вида (5) позволяет сразу приравнивать множители F k (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель) .

Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.

1. Вынесение общего множителя за скобку

В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена.

x 5 – 2x 3 + x 2 .

Каждое слагаемое этого многочлена содержит множитель x 2 . Вынесем его за скобку и получим ответ: x 5 – 2x 3 + x 2 = x 2 (x 3 – 2x + 1) .

2. Применение формул сокращённого умножения

Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы: a 2 - b 2 = (a - b) (a + b) , a 3 + b 3 = (a + b) (a 2 - a b + b 2) , a 3 - b 3 = (a - b) (a 2 + a b + b 2) , a 4 - b 4 = (a 2 - b 2) (a 2 + b 2) = (a - b) (a + b) (a 2 + b 2) , a 5 - b 5 = (a - b) (a 4 + a 3 b + a 2 b 2 + a b 3 + b 4) , a n - b n = (a - b) (a n - 1 + a n - 2 b + a n - 3 b 2 + a n - 4 b 3 + ... + a 2 b n - 3 + a b n - 2 + b n - 1) , n ∈ ℤ .

Разложить на множители многочлен (x – 2) 4 – (3x + 1) 4 .

Разложим разность четвёртых степеней по формуле, приведённой выше: (x - 2) 4 - (3 x + 1) 4 = ((x - 2) 2 - (3 x + 1) 2) ((x - 2) 2 + (3 x + 1) 2) = = (x - 2 - 3 x - 1) (x - 2 + 3 x + 1) (x 2 - 4 x + 4 + 9 x 2 + 6 x + 1) = = - (2 x + 3) (4 x - 1) (10 x 2 + 2 x + 5) .

3. Применение выделения полного квадрата

Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.

Разложить на множители многочлен x 4 + 4x 2 – 1 .

Имеем x 4 + 4 x 2 - 1 = x 4 + 2 ċ 2 ċ x 2 + 4 - 4 - 1 = (x 2 + 2) 2 - 5 = (x 2 + 2 - 5) (x 2 + 2 + 5) .

4. Группировка

Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель.

5. Метод неопределённых коэффициентов

Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной.

Теоретической основой метода являются следующие утверждения.

• Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
• Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
• Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Для доказательства второго утверждения вспомним, как выглядит график степенной функции с нечетной целой степенью (§ 2.2.5). Действительно, из его вида следует, что значение многочлена имеет разные знаки при x → +∞ и x → –∞ . Многочлен степени n – непрерывная функция, значит, найдется хотя бы одна точка, в которой график этой функции пересечет ось Ox .

Разложить на множители многочлен 3x 3 – x 2 – 3x + 1 .

Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax 2 + bx + c такие, что справедливо равенство 3x 3 – x 2 – 3x + 1 = (x – p)(ax 2 + bx + c) = ax 3 + (b – ap)x 2 + (c – bp)x – pc.

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырёх уравнений для определения четырёх неизвестных коэффициентов: { a = 3 b - a p = - 1 c - b p = - 3 - p c = 1 Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1.

Итак, многочлен 3x 3 – x 2 – 3x + 1 разлагается на множители: 3x 3 – x 2 – 3x + 1 = (x – 1)(3x 2 + 2x – 1).

6. Теорема о корнях многочлена

Разложение многочлена на множители иногда удаётся провести, если один из его корней угадан с помощью теоремы о рациональных корнях, доказанной в § 2.1.4 . После того, как корень x = α угадан, многочлен P n (x) представим в виде P n (x) = (x – α) ċ P n – 1 (x) , где P n – 1 (x) − многочлен степени на 1 меньше, чем P n (x) .

Разложить на множители многочлен x 3 – 5x 2 – 2x + 16 .

Данный многочлен имеет целые коэффициенты. По следствию теоремы о рациональных корнях (см. § 2.1.4) если целое число является корнем этого многочлена, то оно является делителем числа 16, то есть если у данного многочлена есть целые корни, то это могут быть только числа ±1, ±2, ±4, ±8, ±16.

Проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть x 3 – 5x 2 – 2x + 16 = (x – 2) ċ Q (x) , где Q (x) − многочлен второй степени. Следовательно, исходный многочлен разлагается на множители, один из которых (x – 2 ).

7. Разложение относительно параметра

Суть этого метода легче всего понять на примере.

Разложить на множители многочлен x 4 – 10x 2 – x + 20 .

Преобразуем данный многочлен: x 4 – 10x 2 – x + 20 = x 4 – 5 ċ 2x 2 – x + 25 – 5 = 25 – 5(1 + 2x 2) + x 4 – x

Рассмотрим теперь многочлен a 2 – a(1 + 2x 2) + x 4 – x , который при a = 5 совпадает с данным. Полученный многочлен является квадратным, его корни легко найти по теореме Виета: a 2 – a(1 + 2x 2) + x 4 – x = a 2 – a(1 + 2x 2) + x(x 3 – 1) = a 2 – a(1 + 2x 2) + x(x – 1)(x 2 + x + 1). Следовательно, a 1 = x(x – 1), a 2 = x 2 + x + 1 . Значит, исходный многочлен разлагается на множители a 2 – a(1 + 2x 2) + x 4 – x = (a – (x 2 – x))(a – (x 2 + x + 1)) . Вернемся к многочлену, данному в условии задачи, подставив a = 5 . Получим: x 4 – 10x 2 + x + 20 = (5 – x 2 + x)(5 – x 2 – x – 1) = (x 2 – x – 5)(x 2 + x – 4).