Ikki doira uchun umumiy tashqi tanangentning qurilishi. Ikki doira berilgan (demak, ularning markazlari O1 va O2 ham berilgan). Va ular uchun umumiy tashqi tangens, ya'ni bu doiralar uning bir tomonida yotadigan shunday bir tangensni qurish talab etiladi. Katta doira radiusi R deb nomlanadi, kichik doiraning radiusi r. Va birinchi navbatda, katta doira ichida biz bir xil markaz va radius atrofida (R-r) yordamchi doira quramiz. Keyin kichik doira markazidan yordamchi aylanaga yordamchi tangensni quramiz va kerakli tashqi tangens yordamchi tangensga parallel bo'ladi.

Birinchi yordamchi nurni A nuqtadan boshida ajratamiz. Katta aylananing radiusini kompas bilan o'lchaymiz va birinchi nurning boshidan xuddi shu kompas bilan AB segmentini R ga tenglashtiramiz. Endi kompas bilan kichik doiraning radiusini o'lchab, B segmentini B nuqtadan belgilaymiz. r ga teng. AC \u003d R - r ekan. Biz kompas bilan AC ni o'lchaymiz va xuddi shu kompas eritmasi bilan O1 markazida joylashgan birinchi yordamchi aylanani quramiz.

Endi O1 va O2 markazlarini segment bo'yicha bog'laymiz. Kompasning ixtiyoriy eritmasidan foydalanib, O1 markazi bo'lgan aylananing ikkinchi yordamchi yoyini quramiz. Va kompasning xuddi shu yechimi bilan biz aylananing uchinchi yordamchi yoyini O2 markazi bilan quramiz - shunday qilib uchinchi yoy ikkinchi nuqtani ikki nuqtada kesadi (biz ularni D va E deb ataymiz). Biz D va E ni o'rtada O1O2 bilan kesishgan segment orqali bog'laymiz - bu nuqtani F deb ataymiz. Endi kompas FO1 ni o'lchaymiz va ushbu kompas eritmasidan F1da O1O2 segmentida, diametri bo'yicha bo'lgan to'rtinchi yordamchi doirani chizamiz. Ushbu to'rtinchi doira birinchi yordamchi aylanani ikkita nuqtada kesishadi (ularni G va H deb nomlang). Ushbu ikkita nuqtadan biz eng yaxshi ko'rganlarini tanlaymiz (menga H nuqtasi yoqadi) va chiziqni O2 nuqtasi bilan bog'laymiz. HO2 chizig'i - bu kichik berilgan doiraning markazidan o'tadigan birinchi yordamchi doiraga bog'lovchi.

HO2 chizig'i kichik doirani ikki nuqtada kesadi (ularni K va L deb nomlang). Bu nuqtalar O2 ga teng va HO2 ga perpendikulyar hosil qilishimizga yordam beradi. O'zboshimchalik bilan kompas yechimidan foydalanib, biz aylantirilgan aylananing beshinchi yordamchi yoyini K. markaziga chizamiz. Xuddi shu kompas eritmasidan foydalanib, aylananing oltinchi yordamchi yoyini L markaziga qaratamiz - oltinchi yoy bir nuqtada beshinchisini kesishadi (M nuqtasi). Biz O2 va M ni chiziqqa bog'laymiz - bu chiziq (HO2 ga perpendikulyar) biroz kichikroq doirani bir nuqtada kesadi (biz uni N deb ataymiz).

Endi N orqali biz yordamchi HO2 tangensiga parallel ravishda chiziq chizamiz. O'zboshimchalik bilan kompas eritmasidan foydalanib, biz N nuqtada joylashgan ettinchi yordamchi doira quramiz - shunday qilib, ettinchi doira HO2 ni ikkita nuqtada kesishadi (biz P va Q nuqtalarni chaqiramiz). Kompasning xuddi shu yechimidan foydalanib, P ga markazlashtirilgan sakkizinchi yordamchi aylanani quramiz va sakkizinchi doira HO2 yordamchi tangensni ikkita nuqtada kesishadi (nuqtalar Z va S deyiladi). Kompasning xuddi shu yechimidan foydalanib, to'qqizinchi yordamchi yoyni Z markazida aylantiramiz, shunda to'qqizinchi yoy ettinchi aylanani biron bir nuqtada kesadi (biz T nuqtasini chaqiramiz). N va T chiziqlarni ulang - bu NT chizig'i ushbu ikki aylanaga zarur bo'lgan umumiy tashqi tanangents bo'ladi.

Va shuning uchun: NT aylana bo'ylab yotgan O2N radiusidan o'tadi. Bundan tashqari, qurilish orqali NT HO2 ga parallel va O2N radiusiga perpendikulyar bo'ladi - shuning uchun NT kichik berilgan doiraga tegadi. Endi O1H radiusini oling va uni TN chizig'i bilan kesishishga qadar uzating (kesishish nuqtasi U deb nomlanadi). O1H radiusi O2H tangensiga perpendikulyar - bu O2HU burchagi to'g'ri chiziq ekanligini anglatadi. Aniqlanishicha, to'rtburchaklar UHO2N uchta to'g'ri burchakka ega - bu HUN to'rtinchi burchagi to'g'ri chiziq, UHO2N esa to'rtburchak bo'lib, HU tomoni O2N ning qarama-qarshi tomoniga teng, ya'ni radius r. Endi biz O1U (O1H va HU dan iborat) segmentning uzunligini topamiz. Uzunlik O1H va HU uzunliklarining yig'indisiga teng, ya'ni (R - r) + r \u003d R. Ma'lumki, U O1 dan R bilan ajratilgan, ya'ni U katta berilgan doirada yotadi, ya'ni TN U orqali o'tib, - Aylanada yotgan O1U radiusining uchidan o'tadi va radiusga perpendikulyar bo'ladi, ya'ni TN bu berilgan katta doiraga teguvchi. Qurilish tugallandi.

O'xshashlik, aylanish, parallel tarjima, inversiya va kartografik proektsiyalar kabi. Texnik nuqtai nazardan, bu o'zgarishlar, chiziqlar va doiralarning o'zlari deformatsiyaga uchragan bo'lsa ham, tangens chiziqlari va doiralarining tarqalish tuzilishini o'zgartirmaydi.

Tanglik nuqtasi orqali chizilgan aylananing radiusi tangens chizig'iga perpendikulyar. Va aksincha, so'nggi nuqtada (aylanada) radiusga perpendikulyar bo'lgan tanang chiziq. Tangens chizig'i bilan aylana radiusga nisbatan (tangens nuqtasiga qadar) eksenel simmetriyaga ega.

Doira ichidagi nuqta orqali biron bir tangens chizig'i o'tishi mumkin emas, chunki har qanday chiziq ajratilgan bo'lishi kerak. Shu bilan birga, doiradan tashqarida joylashgan har qanday nuqta uchun biz uning ichidan o'tadigan ikkita tangens chizig'ini qurishimiz mumkin. Doira va ikkita tanangent chiziqdan iborat geometrik shakl, shuningdek, nuqtani bog'laydigan chiziqqa nisbatan eksenel simmetriyaga ega. P  markaziy doira O  (o'ngdagi rasmga qarang). Bunday holda, segmentlar nuqtadan P  ikki tagacha aloqa nuqtalari bir xil uzunlikka ega. Nuqtali daraja teoremasi bo'yicha kesma uzunligining tanangentsiya nuqtasiga bo'lgan kvadrati aylanaga nisbatan P nuqta darajasiga tengdir. C. Bu daraja nuqta orasidagi masofalar mahsulotiga tengdir. P  har qanday kesish chizig'i bilan aylananing kesishgan ikki nuqtasiga P.

Tangens chizig'i t  va teginish nuqtasi T  bir-biriga uyg'unlashuv xususiyatiga ega bo'lish; bu yozishmalarni qutb va qutb g'oyalari bo'yicha umumlashtirish mumkin. Xuddi shu munosabatlar nuqta o'rtasida mavjud P  doiradan tashqarida va tangensiyaning ikki nuqtasini bog'laydigan kesilgan chiziqda.

Agar P nuqta O markazi bilan aylana tashqarisida bo'lsa va P dan tangens chiziqlar T va S nuqtalaridagi aylanaga tegsa, u holda PSTPS va ∠TOS burchaklari 180 ° ga qo'shiladi.

Ushbu teorema va uning teskari tomonlari turli xil dasturlarga ega. Masalan, u teoremadan darhol aylana hech qanday to'rtburchaklar ichiga yozilishi mumkin emasligini, agar u kvadrat bo'lmasa va doirani biron bir rombga yozib qo'yish mumkin bo'lsa ham, umumiy holatda aylanani parallelogrammaga yozib bo'lmaydi, degan xulosaga keladi.

Ikki aylana bo'ylab tangens chiziqlar[ | ]

Ikki doira uchun, umumiy holatda, agar bitta doira ikkinchisida yotmasa, ikkala aylana uchun to'rtta turli xil chiziqlar bo'ladi, ammo buzilgan holatlarda noldan to'rtgacha bo'lgan har qanday sonli tangens bo'lishi mumkin. Ushbu holatlar quyida tasvirlangan. To'rtta tangens chiziqlaridan ikkitasi, aylanalar tangens chizig'ining bir tomonida yotganda tashqi tangensdir. Boshqa ikkita chiziq uchun ichki tanjents, doiralar tangens chizig'ining qarama-qarshi tomonlarida yotadi. Tashqi tangenslar markazda kesishadi tashqi homotetiya, ichki tanjentsiyalar ichki gomotetaning markazida kesishadi. Homotetiyaning ichki va tashqi markazlari kichik doira markaziga yaqinroq bo'lgan doiralar markazidan o'tgan to'g'ri chiziqda yotadi. Agar ikkita aylana bir xil radiusga ega bo'lsa, xuddi shu to'rtta tangents qoladi, ammo tashqi tanangentsiya chiziqlari parallel va affin tekisligida homotetiyaning tashqi markazi yo'q. Proektsion tekislikda homotetiyaning tashqi markazi chiziqlar kesishishiga to'g'ri keladigan cheksiz uzoqroq nuqtada joylashgan.

Tashqi tanangent[ | ]

Nuqtalarni bog'laydigan qizil chiziqlar T  1 va T 3 , T  2 va T  4 - bu ikki doiraning tashqi tangenslari.

Ichki tangents[ | ]

Ichki tangentslar - aylana markazlarini bog'laydigan chiziq bilan kesishadigan tangents. E'tibor bering, ichki aylanalar kesishgan holatlarda mavjud emas.

Bino [ | ]

Ikki doira uchun tirgaklar yuqorida aytib o'tilganidek, homotetiya markazlarini topish va shu markazlardan o'tgan tangenslarni qurish orqali qurilishi mumkin. Bundan tashqari, quyida tavsiflangan to'g'ridan-to'g'ri tangens chiziqlari va tangens nuqtalarini qurish mumkin.

Boshlang'ich geometriya[ | ]

Ruxsat bering O  1 va O  2 - ikkita aylananing ikkita markazi C  1 va C  2 va ruxsat bering r  1 va r  2 - ularning radiusi, shu bilan birga r 1 > r  2. Boshqacha aytganda, aylana C  1, biz ikki doiraning eng kattasini ko'rib chiqamiz. Tashqi va ichki tangens chiziqlarini qurish uchun ikki xil usuldan foydalanish mumkin.

Tashqi tangenslar

Yangi doira chizish C  3 radiusi bilan r 1 − r  2 markazda O O  2 bu yangi davraga. Ushbu chiziqlar istalgan tanang chiziqlariga paralleldir, chunki bu ikkala doiraning radiusining pasayishiga to'g'ri keladi C  1 va C  2 bir xil raqamga r  2, natijada doira C  2 nuqta aylanadi. Doiradagi ikkita tangens nuqtalari orqali C  3 siz markazdan ikkita nurni chizishingiz mumkin O  1. Bu nurlar kesishadi C 1 kerakli teginish nuqtalarida. Kerakli tangenslar ushbu radial nurlarga perpendikulyar bo'lib, yuqorida ko'rsatilgandek qurilishi mumkin.

Ichki tangentsiyalar

Yangi doira chizish C  3 radiusi bilan r 1 + r  2 markazda O  1. Yuqorida tavsiflangan usuldan foydalanib, nuqtadan ikkita tangens chizig'ini torting O  2 bu yangi davraga. Ushbu chiziqlar kerakli tanang chiziqlariga paralleldir, chunki bu aylana radiusining pasayishiga to'g'ri keladi C  Radiusni oshirganda 2 dan nolgacha C  1 bir xil doimiyga r  2. Markazdan ikkita radial nurni tortish mumkin O  1 teginish nuqtalari orqali yoqish C  3. Bu nurlar kesishadi C  1 kerakli teginish nuqtalarida. Kerakli ichki tirgaklar radial nurlarga perpendikulyar bo'lib, yuqorida ko'rsatilgan usul bilan qurilishi uchun nurlarni topilgan nuqtalarda kesishadi.

Aslida, bu tashqi aylanishlar bilan bir xil qurilish, agar biz kichik doira radiusi manfiy deb hisoblasak.

Analitik geometriya[ | ]

Davralarning markazlari bo'lsin v 1 = (x 1 ,y  1) va v 2 = (x 2 ,y  2) va radius r  1 va r  Mos ravishda 2. Tangens chizig'i tenglamaga ega bo'lsin    a x + b y + c \u003d 0, (\\ displey uslubi oqi + tomonidan + c \u003d 0,)  normallashtirish bilan a 2 + b  2 \u003d 1, keyin doira markazlaridan chiziqgacha bo'lgan masofa formulalar yordamida hisoblanadi:

bolta 1 + tomonidan 1 + v = r  1 va bolta 2 + tomonidan 2 + v = r 2 .

Ikkinchisidan birinchi tenglamani ayting, biz olamiz

aΔ x + bΔ y = Δ r

qaerda Δ x = x 2 − x  1, Δ y = y 2 − y  1 va Δ r = r 2 − r 1 .

Agar    d \u003d (Δ x) 2 + (Δ y) 2 (\\ displaystyle d \u003d (\\ sqrt ((\\ Delta x) ^ (2) + (\\ Delta y) ^ (2))))  - masofa v  1 ga v  2, almashtirish orqali biz normalizatsiya qilishimiz mumkin X = Δ x/d, Y = Δ y/d  va R = Δ r/d  tenglamalarni beradigan tenglamalarni soddalashtirish aX + bY = R  va a 2 + b  2 \u003d 1. Biz ularni echamiz va ikkita echimni olamiz ( k  \u003d ± 1) ikkita tashqi tangens chiziqlar uchun:

a = Rx − kY√(1 − R 2) b = Ry + kX√(1 − R 2) v = r 1 − (bolta 1 + tomonidan 1)

Geometrik jihatdan, bu tangens va markazlar orqali chizilgan to'g'ri chiziq hosil qilgan burchakni hisoblashga to'g'ri keladi va keyin tangens tenglamasini olish uchun tsentral chiziq aylantiriladi. Burchakni to'g'ri uchburchakdan hisoblash mumkin, uning uchlari homotetiyaning (tashqi) markazi, aylananing markazi va tananglik nuqtasidir. Gipotenuza markazlarning to'g'ri chizig'ida yotadi, radius - oyoq, burchakka qarama-qarshi va burchakka ulashgan oyoq tanang chizig'ida yotadi.

(X, Y) yo'naltirilgan birlik vektor v  1 in v  2, esa R  ga teng    cos \u2061 θ (\\ displaystyle \\ cos \\ theta)markazlar chizig'i va tangens o'rtasidagi burchak qaerda.    sin \u2061 θ (\\ displaystyle \\ sin \\ theta)  keyin teng    ± 1 - R 2 (\\ displaystyle \\ pm (\\ sqrt (1-R ^ (2)))))  (belgiga qarab)    θ (\\ displaystyle \\ theta), bu aylanish yo'nalishiga teng) va yuqoridagi tenglamalar aylanish ( X, Y) yoqilgan    ± θ, (\\ displey uslubi \\ pm \\ theta,)  aylanish matritsasi yordamida

   (R ∓ 1 - R 2 ± 1 - R 2 R) (\\ displaystyle (\\ start (pmatrix)) Ar-ge / mp (\\ sqrt (1-R ^ (2))) \\\\\\ pm (\\ sqrt (1-R) ^ (2))) & R \\ end (pmatiks))) k  \u003d 1 - aylanalarning o'ng tomonidagi tangens chizig'i v  1 tomonga v 2 . k  \u003d −1 - aylanalarning o'ng tomonidagi tangens chizig'i, ko'rinib turibdiki v  2 tomonga v 1 .

Yuqoridagi barcha dalillar aylanalarning radiusi ijobiy ekanligidan dalolat beradi. Agar r  1 ijobiy, va r  2 manfiy bo'ladi v  1 har bir satrning chap tomonida yotadi va v  2 - o'ngda va ikkita tangens chiziqlar kesishadi. Shu tarzda siz barcha to'rtta echimni olishingiz mumkin. Ikkala radiusning belgisini o'zgartirish variantlarni almashishga olib keladi k  \u003d 1 va k = −1.

Vektorlar [ | ]

Umumiy teginish nuqtalari t  1 va t  Ikkala to'rtburchak chiziqlardan har biri uchun markazlari bo'lgan doiralarga v  1 va v  2 va radii bilan r  1 va r  2 to'rtta tenglamani yechish orqali olinadi:

   (t 2 - v 2) ⋅ (t 2 - t 1) \u003d 0 (t 1 - v 1) ⋅ (t 2 - t 1) \u003d 0 (t 1 - v 1) ⋅ (t 1 - v 1) \u003d r 1 2 (t 2 - v 2) ⋅ (t 2 - v 2) \u003d r 2 2 (\\ displey uslubi (\\ boshlanadi (tekislanadi)) (t_ (2) -v_ (2)) \\ cdot (t_ (2) - t_ (1)) & \u003d 0 \\\\ (t_ (1) -v_ (1)) \\ cdot (t_ (2) -t_ (1)) & \u003d 0 \\\\ (t_ (1) -v_ (1)) \\ cdot (t_ (1) -v_ (1)) & \u003d r_ (1) ^ (2) \\\\ (t_ (2) -v_ (2)) \\ cdot (t_ (2) -v_ (2)) &; \u003d r_ (2) ^ (2) \\\\\\ oxiri (tekislangan)))

Ushbu tenglamalar, tangens chizig'i radiusga perpendikulyar ekanligi va tanangent nuqtalar mos keladigan doiralarda yotganligini anglatadi.

Ikki o'lchovli vektorli o'zgaruvchilarga ega bo'lgan ushbu to'rtburchaklar tenglamalari odatda to'rt juft echimlarni beradi.

Vaziyatning yomonlashuvi[ | ]

Ikki xil aylana, noldan to'rtta to'g'ri chiziqqa, nisbiy holatga qarab, ikkala doiraga tegishi mumkin. Variantlarni markazlar va nurlar orasidagi masofaga qarab tasniflash mumkin.

Va nihoyat, agar doiralar bir-biriga to'g'ri kelsa, bitta aylananing har qanday tangens chizig'i umumiy tangens bo'ladi.

Bundan tashqari, umumiy tangens chizig'i tushunchasini manfiy radiusli doiralar misolida (bir xil nuqtalardan hosil bo'lgan doiralar) keltirish mumkin.    x 2 + y 2 \u003d (- r) 2, (\\ displey uslubi x ^ (2) + y ^ (2) \u003d (- r) ^ (2),)lekin "tashqarida"). Bunday holda, agar radiuslar qarama-qarshi belgilarga ega bo'lsa (bir doira ijobiy radiusga, ikkinchisi salbiy), homotitning tashqi va ichki markazlari o'zgaradi va tashqi va ichki umumiy tangentslar joylarni o'zgartiradi. Agar radius bir xil belgiga ega bo'lsa (ikkalasi ham musbat, ham manfiy), u holda “tashqi” va “ichki” tushunchalari odatiy ma'noga ega.

Nol radiusli doiralar uchun umumiy tangenslarni aniqlash mumkin. Bunday holda, nol radiusli doira qo'shaloq nuqta sifatida ko'rib chiqiladi va shuning uchun bu nuqta orqali o'tadigan har qanday chiziq uni kesib o'tadi. ko'payish  ikki. Agar aylana nol radiusiga ega bo'lsa, umumiy tanganent chizig'i shunchaki nuqta orqali aylanaga bog'laydigan chiziqdir, ammo bu chiziq ikki marta ko'rib chiqiladi. Agar ikkala aylana ham nol radiusga ega bo'lsa, u holda umumiy tangens chizig'i ikki nuqta orqali o'tadigan chiziqdir va bu chiziq to'rtlik ko'paytmasiga ega.

E'tibor bering, ushbu buzilgan holatlarda, homotetiyaning tashqi va ichki markazlari qoladi (agar tashqi radius teng bo'lsa, tashqi markaz cheksizlikka ketadi), agar doiralar bir-biriga mos kelmasa (bu holda tashqi markaz aniqlanmagan) yoki ikkala doiraning nol radiusi bo'lsa ( bu holda ichki markaz yo'q).

Ilovalar [ | ]

Kamar haydash muammosi[ | ]

Ichki va tashqi tangenslar hal qilishda foydalidir kamar haydovchi vazifalari , tishli g'ildiraklarga mahkam o'rnashadigan kamar uzunligini hisoblashdan iborat. Agar biz kamarni ahamiyatsiz qalinligi bo'lgan matematik egri deb hisoblasak va uzatish g'ildiraklari aynan bir tekislikda bo'lsa, muammo kamarning mos keladigan uzunliklari bilan tangenslarning segmentlarini yig'ishda kamayadi. Agar kamar g'ildiraklar bilan kesishgan holda tortilsa, ichki tangenslarni hisobga olish kerak. Agar bilaguzuk kesishmasdan tortilgan bo'lsa, tashqi tangalarni hisobga olish kerak. Ikkinchi holat ba'zan chaqiriladi kasnaq vazifasi.

Uchta aylana bo'ylab harakatlanuvchi chiziqlar: Mong teoremasi[ | ]

Uchta doira uchun C 1 , C  2 va C  3 uchta aylana bor ( C 1 C 2 , C 2 C  3 va C 1 C  3). Har bir juft doirada ikkita homotetiya markazi bo'lganligi sababli, biz oltitadan olamiz homotety markazlari. Gaspard Mong 19-asr boshlarida bu oltita nuqta to'rtta satrda yotishini va har bir satrda uchta nuqta borligini ko'rsatdi.

Tangent chiziqlar va bilyard[ | ]

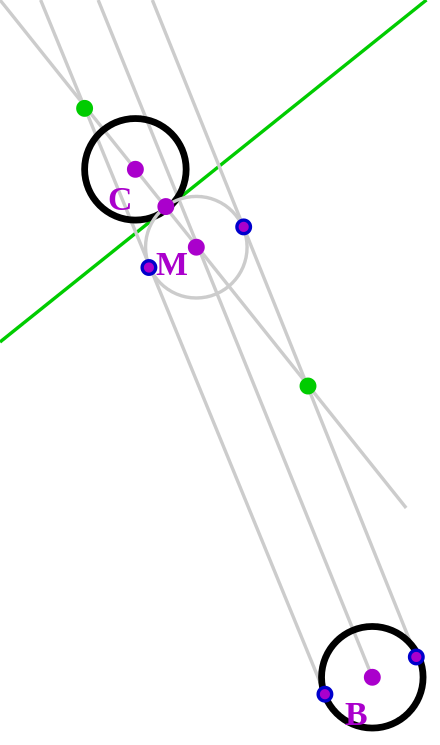
Maqsad bilyardda. Koptok to'pidan ta'sir qilish yo'nalishi (B to'pi) aloqa nuqtasi cho'ntakning o'rtasidan va nishon to'pining o'rtasidan o'tadigan chiziqning kesishish nuqtasiga to'g'ri kelishi uchun tanlanadi. Bu holda maqsadli to'p cho'ntagiga qarab yo'naltiriladi va replikatsiya to'pi (C) va xayoliy to'pga (M) tegib turgan yashil chiziqqa parallel bo'ladi.

Tyuning balli tangentli chiziq tizimi, repetitorning to'pi orqali yo'naltiriladigan to'p yo'nalishi bo'yicha ikkita tangens chizig'ini yaratish uchun, o'rtaning o'rtasidan to'g'ri chiziqdan foydalanadi. Ikki tangens chizig'i va kupe to'pining o'rtasidan o'tadigan to'g'ri chiziq nishon to'pi o'rtasidan va cho'ntagining o'rtasidan o'tgan to'g'ri chiziq bilan kesishadi. Shiqillagan to'pning oxirgi holati (rasmdagi xayoliy to'p) aloqa nuqtasida mo'ljal qilingan to'pni cho'ntagiga yo'nalgan tomonga perpendikulyar bo'lgan to'g'ri chiziqqa tegishi uchun urish kerak (rasmda bu tangents yashil rang bilan ajratilgan).

Ob'ektlarning konturlarini chizishda, ko'pincha ikki aylana yoyiga umumiy tangenslarni qurish kerak bo'ladi. Ikki doira uchun umumiy bo'lgan tangens tashqi bo'lishi mumkin, agar ikkala doira ham uning bir tomonida joylashgan bo'lsa va ichki, agar doiralar tangensning turli tomonlarida joylashgan bo'lsa.

R va r radiusi bo'lgan ikki doiraga umumiy tashqi tanangentsning qurilishi (47-rasm). Katta radiusli doira markazidan - nuqtalar O 1 radius doirasini tavsiflang R – r (47-rasm, a). Segmentning o'rtasini toping O 2 O 1 – nuqta O 3   va undan yordamchi radius doirasini chizamiz O 3 O 2 yoki O 3 O 1.   Ikkala chizilgan doiralar nuqtalarda kesishadi A va Ichida . Ballar O 1 va B to'g'ri chiziqni va uning kesishmasida radius doirasi bilan ulang R teginish nuqtasini aniqlang D (47-rasm, b). Nuqtadan O 2   to'g'ri tekislikka parallel O 1 D radius aylanasi bilan kesishishga to'g'ri chiziq torting r va ikkinchi teginish nuqtasini oling C . To'g'ridan-to'g'ri CD qidirilayotgan tangens. Ushbu doiralar uchun ikkinchi umumiy tashqi tangens ham qurilgan (chiziq) Ef ).

47-rasm

R va r radiusining ikki doirasiga umumiy ichki tanangentsning qurilishi (48-rasm). Har qanday doiraning markazidan, masalan: nuqtalar O 1   , radius doirasini tasvirlang R +r (48-rasm, a). Chiziqni ajratish O 2 O 1 yarmida, nuqta oling O 3   . Nuqtadan O 3   radiusli ikkinchi yordamchi doira qanday O 3 O 2   \u003d O 3 Oh 1   va fikrlarni belgilang A va Ichida   yordamchi doiralarning kesishishi. To'g'ri nuqtalarni ulash A va O 1 (Rasm 48, b), uning radiusi aylanasi bilan kesishgan joyda R teginish nuqtasini oling D . Radius doirasining markazi orqali r chiziqqa parallel ravishda chiziq chizing O 1 D , va berilgan aylana bilan uning kesishishida ikkinchi aloqa nuqtasini aniqlang Bilan . To'g'ridan-to'g'ri CD – berilgan aylanalarga ichki tangens. Ikkinchi tangens ham xuddi shunday qurilgan. Ef .

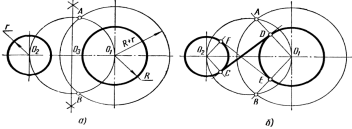
48-rasm

3.3 Dairesel kamondan foydalanadigan turmush o'rtoqlar

3.3.1 Ikkala to'g'ri chiziqni aylana yoyi bilan birlashtirish

Arkni konjugatsiya qilish uchun barcha vazifalarni ikki turga qisqartirish mumkin. Ulanish juftlashma yoyining berilgan radiusi orqali yoki juftlashish chizig'ining birida aniqlangan nuqta orqali amalga oshiriladi. Ikkala holatda ham juftlashuvchi yoyning o'rtasini qurish kerak.

Berilgan radiusi R ga teng bo'lgan ikkita kesishgan to'g'ri chiziqlarni yoy bilan birlashtirish v (49-rasm, a). Birlashtiruvchi kamon berilgan chiziqlarga tegishi kerakligi sababli, uning markazini har bir chiziqdan radiusga teng miqdorda olib tashlash kerak. R v   . Juftlashtirish shunga o'xshash tarzda qurilgan. Berilgan tomonga parallel ravishda ikkita to'g'ri chiziq chiziladi va ulardan radius bilan masofada joylashgan R v   va bu chiziqlar kesishgan joyida nuqta belgilanadi O – juftlashgan yoyning markazi. Nuqtadan Oh berilgan satrlarning har biriga perpendikulyar tushiring. Perpendikulyar asoslar - nuqtalar A va B – juftlashgan yoyning tangens nuqtalari. Ushbu konjugatsiya qurilishi har qanday burchakni tashkil etuvchi ikkita kesishgan tekis chiziqlar uchun amal qiladi. To'g'ri burchakning yon tomonlarini birlashtirish uchun siz 49, b rasmda ko'rsatilgan usuldan ham foydalanishingiz mumkin.

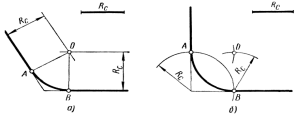
49-rasm

Ikkita kesishgan to'g'ri chiziqlarning konjugatsiyasi, ularning birida birlashtiruvchi yoyning A tanang nuqta berilgan. (50-rasm). Ma'lumki, ikkita kesishuvchi chiziqlarni bog'laydigan yoy markazlarining geometrik joylashuvi bu chiziqlar hosil qilgan burchakning bisektoridir. Shuning uchun, burchakning bisektorini tejamkorlik nuqtai nazaridan qurish A bisektor bilan kesishguncha chiziqqa perpendikulyar tiklang va nuqtani belgilang O – juftlashgan yoyning markazi. Nuqtadan voz kechish Oh   boshqa to'g'ri chiziqqa perpendikulyar ravishda B tanosilligining ikkinchi nuqtasini va radiusni oling R v \u003d OA \u003d OB   ikkita chiziqni bir-biriga bog'lang, ularning biriga teginish nuqtasi o'rnatildi.

Berilgan A tanangentsiya nuqtasidan o'tuvchi yoy orqali ikkita parallel chiziqlarning konyugatsiyasi (51-rasm). Nuqtadan A berilgan chiziqlarga perpendikulyar tiklang va ikkinchi chiziq bilan kesishgan nuqtani belgilang B . Chiziq segmenti Ab yarmiga bo'ling va nuqta oling Oh Birlashgan radius markazining markazi.

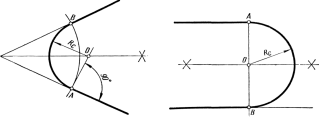
50-rasm 51-rasm