Let us now consider a few more complex constructive problems. Let's start by building regular decagon. Suppose that a regular decagon is inscribed in a circle of radius 1 (Fig. 32); we denote its side by x. Since the central angle at which this side x is visible from the center of the circle contains 36 °, the other two angles of the large triangle each contain 72 °, and therefore, the dashed line dividing the angle A in half divides the triangle OAB into two isosceles triangles with equal sides of length x. The radius of the circle, therefore, is composed of segments x and 1 x. Since the triangle OAB is similar to the smaller of the two triangles into which it is divided, we get This proportion leads to the quadratic equation x 2 + x - 1 \u003d 0, whose solution has the form 
(We are not interested in another solution, since it corresponds to a negative value x.) From the obtained formula it is clear that the segment x can be built geometrically. Having the same segment x, we can build a regular decagon, laying around the circumference ten times the chord x. From here it is already easy to get a regular pentagon, connecting the vertices of the decagon through one.
Instead of constructing √5 with the method indicated in Fig. 31, we can also construct the hypotenuse of a right-angled triangle with sides 1 and 2. Then we will have to subtract a single segment and divide what we have in half.
The relation in the considered problem was called "golden", since, according to Greek mathematicians, the rectangle, the sides of which are in this respect, is aesthetically especially pleasing to the eye. The ratio is approximately 1.62.
Of all regular polygons the easiest way to build a hexagon. Since the length of the side of such a hexagon inscribed in a circle is equal to the radius of the circle, the hexagon itself is constructed without difficulty if we put aside six times the circumference of a segment equal to the radius.
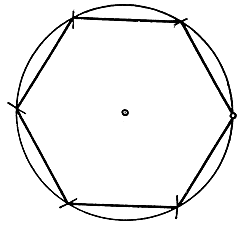
Having a regular n-gon, you can immediately get a regular 2n-gon, halving the arcs between adjacent vertices of the n-gon. Starting with the diameter of the circle (a regular inscribed "diagon"), we construct successively 4, 8, 16, ..., 2 n -gons. In the same way, starting with the hexagon, we get 12, 24, 48, ... -gons, and starting with the “decagon,” we get the 20, 40, ... -gons.
If s n denotes the length of the side of a regular n-gon inscribed in a unit circle (i.e., a circle with radius 1), then the side of a regular inscribed 2n-gon will have length
This is proved as follows (Fig. 34): s n \u003d DE \u003d 2DC, s 2n \u003d DB and AB \u003d 2. The area of \u200b\u200bthe right triangle ABD is equal to or, on the other hand, Since 
then, substituting and comparing two expressions for the area, we get:
It remains to solve the quadratic equation for x \u003d s 2 2n and, when choosing the root, take into account that x must be less than 2.
From this formula, since the length of S 4 (the side of the square) is √2, it follows that
As a general formula, we obtain (for n\u003e 2).
Task 1: How to cut a 4 × 9 rectangle into two parts so that a square can be folded from them? Decision: Task 2: A circle is given and a point inside it is marked. What is the minimum number of parts you can cut this circle so that from the resulting parts you can add a circle in which the marked point is the center. Decision: Cut a circle with a diameter of AO (or rather a little more) and rotate it 180. Task 3: Cut a corner made up of three cells () into four equally shaped parts. Task 4: Using cuts and shifting, make the figure “candy” from the “cross” figure (see figure).
a) using cuts and shifting;
b) using only cuts. Decision:
Task 7: a) Is it possible to cut a square into 100 equal quadrangles that are not rectangles? b) Is it possible to cut a square into 2000 equal triangles? Task 8: Is it possible to add a square of figures? Figures can be taken in unlimited quantities. And if the long side of the corner is equal to n cells? Task 9: Is it possible to bridge a plane with the same a) pentagons; b) hexagons; c) heptagons? Task 10: Cut the square into two identical a) pentagons; b) hexagon; c) 2n-gon; d) 2n + 1-gon. Is it possible to cut a rectangle like this? What other shapes is this algorithm suitable for? Task 11: Is it possible to cut into four acute-angled triangles a) some pentagon; b) a regular pentagon? Task 12:The pictures show figures on checkered paper. Your task is to cut each figure into two identical (in shape and size) parts.
Different cutting tasksGrade 7 - 2011
Cut the rectangle with sides 4 and 9 into the smallest number of parts so that to make a square out of them.
Task
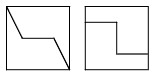
You can easily cut a square into two equal triangles or two equal quadrangles. But how to cut a square into two equal pentagons or two equal hexagons?
hint
Consider whether the polygons you are looking for are convex.
Decision
Of course, the desired polygons cannot be convex. One possible solution is shown in the figure.
Answer: See picture.
Task
Cut the square into 3 parts, from which you can fold a triangle with 3 sharp corners and three different sides.
Decision
See the picture: the square is cut into three parts: white, turquoise and green.
Task
Is it possible to bake a cake that can be divided into 4 parts in one straight cut?
hint
Note that the cake does not have to be a convex figure.
Decision
If the cake was a convex figure, this would not have been possible, but it’s not said anywhere that it should be like that. You can, for example, bake a cake in the form of the letter "W" and cut it as shown in the figure.
Answer: See picture.
Task
Two people had two square cakes. Each made on his cake 2 straight cuts from edge to edge. At the same time, one got three pieces, and the other four. How could this be?
hint
Please note, cuts may intersect.
Decision
This could happen if in the first case the sections did not intersect, and in the second they intersected. For example, if in the first case they were parallel to each other, and in the second - perpendicular.
Task
Cut the square into three parts, from which you can fold a triangle with three sharp corners and three different sides.
Answer: See the picture (equal parts are shaded the same way).
Task
Cut the figure in the left figure into two identical parts.
Answer: See picture.
Task
Cut the figure in the figure into two parts, from which you can fold a triangle.
Answer: See picture.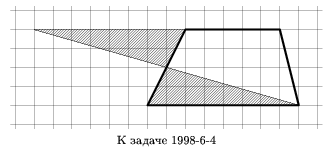 
Task
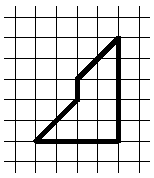
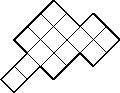
Kai has an ice plate in the shape of a “corner” (see. Figure). The Snow Queen demanded that Kai cut it into four equal parts. How can he do this?
Decision
It is necessary to cut this corner into four small corners as shown in the figure:
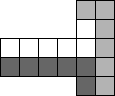
Task
Cut the figure (see the figure) into two identical (coincident when overlapping) parts.
Task
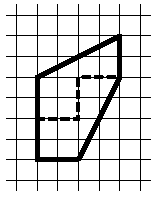
Cut the figure in the figure into two equal parts.
Decision
Task
Cut this shape (see the figure) into three equal shapes.
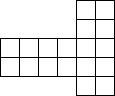
Decision
The initial figure consists of eighteen cells, therefore, each of the three figures into which it is necessary to divide it should consist of six cells. By searching, we establish that 5 cells of the desired figure should lie in the same row.
Task
Cut the corner shown in the figure into four of the same corners half the size.
Decision
Task
The Magic Land has its own magical laws of nature, one of which says: "A carpet-carpet will fly only when it has a rectangular shape." Ivan Tsarevich had a 9 × 12 carpet plane. Once, the Serpent Gorynych crept up and cut a small rug 1 × 8 from this carpet. Ivan Tsarevich was very upset and wanted to cut another piece of 1 × 4 to get an 8 × 12 rectangle, but Vasilisa the Wise suggested doing something different. She cut the carpet into three parts, of which a 10 × 10 square carpet rug was sewn with magic thread. Can you guess how Vasilisa the Wise remade a damaged carpet?
hint
Think about how the carpet-plane began to look after the Serpent Gorynych cut a piece from it.
Decision
After the Serpent Gorynych ruined the carpet, Ivan Tsarevich could cut a piece of 1x4 from this carpet and turn it into an 8 × 12 carpet. This means that after the departure of the Serpent Gorynych, the carpet looked as shown in Fig. 1. Vasilisa the Wise cut this carpet as shown in fig. 2, and sewn as shown in Fig. 3.
Task
Cut the pentagon shown in the figure into two identical (coincident when overlapping) parts.
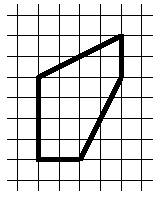
Task
Pete and Kolya were given two identical figures cut out of checkered paper. It is known that in each figure less than 16 cells. Petya cut his figure into pieces of four cells (see the figure on the left), and Kolya cut his figure into corners of three cells (see the figure on the right). Give an example of a figure that could give the boys. Show how Petya cut this figure into pieces, and how Kolya cut it.
Decision
From the conditions of the problem it follows that the desired figure should consist of 12 cells. Three possible shapes and methods of cutting them are shown in the figure.
Task
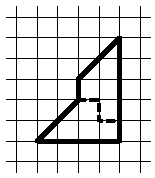
When Kai completed this task, the Queen gave him another ice plate (see. Figure). How to cut it into two equal parts?
Decision
See picture:
Task
Can a 2 * 2 square sheet of paper be folded so that it can be cut into 4 1 * 1 squares with one wave of scissors?
hint
Adding a square is allowed not only along grid lines.
Decision
Fold the square in half diagonally, and then the resulting isosceles right triangle - again in half (see picture). Now all 4 segments of length 1, along which you need to cut a square 2 * 2 into 4 squares 1 * 1, are combined. Thus, making a single cut with scissors, we get 4 squares 1 * 1. In fact, a similar problem can be solved for cutting the square n * n into unit squares.
Answer: it is possible.
Task
Find all the rectangles that can be cut into 13 equal squares.
Answer: rectangles with an aspect ratio of 13: 1. The squares into which the rectangle is cut are equal by condition. Therefore, each side of the rectangle is divided into equal parts: one side on m parts and the other on n. The total number of squares is mn, so mn \u003d 13. But the number 13 is prime, so one of the numbers m and n equals 1 and the other equals 13.
Task
Is it possible to cut into four acute-angled triangles a) a convex pentagon, b) a regular pentagon.
hint
B) Each side of the pentagon contains the side of one of the triangles. All angles regular pentagon stupid.
Decision
A) See figure.
B) Each side of the pentagon contains the side of one of the triangles. The pentagon has five sides, and we have four triangles. This means that some two sides of the pentagon contain the sides of the same triangle. Therefore, the angle between these sides is dull. Contradiction to the fact that all triangles must be acute-angled.
Answer: a) Yes; b) no.
Task
Cut one of the figures in the figure into two parts so that each of the remaining ones can be folded. Draw how you cut and how to fold.
Decision
For example, we cut the first shape as shown in Figure 5.2.1. Add the second and third figures as shown in Figure 5.2.2.
Task
Of the two squares, one. There are two squares 3 × 3 and 1 × 1. Cut these squares straight into parts (no more than three), from which one square could be folded.
Decision
In the figure, the problem is solved in the general case. The dotted line indicates the desired square. Prove the equality of triangles numbered by the same numbers.
Task
Is there a quadrangle that can be cut in two straight lines into 6 pieces?
hint
A quadrangle with such a condition must necessarily be non-convex.
Decision
An example is clear from the picture. 
Answer: exists.
Task
Divide the circle with three straight sections into: a) 4 parts; b) 5 parts; c) 6 parts; d) 7 parts.
Answer: for example:
a) or
b) or
c) or
d)
Task
Petya cut the figure into two equal parts, as shown in the figure. Decide how to cut this shape into two equal parts in another way.
Decision
We give two more possible cut options, except for the one given in the condition.
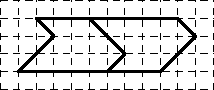
Comment . The figure considered in the problem is an example of an asymmetric figure (which has no center or axis of symmetry), which can be cut into two equal figures in three different ways. It would be interesting to answer the following question: is there an asymmetric figure that can be cut into two equal four or more ways? If you manage to come up with an example of such a figure, please write about this to the jury of the Tournament to them. Lomonosov at [email protected]
Task
The tile has the form of a rectangular triangle with legs 1 dm and 2 dm. Is it possible to add a square out of 20 such tiles?
Decision
Figure 1 shows how this can be done.
Task
Cut the depicted figure into two parts, from which you can fold an entire square 8 × 8.
Answer: See picture.
Task
A dot is drawn inside the circle. Show that you can cut the circle into two parts so that you can make a circle from them, in which the marked point is the center.
hint
The boundary of the cut should be an arc of a circle centered at a drawn point.
Decision
Let O be the center of a given circle S, and A a drawn point. If A coincides with O, then there is nothing to redraw. Otherwise, draw a circle S "with a center in A and a radius equal to the radius of the circle S. This circle will split the circle S into two parts. The first of these parts contains points A and O and is symmetrical about the middle perpendicular m drawn to the segment AO. We leave this part We shift the second part (in the form of a "month") so that it occupies a position symmetrical to its initial position with respect to m. After this, the first and second parts fill the interior of the circle S ". Thus, the required redrawing of the circle is done.
We also give another solution.
We make a cut along a circle passing through points O and A and lying entirely in a given circle. It turns out two pieces: one is a circle, and the other is an asymmetric ring. Now we turn the circle around its center until point A coincides with the center of the circle S - point O.
Task
What is the smallest number of lines that you can cut all the cells of a 3 * 3 chessboard?
hint
One straight line is definitely not enough.
Decision
An example with two straight lines is shown in the picture. On the other hand, one straight line is not enough. In fact, it is easy to understand that one straight line cannot cross even three of the four corner cells.
Answer: two.
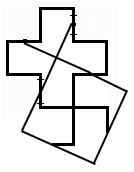
Task
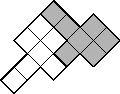
The Snow Queen prefers perfect shapes, which is why she loves squares so much. She gave Kai a cross (see the figure on the right) so that he would divide it into equal parts and assemble a square from them. How can I do that?
Decision
Let the length of each side of the cross be equal to 1. Then it is necessary to cut the cross into parts so that a square of area 5 can be assembled from these parts.
Connect the midpoints of the opposite sides, as in the figure. From the four figures obtained, we add the desired square.
Task
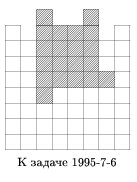
Kai has a piece of a chessboard 7 × 7 cells of precious crystal and a diamond knife. Kai wants, without losing material and making cuts only along the edges of the cells, to cut the board into 6 parts so that they make three new squares, all of different sizes. How to do it?
Decision
From a 7 × 7 square, only squares with sides 2, 3 and 6 can be obtained by cutting, since the number 49 can be expanded into the sum of three squares in only one way: 49 \u003d 36 + 9 + 4. For an example of cutting into six parts, see the figure:
Here you can add a 6 × 6 square from the green parts. There is a way to solve the problem by cutting the square into five parts:
Task
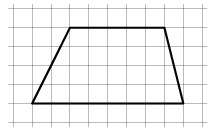
The lengths of the trapezoid bases are m cm and n cm (m and n are natural numbers, m is not equal to n). Prove that the trapezoid can be cut into equal triangles.
Decision
Let m\u003e n. We extend the sides of the trapezoid to the intersection and divide each side of the resulting triangle into m equal parts. Through the points of division we draw straight lines parallel to the sides of the triangle (see Fig. 8.1), and by the Thales theorem we obtain a partition of the triangle into equal small triangles. The upper base of the trapezoid is one of the drawn lines, since its length is expressed by an integer number of centimeters. Thus, we obtained a partition of the trapezoid into equal triangles.
Fig. 8.1
Task
In an isosceles trapezoid, one of the bases is three times larger than the other. The angle with a larger base is 45 o . Show how to cut a trapezoid into three parts and fold a square out of them. Justify the decision.
Decision
Let the foundation ADthis isosceles trapezoid Abcdthree times the base BC, BAD \u003d CDA \u003d45 o . Draw the heights BEand CH. Then
AE \u003d DH \u003d \u003d \u003d BC.
In a right triangle Chdacute angle is 45 o , then this triangle is isosceles. Triangle Bchequals triangle Chdin two legs. From triangles Abh, Bchand Chdcan fold the square Abhk.
Task
Show how to cut any quadrangle into three trapezoids (a parallelogram can also be considered a trapezoid).
Decision
Let B - the largest The inner corner of this quadrilateral is ABCD. Draw a section BM from vertex B parallel to side AD (point M falls inside the quadrangle). From point M, we draw sections MN and MK parallel to the sides BC and CD, respectively (Fig.). 