How to draw a regular pentagon. How to draw a star using a ruler quickly

Correct pentagon Is a geometric figure. It has five angles and equal sides. The image of the pentagon is widely used everywhere - from stationery to huge buildings, for example, the Pentagon, the US Department of Defense. You can draw it without resorting to measuring the sides with a ruler.

You will need

Album sheet, pencil, compass, ruler and eraser.

Instruction manual

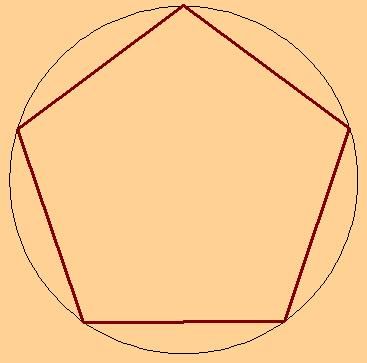
In the middle of the leaf, draw a horizontal centerline. Divide it in half and place the compass leg at the resulting point. Then make a circle of arbitrary diameter. In its middle, a regular pentagon will be drawn.

At the intersection of the circle with the horizontal line, point B, put the leg of the compass and measure the distance to the opposite side. This will be the size of the diameter of the shape. Now draw a semicircle with a radius equal to the diameter of the drawn circle. The edges of the line should go slightly beyond the upper and lower points. In the same way, draw a semicircle on the opposite side. Draw an axial vertical line through the intersection points of the two semicircles above the top and below the bottom points.

Put the leg of the compass at point B. Measure the distance to point O - the intersection of the two center lines. Draw a semicircle with a radius equal to the length of the segment OB. Mark the points of intersection with the border of the circle. Draw a vertical line through them. It will intersect with the horizontal centerline. At the intersection point C, put the leg of the compass and measure the distance to A. Draw a circle with a radius equal to the obtained distance CA.

At the intersection of the circle with the axial horizontal line, put point D. Put the leg of the compass in A and draw a semicircle with a radius AD. The points of intersection with the circle are E and F.

The circle centered at point C intersects with the horizontal axis line at points D and, conditionally, with point M. At point A, put the leg of the compass and draw a semicircle with radius AM. The points of its intersection with the circle, with center O, are denoted by H and G. Thus, points A, F, H, G and E will be the vertices of a regular pentagon. Now connect in straight lines in pairs: AF, FH, HG, GE and EA. The result is a drawn regular pentagon AFHGE.

note

How to build a regular pentagon? Which method is the easiest? The easiest is to take a stencil with a pentagon and circle. Second in simplicity, with a ruler and a protractor. Third, with a ruler, compass and calculator: 1) draw a circle with a radius equal to the side of the pentagon. 2) draw the same circle centered on one of the points of the first circle.

Useful advice

How to build a regular pentagon - in order to build a pentagon you need to have at hand: a sheet of paper, a simple pencil, a ruler, a compass, an eraser .. Now you need to know the size of your pentagon. This will be the center of your pentagon. How to draw a regular pentagon with equal sides. After we learned that the diameter of the circle is twenty centimeters, this information greatly facilitates the task.

Attention, only TODAY!

All interesting

The shape of a five-pointed star has been universally used by man since ancient times. We consider its shape to be beautiful, because we unconsciously distinguish in it the golden ratio, i.e. the beauty of a five-pointed star is mathematically justified. First ...

The task of fitting a polygon into a circle can often lead an adult to a standstill. A child-student needs to explain her decision, so parents go surfing the World Wide Web in search of a solution. Instruction ...

A polygon is called inscribed if all its vertices lie on a circle. You can enter in a circle any regular polygon, including the one with five sides. In classic drawing, this requires some additional ...

The circumference of a circle cannot be accurately measured with a ruler, and therefore dividing it into equal parts is not an easy task, especially if there are an odd number of these parts. The division of the circle into five parts is carried out using a conventional compass or ...

The tasks of constructing the correct geometric figures train spatial perception and logic. There are many very simple tasks of this kind. Their solution comes down to modifying or combining already ...

One of the first ways to build a regular hexagon was described by the ancient Greek scholar Euclid in his famous work "Beginnings". The method proposed by Euclid is not the only possible one. You will need a compass, a ruler, ...

The construction of any regular polygon is based on the principle of inscribing this figure into a circle. The twelve-sided triangle is not an exception, therefore its construction will be impossible without the use of a compass. You will need a compass, ...

A regular polygon is convex polygonwhich has all sides and all angles equal. Around a regular polygon, a circle can be described. It is this circle that helps in its construction. One of the regular polygons, ...

The task of constructing a regular pentagon is reduced to the problem of dividing a circle by five equal parts. Since the regular pentagon is one of the figures containing the proportions of the golden section, it has long been interested in its construction ...

The pentagram, or the five-pointed star enclosed in a circle, has been known since ancient times. Many peoples considered it sacred; it is still used in various rituals. You can draw a pentagram using simple tools. You…

You cannot do without studying the technique of this process. There are several options for doing the job. How to draw a star using a ruler will help to understand the most famous methods of this process.

Varieties of stars

There are many options for the appearance of such a figure as a star.

Ever since ancient times, its five-pointed variety was used to draw pentagrams. This is due to its property, which allows you to make a drawing without tearing the pen from the paper.

There are also six-pointed, eight-pointed tailed comets.

Five peaks traditionally has a starfish. Images of the Christmas version are often found in the same form.

In any case, in order to draw a five-pointed star in stages, it is necessary to resort to the help of special tools, since the freehand image is unlikely to look symmetrical and beautiful.

Drawing execution

To understand how to draw an even star, one should realize the essence of this figure.

The basis for its outline is a broken line, the ends of which converge at the starting point. It forms a regular pentagon - the pentagon.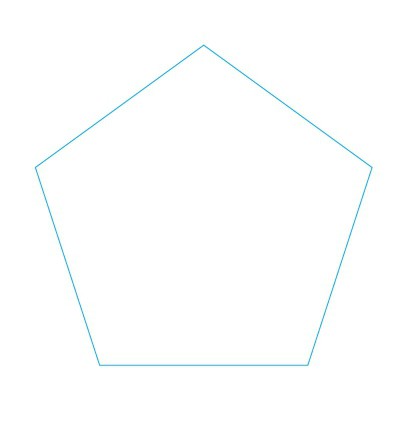

Distinctive properties of such a figure are the possibilities of inscribing it into a circle, as well as circles in this polygon.

All sides of the pentagon are equal to each other. Understanding how to correctly execute the drawing, you can understand the essence of the process of constructing all the figures, as well as various schemes of parts, assemblies.

To achieve such a goal as drawing a star using a ruler, you must have knowledge of the simplest mathematical formulas that are fundamental in geometry. And you also need the ability to count on a calculator. But the most important thing is logical thinking.

The work is not complicated, but it will require accuracy and scrupulousness. The efforts spent will be rewarded with a good symmetrical, and therefore beautiful image of a five-pointed star.

Classic technique

The most famous way to draw a star using a compass, ruler, and protractor is fairly straightforward.

For this technique, you will need several tools: a compass or protractor, a ruler, a simple pencil, an eraser and a sheet of white paper.

To understand how beautifully to draw a star, one should act sequentially, stage by stage.

You can use special calculations in your work.

Figure calculation

Starting to draw a circle should be divided into 5 equal parts. The angle of each will be 72 degrees. Heavily calculated indicators should be applied to the circle manually.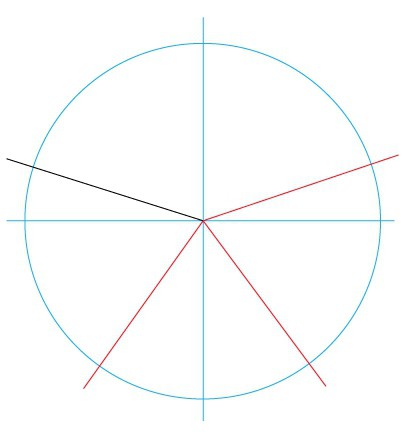

Therefore, it is necessary to build a regular pentagon. To do this, use the system of "golden numbers" of a right triangle with legs 1 and 2, and a hypotenuse equal to the square root of 5.

The solution can be based on calculations of the radius of the main circle or the length of the sides of the pentagon. In the latter version, the upper points of the rays of the star will be located at equal intervals of the vertices of the pentagon.

Arithmetically posed problem is solved inaccurately (there are certain rounding of the results), which is explained by the method of using irrational numbers. Therefore, geometrically drawing a regular, symmetrical star is still easier.

The initial stage of construction

Thinking about how to draw a star using a ruler, you should first draw a circle. It can be performed using a compass, a protractor or an ordinary cup. Having put its upper rim to a sheet of paper, you need to circle its edge with a pencil.

This contour must be drawn very thinly, since it will subsequently be removed with an eraser.

Star building

When drawing a star in stages, it is necessary to divide the circle into 5 equal parts. This can be done using the main rule of geometry.

Measured using a ruler. The resulting value is multiplied by 6.28. The final result will be the distance used to indicate the vertices of the star.

Apply all points evenly on the circle using the calculated value.

To understand how to draw a star in stages, all actions should be performed according to clearly calculated values, not rounding them. Otherwise, the work will turn out to be insufficiently correct and aesthetic.

The vertices marked earlier are connected to each other.

Volumetric shape

To ensure the volume of the figure, it is necessary to draw the main faces. To do this, connect all points of acute angles with the opposite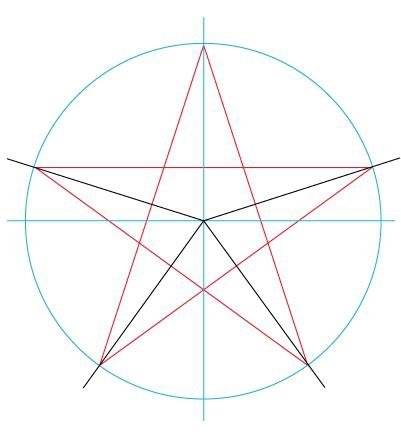

At this stage of drawing the right star, the contours of the finished figure appear.

If everything is done correctly, the resulting image will be smooth. This can be checked visually by rotating a sheet of paper and evaluating the shape. It will be unchanged at every turn.

The main contours are drawn with a ruler and a simple pencil more clearly. All auxiliary lines are retracted.

To understand how to draw a star in stages, all actions should be carried out thoughtfully. In case of an error, you can correct the drawing with an eraser or carry out all the manipulations again.

Work design

The finished form can be decorated in a variety of ways. The main thing - do not be afraid to experiment. Fantasy will tell you an original and beautiful image.

You can decorate a painted smooth star with a simple pencil or use a wide variety of colors and shades.

To figure out how to draw the right star, you need to adhere to perfect lines in everything. Therefore, the most popular design option is to divide each ray of the figure into two equal parts by a line from the top to the center.

You do not have to separate the sides of the star with lines. It is allowed to simply paint over each ray of the figure with a darker shade from one side.

This option will also be the answer to the question of how to draw the right star, because all its lines will be symmetrical.

If desired, with the aesthetic design of the figure, you can add an ornament or other all kinds of elements. By adding circles to the tops, you can get a sheriff star. Applying a smooth shading of the shadow sides, you can get a starfish.

This technique is the most common, because without much effort it allows you to understand how to draw a five-pointed star in stages. Without resorting to complex mathematical calculations, it is possible to obtain the correct, beautiful image.

Having considered all the ways to draw a star using a ruler, you can choose for yourself a more suitable one. The most popular is the geometric stepwise method. It is quite simple and effective. Using fantasy and imagination, you can create an original composition from the resulting correct, beautiful form. There are a lot of design options for the picture. But you can always come up with your own, the most unusual and memorable story. The main thing - do not be afraid to experiment!

Regular polygons in ancient times were considered a symbol of beauty and perfection. This is understandable: because of all the polygons with a given number of sides, the regular polygon is most pleasing to the eye, for which all sides are equal and all angles are equal.

The practical task of constructing such polygons using a compass and a ruler has a long history. Euclid in his work on geometry gives ways to construct a regular triangle, quadrangle (square), pentagon and pentagon, as well as all polygons that are obtained from them by doubling the number of sides (not necessarily single). Consequently, the ancient Greeks could build regular polygons with the number of sides equal to

3, 4, 5, 6, 8, 10, 12, 15, 16, ...

For a long time, mathematicians were especially interested in the question of constructing a regular heptagon. Only in 1796 C. F. Gauss proved the fundamental impossibility of this construction using only the compass and the ruler. Moreover, he proved that among regular polygons with an odd number of sides, only those can be constructed for which the number of sides is either a prime number of the form 2 2 m + 1, m \u003d 0, 1, 2, ... (of which there are currently only five known: 3, 5, 17, 257 and 65 537 ), or the product of several such different numbers. Thus, the list begun above cannot be supplemented with numbers 7, 9, 11, 13, 14, but you can only continue as follows:

17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, ...

(note that regular polygons with too many sides in appearance differ little from an ordinary circle).

In this section, we suggest that you yourself look for ways to build regular polygons inscribed in a given circle or having a given side. No less important practical value have approximate construction methods in those cases when the exact construction by compasses and a ruler is not feasible.

15.1. Inscribed n-gon

Prove that to build a regular n-gon inscribed in a given circle, it is enough to divide this circle into n equal parts and to connect the resulting division points in series with cords. How can one approximately divide a circle into a given number of equal arcs?

15.2. Reduction in the number of parties

A regular polygon is given, the number of sides of which is the product of the natural numbers k and m, where m\u003e 2. How to build a regular m-gon?

15.3. Doubling the number of parties

A regular polygon is inscribed in a circle. Build a regular polygon with twice as many sides as the original.

15.4. Given triangle

Draw a regular triangle with the side equal to the given line.

15.5. Inscribed hexagon

Enter a regular hexagon in this circle.

15.6. Given hexagon

Build a regular hexagon, with the side equal to the given line.

15.7. Inscribed triangle

Enter a regular triangle in this circle.

15.8. Preset square

Build a square with the side equal to the given line.

15.9. Inscribed square

Enter a square in the given circle.

10/15. Inscribed octagon

Enter a regular octagon in this circle.

11/15. Inscribed dodecagon

Enter a regular dodecagon into this circle.

12/15. Inscribed hexagon

Enter a regular hexagon in this circle.

15.13. Given octagon

Draw a regular octagon with the side equal to the given line.

15.14. Preset Twelve

Build a regular dodecagon with the side equal to the given line.

15.15. Hexagon Set

Draw a regular hexagon with a side equal to the given line.

15.16. Golden Section

Divide the segment into two unequal parts so that the square of the largest of them is equal to the product of the length of the entire segment and its smaller part.

15.17. Decagon

Prove that the side of a regular decagon inscribed in a circle is equal to most of the "golden section", the radius of this circle. Enter a regular decagon in this circle.

5.18. Inscribed pentagon

Enter a regular pentagon in the given circle ^

5.19. Star

How to build a five-pointed star?

5.20. Pentagon

Enter a regular pentagon into this circle.

5.21. Given pentagon

Build a regular pentagon with the side equal to the given line.

15.22. Approximate construction of the heptagon

Draw a circle and write a regular triangle into it. Then, starting from one of its vertices, successively make six serifs on the circumference with a compass solution equal to half the side of the triangle, and construct a heptagon with vertices at the six points obtained and at the starting point.

How accurate is the proposed method for constructing a regular heptagon?

15.23. Approximate construction of a quadrangle

Draw a circle of large radius G with the center at point O (Fig. 47), which we divide into six equal parts by points A 1, A 2, A 3, A 4, A 5, A 6. With centers at points A 2, A 4 and A 6 draw arcs of circles of the same radius, forming a figure of three "petals". Radius A 1 O divide into three parts and through the division point closest to the point О draw a line perpendicular to this radius. A segment of its BC contained inside the petal will be taken as the side of the decagon inscribed in the circle of radius OB.

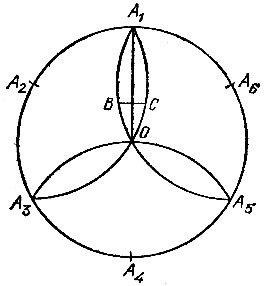
How accurate is the proposed method for constructing a regular hexagon?

15.24. Approximate construction of an n-gon

On the diameter AB of a given circle, as on the side, we construct a regular ACB triangle (Fig. 48). We take the point D on the segment AB so that the equality

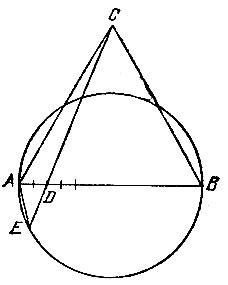
We continue the segment CD until it intersects about a circle at point E. We take Aordu AE as the side of the n-gon inscribed in this circle.

How accurate is the proposed method for constructing a regular n-gon?

Solutions

15.1. If all I sides of the inscribed self-gon are pulled together by equal arcs of a circle, then the sides themselves are equal. In addition, in this case, each of the angles between the adjacent sides of the n-gon is inscribed and relies on an arc made up of n-2 mentioned identical arcs. Therefore, all these angles are also equal to each other. Thus, the problem of constructing an inscribed regular n-gon is reduced to dividing the circle by i equal fools.

If you have a protractor at hand, then with its help 360 ° you can draw a central angle equal to. Putting aside one such angle from some radius OA 1, we get the radius OA 2. Setting aside another similar angle from it, we obtain the following radius OA 3, etc. Points A 1, A 2, ..., A n will divide the circle into n parts, and to what extent these parts will be equal, will depend on the accuracy with which the required central angles were laid.

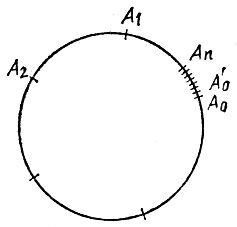
In the absence of a protractor, you can apply the following method of approximating the division of a circle into a given number n of equal parts using a compass. We choose a solution of the compass by eye so that it approximately corresponds to the distance between the adjacent vertices of the future n-gon, and set aside from any point A 6 on the circle n of the solutions of the compass in a certain direction, obtaining successively the points A 1, A 2, ..., A n. If the points A 0 and A n practically coincide, then the solution of the compass is already selected by us quite accurately. If these points somehow noticeably differ, then we divide the arc A 0 A n into n approximately equal parts and mark the division point A 0, which is closest to the point A 0 (Fig. 49). Adjust the compass solution so that it corresponds to the distance between points A "0 and A" 1, and repeat all over again, setting aside n solutions of compass from point A "0 and obtain points A "1, A" 2, ..., A "n. By comparing the points A "0 and A" n, we again find out whether the compass solution turned out to be sufficiently accurate. If not yet, we’ll fix it again, etc., until the desired accuracy is achieved.

15.2. Let be A 1, A 2, ..., A km - consecutive vertices of the original polygon. Then a polygon with vertices A 1, A 2, ..., A km will be correct, because these vertices lie on the same circle (described near the original polygon) and divide it into equal arcs.

15.3. Draw a middle perpendicular to each side of this polygon until it intersects about an arc of a circle contracted by this side. Since the obtained intersection points divide each of the arcs into two equal parts, these points together with the vertices of the original polygon form the vertices of the desired polygon.

15.4. Let AB be a given segment. We draw two arcs of circles with centers at points A and B and radius AB until they intersect at point C. Connecting points A and B with point C, we obtain the required regular triangle ABC.

15.5. We take an arbitrary point A on this circle with center O and a compass solution equal to OA, put five more points B, C, D, E and F on the circle in succession. Points A, B, C, D, E and F are vertices of a regular hexagon . In fact, connecting these points in series with each other and with point O, we get five equilateral triangles (Fig. 50). Since each of the angles AOB, BOC, COD, DOE, EOF is equal to 60 °, the angle AOF is also equal to 60 °, which means that the circle is divided into six equal arcs.

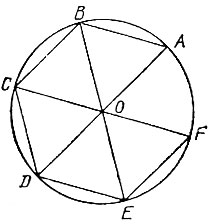
15.6. With a solution of the compass equal to the length of this segment, draw a circle. Inscribing the hexagon into this circle by the method proposed in solving Problem 15.5, we obtain a regular hexagon with a given side.

15.7. Divide this circle into six equal parts (see Problem 15.5) and divide points through one in series with chords. We obtain a regular triangle (see problem 15.2).

15.8. From the ends of this segment AB, we restore the perpendiculars AM and BN on one side of the segment AB (Fig. 51) and set aside the segments AD and BC equal to the segment AB, Connecting points C and D, we get the square ADCB. In fact, the quadrilateral ADCB is a parallelogram (for its sides AD and BC are equal and parallel), a rhombus (for AB \u003d BC) and a rectangle (for ∠ ABC \u003d 90 °), which means a square.

15.9. Through the center of the circle we draw two mutually perpendicular diameters AC and BD and connect their ends in series with the chords. We get the inscribed square ABCD. Indeed, the arcs AB, BC, CD and AD are equal to each other, since they are based on equal central angles of 90 ° each.

15.10. We write a square in the given circle (see problem 15.9) and double the number of its sides (see problem 15.3).

15.11. Doubling the number of sides of a regular hexagon inscribed in a given circle, we get a regular twelveagon inscribed in the same circle (see problems 15.5 and 15.3).

15.12. Doubling the number of sides of a regular octagon inscribed in a given circle, we get a regular hexagon inscribed in the same circle (see problems 15.10 and 15.3).

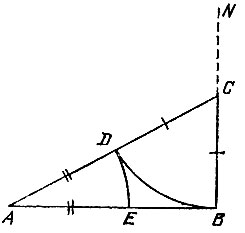
15.13. From the middle C of this segment AB (Fig. 52), we restore the perpendicular and set aside the segment CD equal to 1/2 AB. Then, on its continuation, we postpone the segment DO equal to AD. Then the segment AO is the radius of the circle described near the regular octagon with side AB.

In fact, we find the magnitude of the angle AOS. Because AC \u003d CD, then the triangle ACD is isosceles, and since it is rectangular, the angle ADC is 45 °. Because the AD \u003d DO, then the triangle ADO is isosceles and the angle AOD is equal, and therefore, the angle AOB is 45 °, that is, the arc AB is 1/8 of the circle.

Now, on a circle of radius AO from any point, we sequentially defer seven arcs, each of which is equal to the arc AB. Get the vertices of a regular octagon.

15.14. We construct an equilateral triangle of the ACB with a side equal to this segment AB. Through point C we draw a line perpendicular to the segment AB. Put on this straight line the segment of SB equal to AB (Fig. 53). Then the segment AO is the radius of the circle described near a regular dodecagon with side AB. To confirm this, it is enough to prove that the angle of AOB is 30 °. Point C is equidistant from points A, B, and O, i.e., it is the center of the circle circumscribed near the triangle AOW. therefore

Now, on a circle of radius AO from any point, we successively postpone 11 arcs, each of which is equal to the arc AB. We get the vertices of a regular dodecagon.

15.15. From the middle C of segment AB, we restore the perpendicular (Fig. 54) and on it we set aside segment CD9 equal to 1/2 AV, then segment DE equal to AD and segment BO equal to AE. Then the segment AO is the radius of the circle described near a regular hexagon with side AB.

As in problem 15.13, we find that

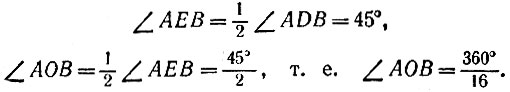
The construction of a regular hexagon is similar to the construction in previous problems.

Now, on a circle of radius AO from any point, sequentially lay 15 arcs, each of which is equal to the arc AB. We get the vertices of a regular hexagon.

15.16. Let a given segment AB be of length a. Find the length x of most of the "golden section" of segment AB. Out of proportion

we get

Therefore, the problem reduces to constructing a segment of a specified length x from a segment of length a. Number equal to the length of the hypotenuse of a right triangle with legs a and a / 2, which can be built using a compass and a ruler. To get a length it is enough to subtract a segment of length a / 2 from the hypotenuse of the constructed triangle. Therefore, the construction of the "golden section" of the segment AB can be done as follows (Fig. 55):

from point B we restore the perpendicular BN to the segment AB, on it we postpone the segment BC of length 1/2 AB;
we connect the points A and C and set aside the segment DC of the BC length on the AC segment;
set segment AE of length AD on segment AB, then point E divides segment AB in the "golden section".

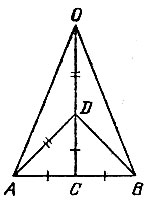
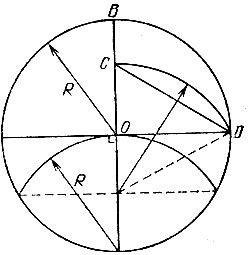
15.17. Let AB be the side of a regular decagon inscribed in a circle. Then ∠ AOW \u003d 36 °, and each of the angles of OAV and ABO is equal to 72 ° (Fig. 56). We draw a bisector AC of angle A of triangle AOW. Because ∠ ASB \u003d 72 °, then from isosceles triangles ABC and ASO we get AB \u003d AC \u003d OS.

By the property of the bisector of the triangle, we have OS: BC \u003d AO: AB. Because the AO \u003d OB, AB \u003d OS, then OS: VS \u003d OV: OS, i.e. OS 2 \u003d BC * OV, and this means that the radius of the organic matter is divided by point C in the "golden section", and the OS is a large part of the radius (because ∠ ACB\u003e ∠BAC, where from OS \u003d AB\u003e BC).

Thus, dividing the radius of the OB of this circle in the “golden section” (see Problem 15.16) and taking most of the OS, we will find the length of side A B of the regular decagon inscribed in this circle. Now, from any point of the given circle, we sequentially lay nine chords, each of which is equal to AB. One specific way to build a party OS \u003d AB the required decagon is shown in Fig. 57.

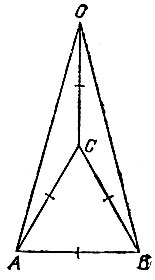
15.18. Divide this circle into 10 equal parts (see problem 15.7). Then the division points taken through one are the vertices of a regular pentagon (see problem 15.2). However, in fig. 57, where the segment of the OS is built, equal to side of a regular inscribed decagon, there is also a segment CD equal to the side of the required pentagon.

15.19. We draw a circle, divide it into 5 equal parts (see Problem 15.18) and connect the division points through one chord with each other, as indicated in Fig. 58.

15.20. Because the 1 / 6 - 1 / 10 = 1 / 15 , then, taking away from the arc equal to 1/6 of the circle, the arc equal to 1/10 of the circle, we get the remainder equal to 1/15 of the circle. This observation allows us to inscribe a regular pentagon into the circle (methods for dividing the circle into 6 and 10 parts are described in problems 15.5 and 15.17).

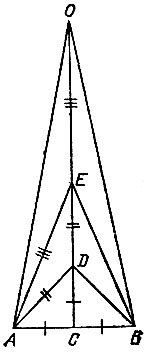
15.21. From the end A and middle C of the given segment AB, we reconstruct the perpendiculars AN and CM and draw a circle with center A and radius AB (Fig. 59). On the perpendicular AN, set aside the segment AD of the length AC and draw the segment BD. We set aside the segment DE of length AD on the segment BD and draw a circle with center B and radius BE until it intersects the first circle at point F. On the line AF, construct a point G at a distance AB from point B. Then, the center О of the circle circumscribed about a regular pentagon with side AB, lies at the intersection of the straight line CM with the middle perpendicular to the segment BG. Indeed, the circle circumscribed around the triangle ABG is also circumscribed around the required pentagon, since the inscribed angle BAG is equal to the central angle BAF, which rests on the side FB of the decagon inscribed in the first circle (see Problem 15.17), and therefore equal to 36 ° . Therefore, the angles of BOG and AOB are 72 ° each. The remaining two vertices of the pentagon lie at the intersections of the circumscribed circle with the perpendicular CM and with the first circle, respectively.

and therefore, as a result of six laying off of the arc AE on the circle, the construction error, although it will accumulate, will not exceed 6 (β - α). Thus, the described method allows you to build a "practically regular" heptagon.

15.23. Let the D-point of intersection of the segments BC and OA 1, E be the middle of the segment OA 1, and CF be the perpendicular to the line A 1 E (Fig. 61). Then if OA 1 \u003d R, then and from right triangles A 2 OE and A 2 CF we have

where do we get

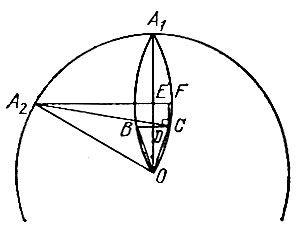
According to the tables of tangents we find

therefore, the central angle BOC, which should be 40 ° for the regular heptagon, in our case differs from the desired value by no more than 25 ". Moreover, the error at the other angles also does not exceed 25": the other two “petals” give the same angles, and the angles between the "petals" are simply divided in half, which makes the error only halves. Thus, the resulting hexagon is "practically correct."

A graphic star is a five-pointed figure that is difficult to draw by hand. In order for the star to be neat with proportional even rays, it is better to depict it using drawing tools - a ruler, protractor, compass.

How to draw a star with a ruler and pencil

The five-pointed star consists of five faces, which are formed by connecting straight segments at a certain point. There is a way in which, by calculating and connecting the points in the desired order, you get a star. For work, take: a sheet of paper, a pencil, an eraser, a calculator.

Set your desired star length. Suppose this is 12 cm, designate it as X.

On a sheet of paper, draw two parallel beams, the distance between which is - 12: 1.55 \u003d 7.7 cm.

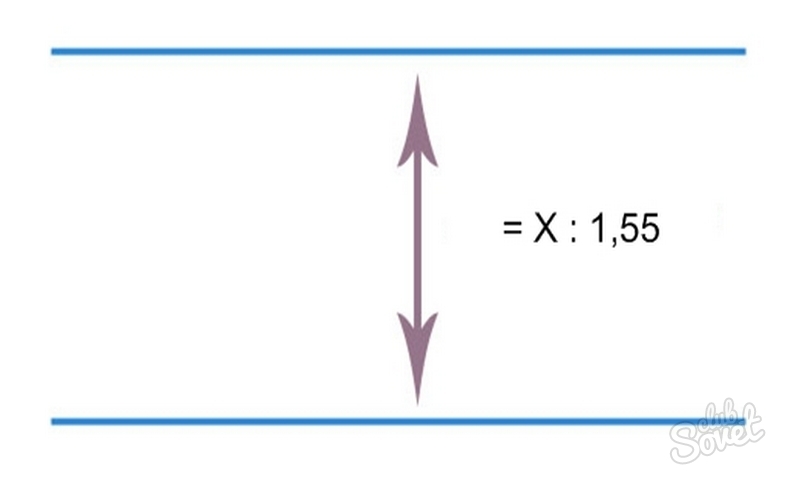
Draw a perpendicular running through the middle of the line segments. On the first line of the figure, from the center to the edges, lay down the same segments calculated by the formula: X: 2 \u003d 12: 2 \u003d 6 cm. Put points on their ends.

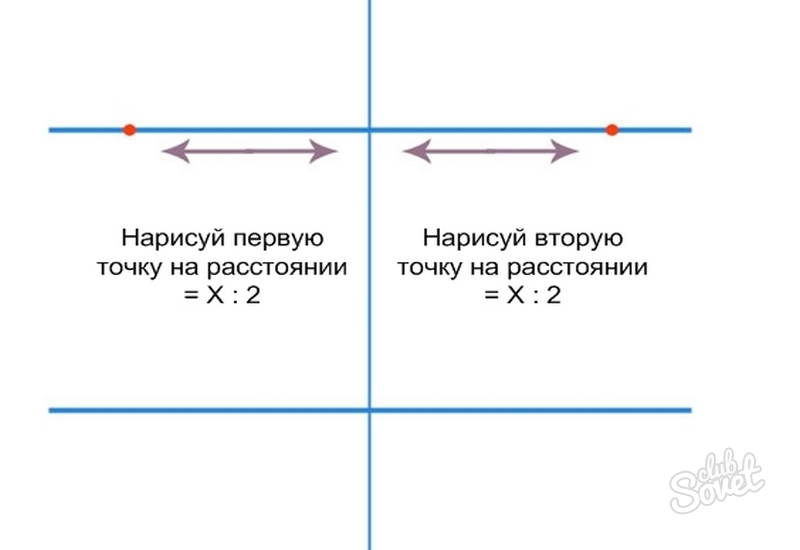
On the bottom line, do the same, only calculate the length of the parts as follows: X: 3 \u003d 12: 3 \u003d 4 cm.

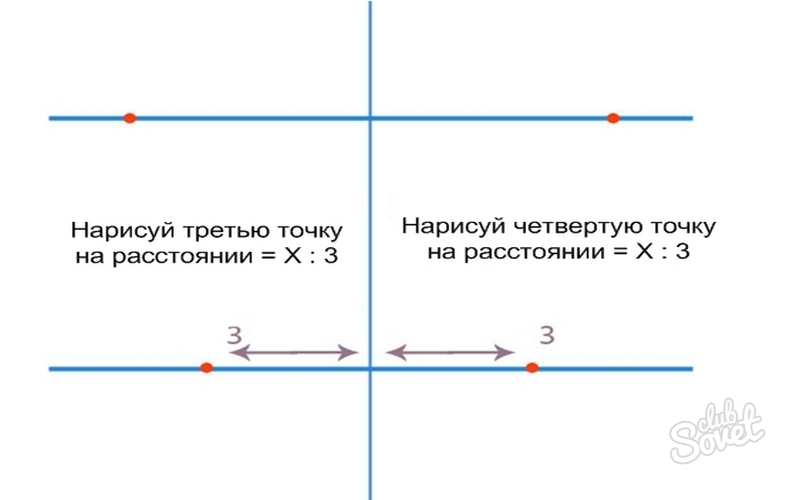
On the middle line, measure up: X: 2.6 \u003d 12: 2.6 \u003d 4.6 cm.

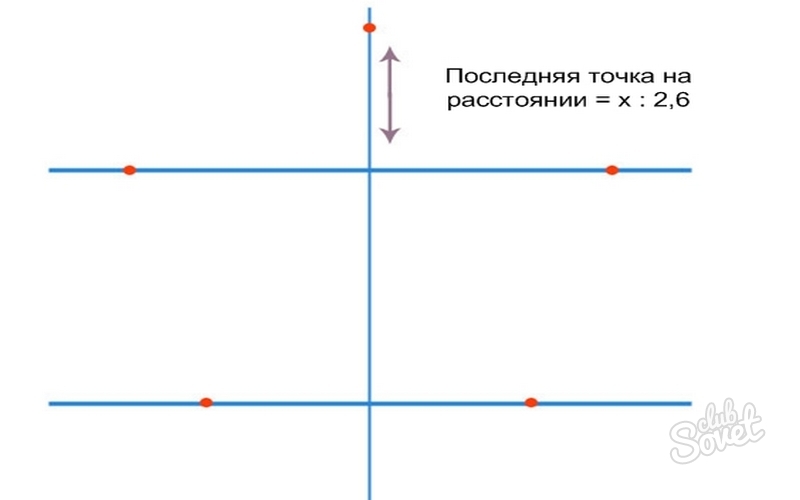
Draw lines on the dots and the star is ready.

How to draw a star using a ruler and compass

In this option, you will need not only a pencil, a ruler, but also a compass.

Draw a circle on the sheet. Break it into 4 parts by drawing perpendicular diameters, then divide the quarters in half.

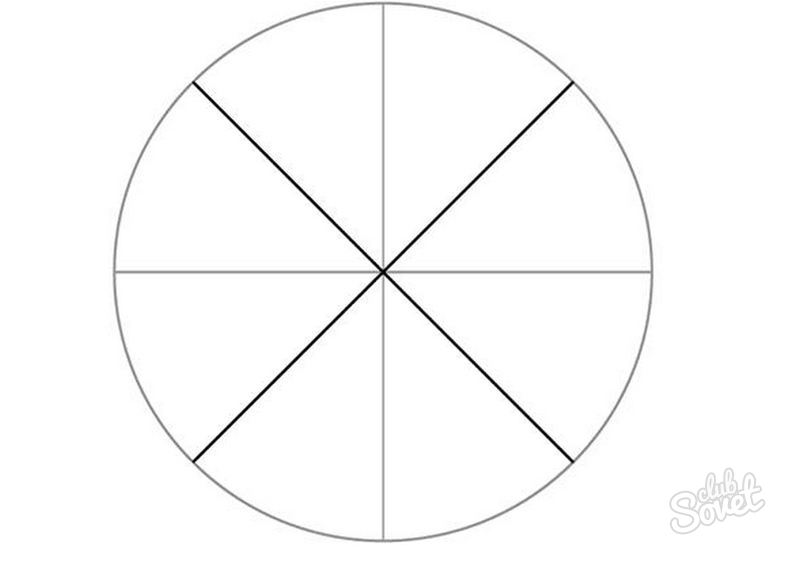
Split the resulting sections into two parts. In the lower segments (see the figure), put the dashes in the middle of the second from the perpendicular eights.

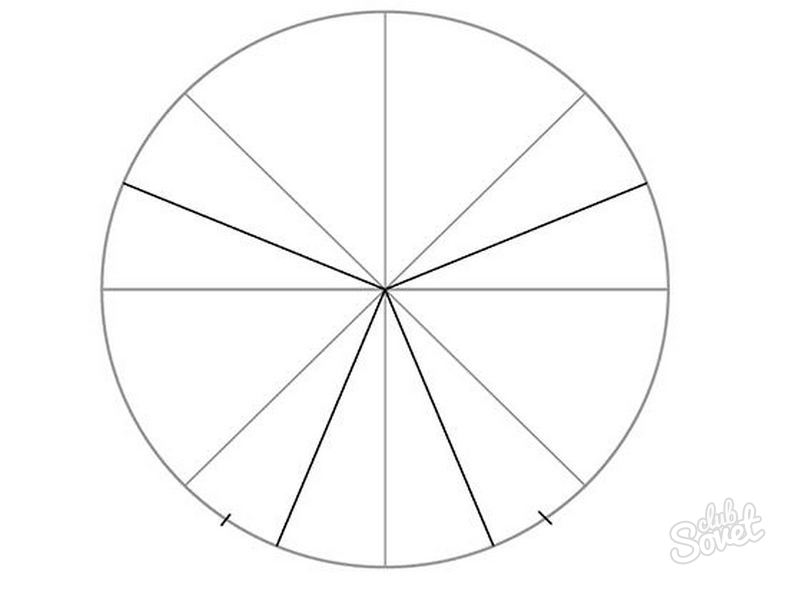
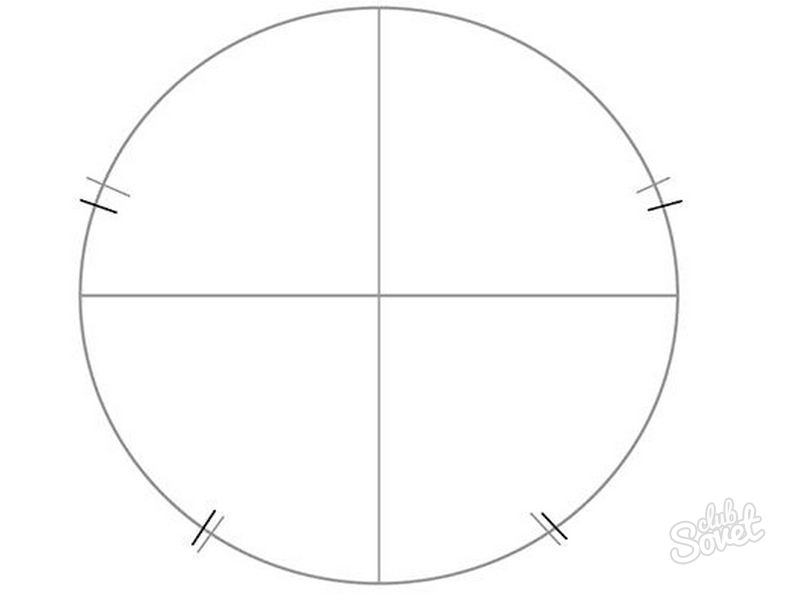
Remove the mark, leaving the guidelines as in the diagram.

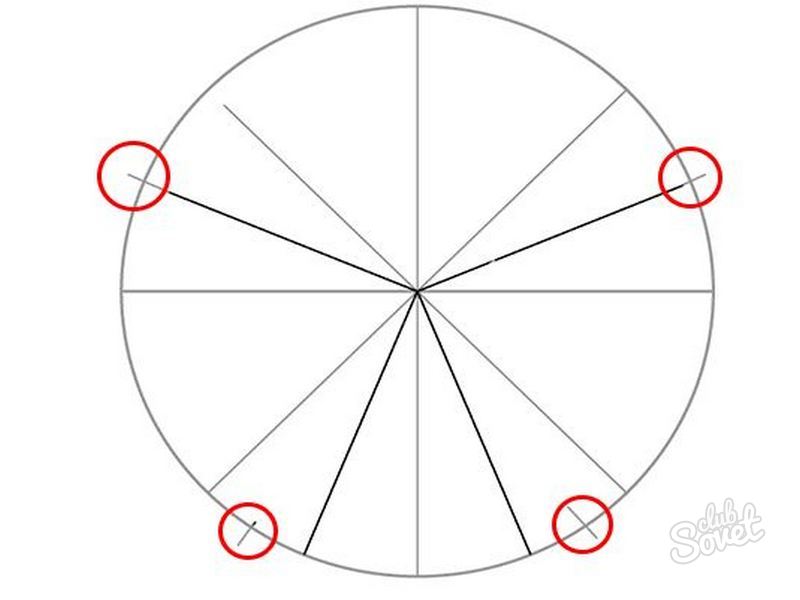
Double the dashes in the sectors, the distance between which is 1 cm in the upper segments and 0.5 cm in the lower segments.

Connect the lines of the star grid over the red dots.

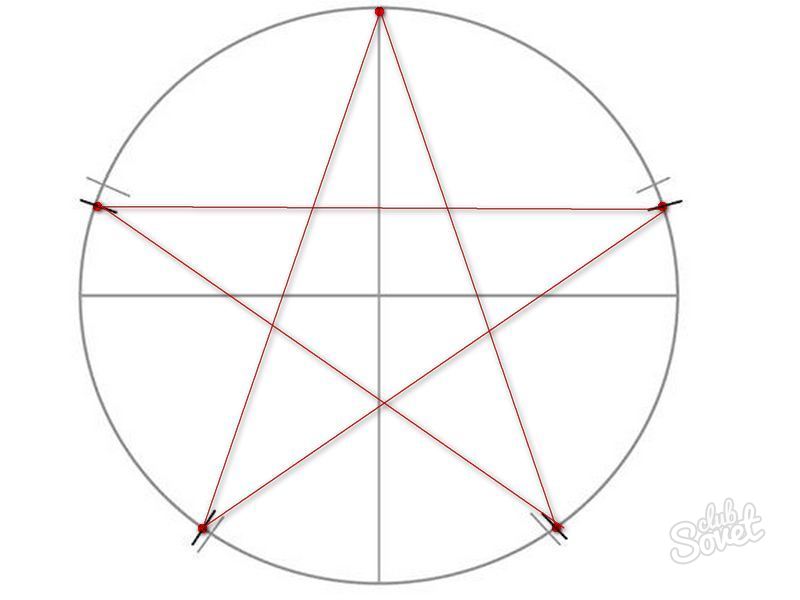
Erase the circle, add a picture of the volume, drawing segments from the middle of the star to all its corners.

Paint the star with scarlet color, circling the edges and contour with a contrasting felt-tip pen, cut out the figure and decorate the home-made greeting card for February 23 or Victory Day.

How to draw a star using a ruler and protractor

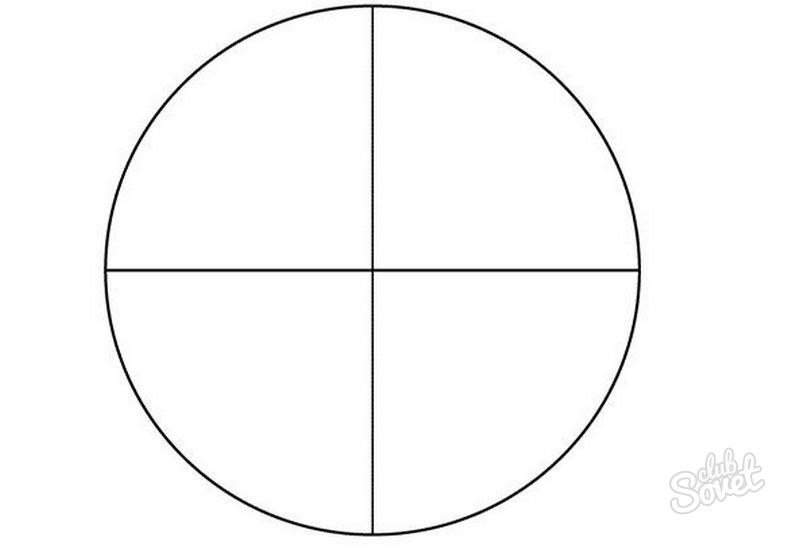
Prepare paper, pencil, ruler, compass, protractor.

Mark a circle on paper and divide it into slightly visible rays into 4 parts.

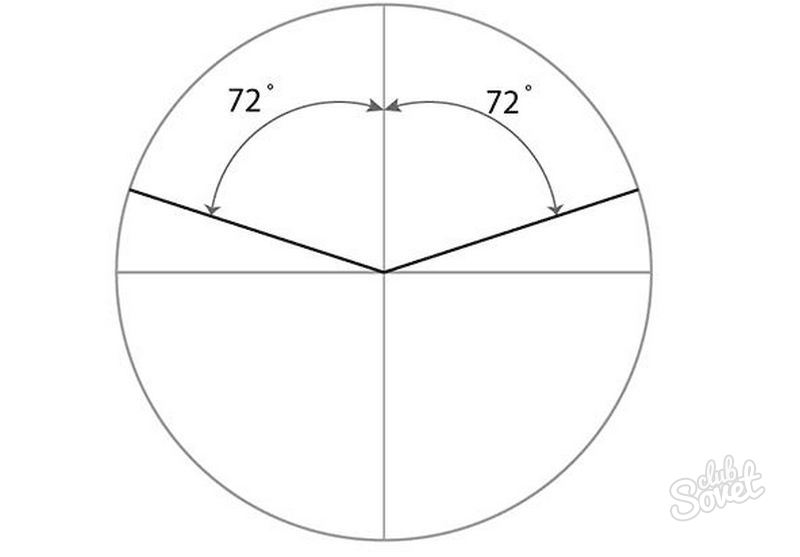
Place the protractor at the top of the circle in vertical diameter. Measure it to the right and left at 72º and draw rays from the center of the circle to its arcs.

From the left ray again take 72º, and so on until the end, until the circle is divided into 5 parts.

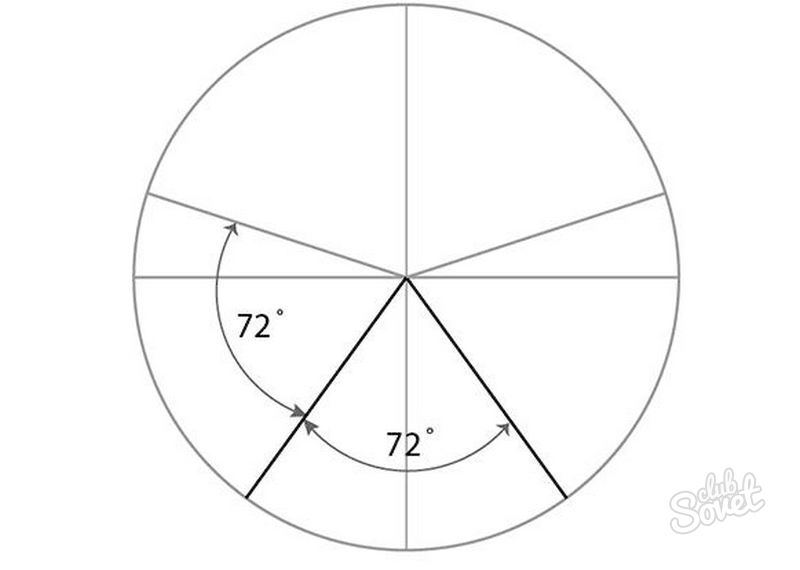
Close the lines according to the pattern.

Erase all unnecessary outlines. All - the work is done. Now put your knowledge into practice - make a colorful application of the night sky or a festive salute.

How to draw a star using a ruler and inscribed pentagon

It is easy to draw a star by inscribing a pentagon into a circle.

Make a circle, split it in two twice, then divide the arc of a circle into the eye into 5 equal parts. Connect the intersections of the faces with segments and get a regular pentagon.

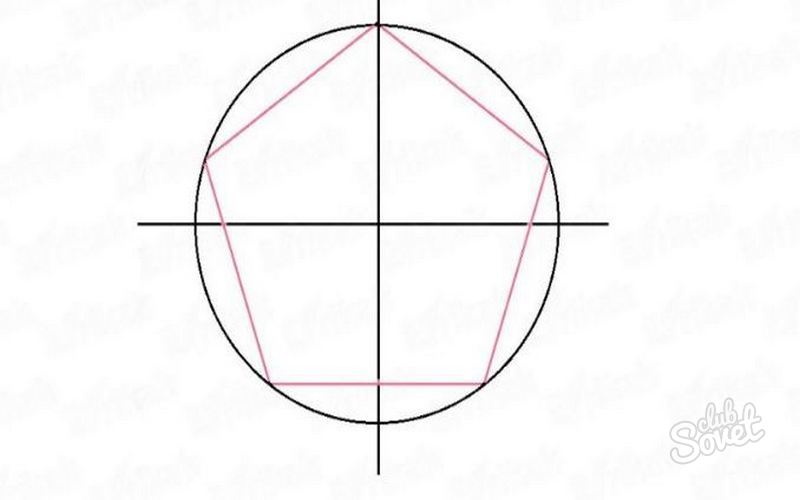
Build a triangle starting from a vertical line.

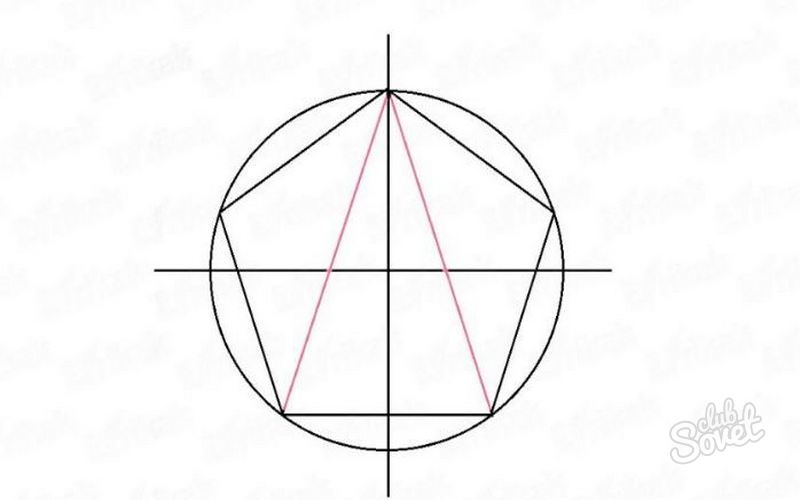
From the upper corners of the figure, draw segments to the lower corners. Draw a diagonal parallel to the basting diameter and connect the opposite corners.