Constructing a circle center with a compass. The results of the study of students in the project study the regular polygons

Topic: Circle, circle. Compass. Center, radius. Building a circle with a compass.

Goal:

Educational: To form initial ideas about a circle and its elements (center and radius);

introduce a new drawing instrument - a compass and safety rules for handling a piercing object; to promote the development of attention, thinking, cognitive activity of students, their interest in the subject, the ability to build a circle and radius using a compass and a ruler;

Developing: to develop a cognitive interest in the subject being studied, the ability to analyze, compare and draw conclusions based on reasoning; to enrich the vocabulary of students, to form the ability to make sentences based on supporting words;

Educational: increase cognitive activity, educational motivation, contribute to the development of a harmonious personality; learn to work in pairs, respect the opinions of comrades.

Corrective - developing : to correct and develop cognitive activity of students through the use of perception exercises.

During the classes.

I. Org. moment (Emotional mood through the use of a poem.)

- Let's check if everyone is ready for the lesson?

Smile like the sun.

Frown like clouds.

Cry like rain.

Surprise as if you saw a rainbow.

II. Checking homework.

View pictures. What are the seasons that are depicted on them.

For each season, select the appropriate months. (Autumn - September, October, November. Winter - December, January, February. Spring - March, April, May. Summer - June, July, August).

Retrieve the month names in order.

III. Verbal counting.

Name the round tens.

Count from 56 to 61, from 28 to 38, from 89 to 100.

46 over 72

34 less than 83

Among 89 - 9 dess.

Among 100 - 10 dess.

What geometric shapes are the objects in the pictures.

IV. Post lesson topics.

1 . - You have little leaves on your desks, take a pencil and draw a circle.

Did you get an even circle?

How can I draw an even circle?

Where in life can we meet a circle?

What do you think we will learn in the lesson?

We will learn to build a circle using compasses.

But first, consider what a circle is and what a circle is.

Two brothers came to visit us. (On a magnetic board)

Circle and circle
We live together with my brother, we are so much fun together
We put a mug on the sheet, circle it with a pencil.
It turned out what you need - called the circle.
My brother in painting considers himself a master,
Everything inside the circle, he painted over with a felt-tip pen.
Here is a red circle, a circle, a blue rim around the edge.

The boundary of a circle is a circle.

The circle has one girlfriend

Everyone knows her appearance!

She walks around the edge of the circle

And called - circle!

2. Work in notebooks.

- Record today's number. Classwork.

Now pick up the template that is on your desk and, placing it on the notebook sheet, circle with a blue pencil. Remove the template. What is the name of the line of blue color in your notebooks?

Guys, now pick up a red pencil and paint over everything inside the blue line in your notebooks. What figure did you get?

3. The construction of a circle using a compass.

a) - And now we will learn to build a circle using a compass.

Before you start working with the compass, remember the structure of the compass and the rules safety. The compass consists of two legs, at the end of one needle, and at the end of the other - lead. By the head we hold and turn the pair of compasses.

b) -Take the compass and the ruler, apply the compass needle to 0, and move the other compass leg 2cm.

Now move the compass to the notebook. Try to keep the sharp end of the compass in one place and not move. Build a circle.

c) - where the needle of the compass was standing, put a point. This is the center of the circle.

Now put a point anywhere in the circle and connect the center to the point of the circle using a ruler.

A line is the radius of a circle.

Practical work.

Now repeat this work. Put another point anywhere on the circle. Connect it to the center.

What did you get?

· Children answer: we got another radius.

Circle to center

We will draw a long mustache

Every third grader knows

That's for sure - radius!

V. Physical education.

VI. Fastening. Work on the textbook.

- Open the tutorial on page 109, read the rule.

Perform control 2 p. 109

Perform control 5 p. 110

The game "Circle or Circle."

(Children clap if it's a circle, show the ring with their hands, if it's a circle.) Show pictures.

Reflection of activity (lesson summary).

Today in the lesson we met with a geometric figure ...

The boundary of the circle ...

The circle can be drawn with ...

If you succeeded in the lesson, show green circle if you still have unresolved problems - a yellow circle, if you still need help - a red circle

Homework. Learn the rule p. 109

How to find the center of a circle without any tools?
Easy! All you need is a pencil, scissors and a piece of paper. Do not even need a ruler!
   If the circle is already ready, and the sheet of paper has even edges, then you can do without scissors with one pencil, but for clarity, we will cut out the circle and we will have paper with an uneven edge, so we will use scissors.
So, given: a circle that was drawn not in a circular pattern (the center is marked with a needle there right away), but by drawing a pencil around a round object, such as a plate, saucer, cup, or some kind of cover from dishes, packaging, etc.

   Take the first thing that came to hand - a stand from a flower pot standing next to a computer. There is, however, a hole in the center and you can immediately, taking a needle or carnation, mark the center. But we will not look for easy ways and will ignore such an opportunity.
   We draw a circle on a green sheet of paper (I took the cover from the notebook especially for contrast), circle our stand with a pencil.

Cut the circle along the drawn line. It is on it that you need to find a center.

We take a sheet of paper, (any one is suitable, the main thing is to be suitable in size). In this case, a notebook leaflet is quite enough. If the circle is large, then you can take, for example, a large format newspaper. The principle is still the same: we will need square sheet of paper, i.e.., its sides should be all equal to each other.
A sheet of notebook, like a standard sheet of writing paper, have a rectangular shape, not a square shape (newspaper sheet - similarly).

How to make it square? - Bend from corner to corner as shown in the photo.

Anyone who has ever made a paper airplane or some other paper toy at least once in his life has a good idea of \u200b\u200bhow this is done.

The photo shows that the sheet from the notebook was torn out inaccurately, so we bend so that the torn edges are not involved and after bending the sheet we cut them with scissors. We bend the excess of the “rectangle” on the opposite side of the sheet and smooth the folds so that they are clearly visible when the fox is straightened again.

This fold line will tell us the diameter of the circle when we apply it so that the edges touch two sides of the square. At the edges of the circle make marks with a pencil.

Using the folded side of the sheet as a ruler (we agreed at the very beginning that we can do without it) we draw a line connecting these marks.

We turn the circle and in a similar way we outline the points for another diameter.

The intersection of these lines will be the center of the circle. In order to verify this, we can rotate our circle several more times, each time applying its edge to the sides of the square and drawing lines through the marks made opposite the fold line of the square.

All of them intersect in the center of the circle, if you do the work slowly and accurately.
This principle can be used in the home workshop when it is required to determine the center of a wooden blank. And for this it’s easy to do, which will greatly facilitate the markup.

There is a very simple way to find the center of a flat round billet.

All you need to do is circle it around the perimeter, putting it on a piece of paper, then cut a circle along the drawn line, bend it four times and the center will be found. It is located exactly at the intersection line of the folds.
It remains to expand the leaflet, put it on the workpiece so that the edges coincide in the center, make a note with a sharp object, for example, an awl.

And students in grade 9, group "Theorists"

Group research topic

The study of the basic theoretical material necessary for solving problems on the topic "Regular polygons",

as well as in problems of constructing regular polygons.

Study objectives

Answer the questions:

1) What do we know about regular polygons?

2) What formulas are needed when solving problems of finding the elements of the right

polygon and its area?

3) How to build a regular polygon?

Research results

Definition:

Correct is called convex polygonwhich has all angles and all sides equal.

Basic formulas:

1. Side of a regular polygon a \u003d 2R sin 180 / n

2. The radius of the inscribed circle r \u003d R cos 180 / n

3. The area of \u200b\u200bthe regular polygon S \u003d 1/2 Pr

The geometric tasks of building with the help of a compass and a ruler originated in ancient Greece at the time of Euclid and Plato. Even in those days, mathematicians were able to build regular triangles, pentagons and squares using the compass and ruler. Moreover, they knew how to use a compass and a ruler to divide an angle in half, so they knew how to build regular 6, 10 and 15 angles and all regular n-angles. It is very important that using a ruler, only line segments are drawn, and the lengths of the segments are measured using a compass, not divisions on the ruler. So, using these tools you can build a segment whose length is expressed by a number obtained from 1 using four arithmetic operations (addition, subtraction, multiplication, division) and extraction of the square root. Those. in the beginning there is only a segment whose length is taken as 1. Then we can construct a segment whose length is equal to a rational number or the square root of a rational number. Further, if a segment of length a is already constructed using a compass and a ruler, then using these tools you can build a segment of length b if b is expressed in terms of a using arithmetic and the square root. It is said that such a number is expressed in square radicals. Thus, using a compass and a ruler, you can build a segment whose length is expressed in square radicals. The mathematicians of ancient Greece knew all this. The task of constructing other regular polygons (or proof of the impossibility of such constructions) could not be solved for the next two millennia, and it was solved by a German student of the philological faculty of the University of Gottingen, Karl Friedrich Gauss in 1796. At that time, Gauss was 18 years old and he was torn between classes in philology and mathematics and could not make a final choice. Solving an ancient problem helped him make the final choice in favor (and in favor) of mathematics. It’s scary even to think how much the development of mathematics would be slowed down, had Gauss remained a philologist! Until now, mathematicians around the world call Gauss the king of mathematics.

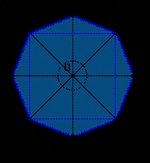
Division of a circle into four, eight equal parts. Building a regular quadrangle and octagon.

Dash-dotted center lines drawn perpendicular to one another divide the circle into four equal parts. Consistently connecting their ends, we obtain a regular quadrangle (Fig. 64).

In order to divide the circle into eight equal parts, it is necessary to divide into two equal parts an arc equal to 1/4 of the circle. Thus, we obtain an arc equal to 1/8 of the circle (A4 \u003d A3). With a solution of the compass equal to A3 or A4, we make serifs on the circle, dividing it into eight equal parts. Consistently connecting the serifs with line segments, we get a regular octagon (Fig. 64).

Build a regular hexagon, the side of which is equal to this segment.

To solve the problem, we use the formula a \u003d P. Let PC be a given segment. We construct a circle of radius PC and mark on it an arbitrary point A1. Then, without changing the compass solution, we construct points A2, A3, A4 ..... A6 on this circle so that the equalities - A1A2 \u003d A3A4 \u003d A5A6 are fulfilled. Connecting the given points in series by segments, we obtain the desired regular hexagon A1A2A3A4A5A6.

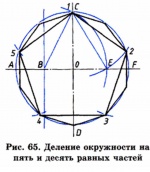
Division of a circle into five and ten equal parts. Building regular pentagon and decagon.

To divide the circle into five equal parts, we find the middle of the radius of the circle OA. Taking point B as the center, draw an arc whose radius is equal to the length of the segment BC until it intersects with the horizontal diameter at point E. The segment CE is the side of the pentagon. The segment OE corresponds to the side of a regular inscribed decagon. Having set aside a value equal to 1/5 and 1/10 of the circle, we divide it into five and ten equal parts. Connecting serifs (vertices of the n-gon) in succession by line segments, we obtain regular penta- and decagons (Fig. 65).

Division of a circle into three, six, twelve equal parts. Building regular polygons.

The division of the circle into three equal parts is as follows. Point C (Fig. 66) is taken as the center from which the arc is drawn, the radius of which is equal to the radius of the circle. The drawn arc will intersect the circle at points 2 and 3. Arcs 1-2, 1-3, 2-3 are the third part of the circle. Connecting the points 1, 2 and 3, we get a regular triangle.

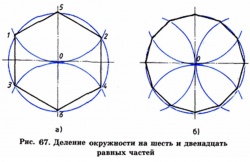
To divide a circle into six equal parts, from any of its points, we set aside segments equal to the radius of the circle (R). The resulting arcs divide the circle into six equal parts. Having taken points 1, 2, 3, 4, 5, 6 as the vertices of the hexagon, we connect them by line segments, as shown in Fig. 67, a. Thus, we construct a regular hexagon.

The division of the circle into twelve equal parts is based on the postponement of segments equal to half the radius of the circle (R / 2) from any of its points. The resulting arcs will divide the circle into twelve equal parts. Taking each serif at the top of the dodecagon and connecting them in series, we get the correct dodecagon and the definition of the radius (Fig. 67, b).

Finding the center of the arc and determining the radius.

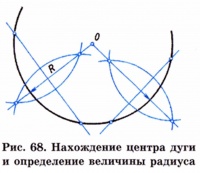
In the practice of carrying out the drawings, it may be necessary to find the center of the arc and determine the value of its radius. To do this, hold two non-parallel chords and restore the perpendiculars to their midpoints. The intersection point of the perpendiculars (point O) is the center of the arc (Fig. 68). From the center measure the value of the radius of the arc.

If some regular n-gon is constructed, then with the help of a compass and a ruler it is possible to construct a regular 2n-gon. Let us describe near this polygon A1, A2 ... An circle. To do this, we construct the middle perpendiculars a and b to the segments A1 A2 and A2 A3 (in the figure n \u003d 4). They intersect at some point O. A circle with center O of radius OA1 is circumscribed around the polygon A1 A2 ... An. We now construct the midpoints B1, B2, ..., Bn, respectively, of the arcs A1 A2, A2A3, ..., An A1 as follows. Points B1 and B2 are obtained as the intersection points of lines a and b with arcs A1 A2 and A2 A3. To build point B3, draw a circle with center A3 of radius A3 B2. One of the points of intersection of this circle with the circumscribed circle is point B2, and the other is the desired point B3. The points B4, ..., Bn are constructed similarly. Connecting each of the points B1, B2, ..., Bn by segments with the ends of the corresponding arc, we obtain a 2n-gon A1B1A2B2A3 ... An Bn, which is correct by virtue of the theorem on a polygon inscribed in a circle

In the figure, a regular octagon A1B1A2 ... B4 is constructed using this regular quadrilateral A1A2A3A4. So, if we can construct a regular n-gon with a compass and a ruler, where n is a given positive integer, then we can construct a regular 2n-gon, 4n-gon and, in general, a (2 ^ k * n) -gon, where k is any natural number. The famous German mathematician K. F. Gauss (1777-1855) proved the following interesting theorem: The construction of a regular n-gon using a ruler and compass is possible if and only if the number n has the following factorization: n \u003d 2 ^ m * 2 * p1 * p2 ... ps, where m is a non-negative integer, and p1, p2, ..., ps are different primes of the form 2 ^ 2 ^ k + 1. Let us consider examples of the application of this theorem. For m \u003d 0, s \u003d 1, the number n has the form n \u003d 2 ^ 2 ^ k +1. For values \u200b\u200bof k equal to 0, 1, 2, 3, 4, we obtain n \u003d 3, n \u003d 5, n \u003d 17, n \u003d 257, n \u003d 65 537. For m \u003d 0, s \u003d 2, we have n \u003d p1p2. If, for example, p1 \u003d 3, p2 \u003d 5, then n \u003d 15. Therefore, according to the Gauss theorem, we can construct a regular 15-gon with a pair of compasses and a ruler, as we will see later. The number 7 is prime, but it is not a number of the form 2 ^ 2 ^ k +1, therefore, using a compass and a ruler, you cannot construct a regular heptagon. In the same way, you cannot build a regular heptagon. Finally, we note that the number 360 \u003d 2 ^ 3 * 3 ^ 2 * 5 does not satisfy the Gauss theorem, since the prime number 3 is included in the factor two times. Consequently, a regular 360-gon cannot be built with a pair of compasses and a ruler. In other words, you cannot divide a circle into 360 equal parts, and therefore you cannot build a 1 ° angle with a compass and a ruler.

Task number 1. Building a regular hexagon and triangle.

According to the formula an \u003d 2R * sin180 ° / n, the side AB of a regular hexagon is equal to the radius R of the circumscribed circle. Therefore, if an arbitrary segment PQ is given, then to construct a regular hexagon whose sides are equal to PQ, it is enough to construct a circle of radius PQ, take an arbitrary point A on it and, without changing the compass solution, mark points B, C, D on this circle successively. E, F so that AB \u003d BC \u003d ... \u003d EF \u003d PQ. After drawing the segments AB, BC, CD, DE, EF, FA, we obtain the hexagon ABCDEF, which, according to the theorem on a regular polygon, is regular, and its sides are equal to the segment PQ.

Let a w-given circle be centered at a point O and a radius R. Draw a diameter AC through the point O and draw a middle perpendicular to this diameter that intersects the circle w at two points B and D. Now we connect in series points A, B, C and D. ABCD-required square.

In order to build a regular octagon, you must first build a regular quadrangle, for example, A1A3A5A7-square, then build the bisectors of the angles A1OА3, А3OА5, А5OА7, А7OА1, which intersect the circle at points A2, A4, A6, A8, respectively, then connect the points A1 in series , A2, A3, A4, A5, A6, A7, A8. A1A2 ... A8-required octagon.

Constructed with a compass and a ruler - a section of Euclidean geometry, known since ancient times.

The following operations are possible in construction problems:

Simple example

Mark an arbitrary point on the plane, a point on one of the constructed lines, or the intersection point of two constructed lines.
Using a compass, draw a circle centered at the constructed point with a radius equal to the distance between the two already constructed points.
Using a ruler, draw a line through two constructed points.

In this case, the compass and ruler are considered ideal tools, in particular

The line has no divisions and has only one side of infinite length.
The compass can have an arbitrarily large solution.

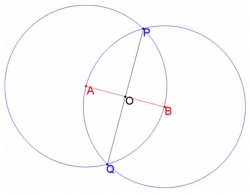
Task 3. Using a compass and a ruler, break a given segment AB into two equal parts. One solution is shown in the figure:

Using a compass, draw a circle centered at point A with radius AB.
Draw a circle centered at point B with radius AB.
We find the intersection points of P and Q of the two circles constructed.
Using a ruler, draw a line connecting the points P and Q.
Find the intersection point of AB and PQ. This is the desired midpoint of segment AB.

Regular Polygons

A regular pentagon can be constructed using a compass and a ruler, or by inscribing it into a given circle, or by building on the basis of a given side. This process is described by Euclid in his "Beginnings" about 300 BC. e. Here is one of the methods for constructing a regular pentagon in a given circle:

1. Build a circle into which the pentagon will be inscribed and designate its center as O. (This is the green circle in the diagram on the right). 2. On the circle, select point A, which will be one of the vertices of the pentagon. Draw a straight line through O and A. 3. Draw a straight line perpendicular to the line OA passing through point O. Mark its one intersection with the circle as point B. 4. Draw point C in the middle between O and B. 5. Draw a circle centered in C through point A. Designate its intersection with the straight line OB (inside the original circle) as point D. 6. Draw a circle centered at A through point D. Designate its intersection with the original (green circle) as points E and F. 7. Draw a circle with center in E through point A. Denote its other intersection with ne then initial circumference as the point G. 8. Carry out a circle centered at F through the point A. Mark its intersection with another circle as the initial point H. 9. Construct regular pentagon AEGHF.

Insoluble tasks

The following three construction tasks were set back in antiquity:

Trisection of an angle - split an arbitrary angle into three equal parts.
Doubling a cube - construct a segment that is an edge of a cube twice as large as a cube with a given edge.
Squaring a circle - build a square equal in area to a given circle.

Only in the XIX century it was proved that all three tasks are not solvable by a pair of compasses and a ruler. The question of the possibility of construction is completely solved by algebraic methods based on Galois theory.

Another well-known unsolvable problem with the help of compass and ruler is the construction of a triangle according to three given ones.

1. Kolmogorov A.N. Parquet made of regular polygons. Quantum Magazine No. 3, 1970

2. Shashkin Yu.A. Parquet floors.

3. Sovetkov P.I., Plum M.V., Khokhlov D.N. Geometric parquet on a computer screen. The journal "Computer Science and Education", 9-2002.

4. Based on materials from the book: W. Ball, G. Coxeter. Math essays and entertainment. Per. from English - M .: "Mir", 1986. - 474 p. with silt.

Edited by Ivanitskaya V.P. - M .: State educational and pedagogical publishing house of the Ministry of Education of the RSFSR, 1959. - 272 p.
Download (direct link) : egnnsholaster1959.djvu Previous 1 .. 50\u003e .. \u003e\u003e Next

§ 53. Constructions by one compass

In § 14 we already talked about constructions with the help of one compass. Let us prove now that all constructions by a compass and a ruler can be performed by one compass. To do this, we use the inversion transformation that we examined in chapter VI.

First of all, we show how to use one compass to construct a point inverse to a given relative to a given circle.

Let A be the given point, and O the circle of inversion.

Case 1. OA\u003e y, where r is the radius of the circle of inversion (Fig. 150 a, 150 b).

We construct a circle of radius AO centered at A \\ from the points of its intersection with the circle O (points P and Q) 9

as centers, we construct circles of radius r. These last two circles, except for point O, intersect at some point A "", which will be the desired one.

Indeed, the points O9 A Yi A "lie on one straight line, like points equidistant from the points PhQ. In addition, AOPA is oodl," since these triangles are isosceles and have a common angle at the vertex O. Hence:

or OA "OA \u003d OP2 \u003d r2, that is, A and A" are mutually inverse points.

Heck. 150 a

Heck. 150 b

Case 2. OA<

We choose a positive integer n such that n - OA\u003e y (which

always possible due to the axiom of Archimedes). On the ray OA, we take point B so that OB \u003d n - OA (Fig. 151). We construct a point S ", inverse to point B, and on the ray OA

point A "so that \u003d n-OB. Then we have:

OA "\u003d OA - p-OB" \u003d \u003d (p-OA) -OV "- \u003d \u003d OB-OB" \u003d r \\

that is, point A is inverse to Devil. 151

Since with the help of one compass we can double the segment (§ 14), then all the constructions in this case we can also carry out with the help of one compass.

We show now how to use one compass to build the center of a circle passing through the three given points O1 A and B (Fig. 152).

We construct a circle centered at point O and take it as the inversion circle. Then we construct the points A "and B", inverse to the given points A and B (which can be done with one compass). In order to simplify the drawing, we take the inversion circle passing through point A. Then points A and A "coincide. Using one compass, we construct point M1 symmetric to point O with respect to line AB". Finally, we construct the point / C inverse to M.

By construction, the points O1 K and M lie on the same line and OK-OM \u003d OA2. From here:

The triangles OAK and OAM are similar, since ^ AOM they have in common, and the sides enclosing it are proportional to

us. Therefore ^ OAK \u003d ^ OMA. By construction, OA \u003d MA. Therefore, OK \u003d AK- Considering the triangles OMB "and OKB1, we also prove that they are similar and KB \u003d OK- Thus, the point K is the center of the desired circle.

To construct a circle inverse to a given circle, take three arbitrary points A, B and C on the last one, construct points A ", B" and C inverse to them and draw a circle through them. All the constructions necessary for this can be performed by one compass.

If a line is given by two points A and B1, then to construct a circle inverse to it (we assume that the line AB does not pass through the center of inversion), construct points A "and B", mutually inverse to points A and B1 and draw a circle through points A ", In "and the center of inversion. All the constructions necessary for this can also be performed by one compass.

We now consider the problem of constructing with one compass a point of intersection of a circle C and a line defined by points A and B.

We take an arbitrary circle so that its center does not lie on the line AB and on the circle C1 and take this circle for the inversion circle. Then we construct circles C and K "inverse of the given circle C and the given line AB. Let M" and N "be the intersection points of the circles C and K". Then the points MnN1 inverse to them are the desired ones. These points, therefore, can be built using only compasses.

If we give two lines AB and CD1 given by the points A1 BnC1D1, then we construct circles inverse to them, find their intersection point M "different from the center of inversion, and construct the point M1 opposite the point LG. Point M will be the desired intersection point of lines AB and CD.

This implies the theorem of Mor à Mascheroni mentioned in § 14: All construction problems solvable by a compass and a ruler are also solvable by one compass.

The general method for solving problems with one compass follows from the proof of this theorem. It goes without saying that specific tasks may have simpler solutions.

When finding the intersection points of the circle and the line, it is convenient to take this circle as the inversion circle. The circle inverse to the line AB intersects

with a circle C at the same points X and Y1 as the line AB (Fig. 153). To construct its center, we construct the point M1 symmetric to the center C with respect to the line AB1 and the point / C inverse M. The point K is the center of the circle inverse to the line AB. It remains to build this circle (its radius is a segment of the CS) and the points of its intersection with this circle.

This construction, as you can see, is justified by the Devil. 153 above when solving the problem of constructing a circle passing through three given points. If the center of the circle lies on the line AB1, this construction is not applicable.

Instruction manual

Mark the points at which the arc intersects the circle as C and C1.

Use a ruler to connect the points C and C1 with a line.

Mark the point at which the line between points C and C1 intersects the diameter of the circle AB as D.

Using a compass, set the distance between points C and D around the circle 7 times. To do this, place the tip of the compass in an arbitrary place on the circle, for example, to point A. Mark any one point on the circle with the drawing part of the compass. Place the tip of the compass at the marked point and mark the next point in the same way. Mark the entire circumference in this way.

Using a ruler and a pencil, connect all the marked points on the circle with its center at point O.

To construct regular polygons, the technique of dividing a circle into equal parts is very often used. Basically, circle can be shared with a protractor. But most often this technique is inconvenient.

Instruction manual

Smash circle into four equal parts is very simple, this is a trivial task. To do this, simply draw two axial lines perpendicular to each other. Points at the intersection of these lines with circleand divide it into four parts. More often it becomes necessary to divide circle not in four, but in eight equal parts. In order to do this, it will be necessary to divide the arc, which is one quarter of the circle, into two equal parts. Then take a pair of compasses and dissolve it to the distance indicated in red in the image. Now it remains just to postpone this distance from each of the four points obtained earlier.

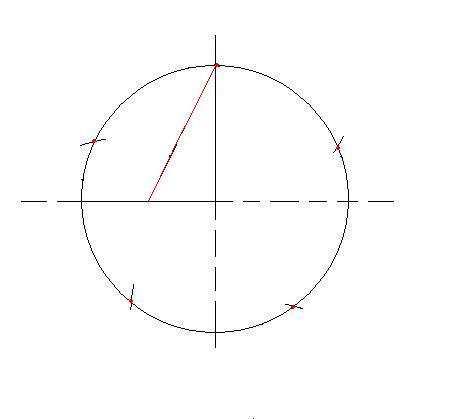
In order to smash circle into three equal parts, spread the legs of the compass into a circle radius. After that, set the compass needle at any intersection of the center lines and the circle. Draw a thin line of auxiliary circle. Three equal parts are formed by the intersection points of the main and auxiliary circles, as well as the point that lies on the center line, or rather on its opposite end.

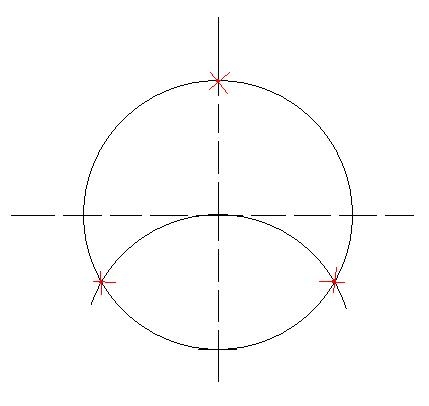
And if you need to divide circle into six equal parts, then you need to do almost everything the same. The only difference is that these steps must be repeated for another center line. In this case, we get six points on the circle at once, as shown in the figure.

Very often there is a need to divide circle into five equal parts. This is also not difficult to do. First you need to divide the radius on the center line into two equal parts. It is at this point that you need to put the needle of the compass. The stylus must be taken to the point of intersection of the circle and the center line perpendicular to this radius. This can be clearly seen in the figure. On it, this distance is depicted in red. Put this distance on the circle. You need to start from the centerline, and then transfer the needle to the new resulting intersection point. To smash circle in ten parts, repeat all the above steps in a mirror.

Division of a circle into equal parts is usually used to construct regular polygons. In principle, you can share circle to pieces with a protractor, but sometimes it is inconvenient and inaccurate.

Instruction manual

To split circle into six parts, do the same for the other axial. Then we get six points on the circle.

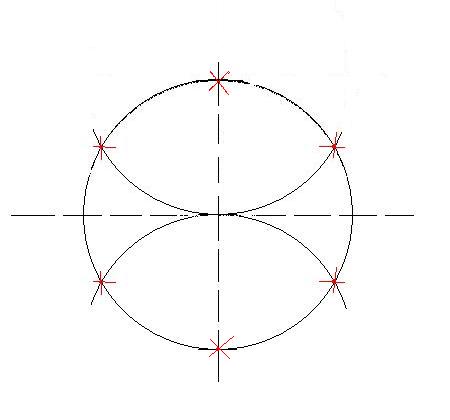
Division of a circle into four parts is a trivial task. Four points at the intersection of two perpendicular axial and circles will divide this circle into four equal parts. To split circle into 8 parts, it is necessary to divide the arc corresponding to 1/4 of the circle in half. Then dilute the compass to the distance indicated in red in the figure and set aside this distance from the four points already obtained.

To split circle into five equal parts, to start, divide the radius on the center line in half. At this point, set the compass needle, and lead to lead to the intersection of the axial and circumferential perpendicular to this radius. In the figure, this distance is shown in red. Put this distance on the circle, starting with the axial, and then transferring the compass to the resulting intersection point.
Repeat all these steps to mirror. circle into 10 identical parts.

Circle measurement

The fact that our planet has the shape of a ball was known to scientists engaged in research in the field of geology for a long time. That is why the first measurements of the magnitude of the circumference of the earth's surface concerned the longest parallel of the Earth - the equator. This value, scientists believed, can be considered correct for any other method of measurement. For example, it was believed that if you measure the circumference of the planet on the longest meridian, the resulting figure will be exactly the same.

Such an opinion existed until the XVIII century. However, scientists of the leading scientific institution of that time - the French Academy - were of the opinion that this hypothesis is incorrect, and the form that the planet has is not entirely correct. Therefore, in their opinion, the circumference along the longest meridian and along the longest parallel will differ.

In evidence in 1735 and 1736, two scientific expeditions were undertaken that proved the truth of this assumption. Subsequently, the magnitude of the difference between these two lengths was established - it amounted to 21.4 kilometers.

Circumference

Currently, the circumference of planet Earth has been repeatedly measured, not by extrapolating the length of a particular segment of the earth's surface to its full size, as was done before, but using modern high-precision technologies. Thanks to this, it was possible to establish the exact circumference along the longest meridian and the longest parallel, as well as to clarify the magnitude of the difference between these parameters.

So, today in the scientific community, as the official value of the circumference of planet Earth along the equator, that is, the longest parallel, it is customary to cite a figure of 40,075.70 kilometers. Moreover, a similar parameter, measured by the longest meridian, that is, the circumference passing through the earth's poles, is 40008.55 kilometers.

Thus, the difference between the circumference is 67.15 kilometers, and the equator is the longest circumference of our planet. In addition, such a difference means that one degree of the geographic meridian is somewhat shorter than one degree of the geographic parallel.

Sources:

how to divide a square into 7 squares