The equation of the oblique asymptote of the graph of the function has the form. Find the asymptotes of the graph of the function. So what is the asymptote

The asymptote of the graph of the function y = f (x) is a straight line that has the property that the distance from the point (x, f (x)) to this straight line tends to zero with an unlimited distance from the origin of the graph point.

Figure 3.10. graphical examples of vertical, horizontal and oblique asymptotes are given.

Finding the asymptotes of the graph is based on the following three theorems.

The vertical asymptote theorem. Let the function y \u003d f (x) be defined in some neighborhood of the point x 0 (possibly excluding this point itself) and at least one of the one-sided limits of the function be equal to infinity, i.e. Then the line x \u003d x 0 is the vertical asymptote of the graph of the function y \u003d f (x).

Obviously, the line x \u003d x 0 cannot be a vertical asymptote if the function is continuous at the point x 0, since in this case . Therefore, vertical asymptotes should be sought at the discontinuity points of a function or at the ends of its domain.

Theorem on the horizontal asymptote. Let the function y \u003d f (x) be defined for sufficiently large x and there be a finite limit of the function . Then the line y = b is the horizontal asymptote of the graph of the function.

Comment. If only one of the limits is finite, then the function has a left-hand or right-hand horizontal asymptote, respectively.

In the event that , the function may have an oblique asymptote.

Oblique asymptote theorem. Let the function y = f(x) be defined for sufficiently large x and there be finite limits . Then the line y = kx + b is an oblique asymptote of the graph of the function.

Without proof.

The oblique asymptote, as well as the horizontal one, can be right-handed or left-handed if the basis of the corresponding limits is infinity of a certain sign.

The study of functions and the construction of their graphs usually includes the following steps:

1. Find the domain of the function.

2. Investigate the function for even-odd.

3. Find the vertical asymptotes by examining the discontinuity points and the behavior of the function on the boundaries of the domain of definition, if they are finite.

4. Find horizontal or oblique asymptotes by examining the behavior of the function at infinity.

5. Find extrema and intervals of monotonicity of the function.

6. Find the convexity intervals of the function and the inflection points.

7. Find points of intersection with the coordinate axes and, possibly, some additional points that refine the graph.

Function differential

It can be proved that if a function has a limit equal to a finite number for a certain base, then it can be represented as the sum of this number and an infinitesimal value for the same base (and vice versa): .

Let's apply this theorem to a differentiable function: .

Thus, the increment of the function Dy consists of two terms: 1) linear with respect to Dx, i.e. f`(x)Dx; 2) non-linear with respect to Dx, i.e. a(Dx)Dx. At the same time, since , this second term is an infinitesimal of a higher order than Dx (as Dx tends to zero, it tends to zero even faster).

The function differential is the main, linear with respect to Dx part of the increment of the function, equal to the product of the derivative and the increment of the independent variable dy = f `(x)Dx.

Find the differential of the function y = x.

Since dy = f `(x)Dx = x`Dx = Dx, then dx = Dx, i.e. the differential of an independent variable is equal to the increment of this variable.

Therefore, the formula for the differential of a function can be written as dy = f `(x)dх. That is why one of the symbols for the derivative is the fraction dy/dх.

The geometric meaning of the differential is illustrated
figure 3.11. Take an arbitrary point M(x, y) on the graph of the function y = f(x). Let's give the argument x an increment Dx. Then the function y = f(x) will receive an increment Dy = f(x + Dх) - f(x). Let's draw a tangent to the graph of the function at the point M, which forms an angle a with the positive direction of the x-axis, i.e. f `(x) = tg a. From right triangle MKN
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy.

Thus, the differential of a function is the increment in the ordinate of the tangent drawn to the graph of the function at a given point when x is incremented by Dx.

The properties of a differential are basically the same as those of a derivative:

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v 2 .

However, there is an important property of the differential of a function that its derivative does not have - this is the invariance of the form of the differential.

From the definition of the differential for the function y = f(x), the differential is dy = f`(x)dх. If this function y is complex, i.e. y = f(u), where u = j(x), then y = f and f `(x) = f `(u)*u`. Then dy = f`(u)*u`dx. But for the function
u = j(x) differential du = u`dx. Hence dy = f `(u)*du.

Comparing the equalities dy = f `(x)dх and dy = f `(u)*du, we will make sure that the differential formula does not change if instead of a function of the independent variable x we consider a function of the dependent variable u. This property of the differential is called the invariance (i.e., invariance) of the form (or formula) of the differential.

However, there is still a difference in these two formulas: in the first of them, the differential of the independent variable is equal to the increment of this variable, i.e. dx = Dx, and in the second, the differential of the function du is only the linear part of the increment of this function Du, and only for small Dх du » Du.

This is how a typical task is formulated, and it involves finding ALL asymptotes of the graph (vertical, oblique / horizontal). Although, to be more precise in the formulation of the question, we are talking about a study for the presence of asymptotes (after all, there may not be any at all).

Let's start with something simple:

Example 1

The solution can be conveniently broken down into two parts:

1) First we check if there are vertical asymptotes. The denominator vanishes at , and it is immediately clear that at this point the function suffers an infinite discontinuity , and the straight line given by the equation is the vertical asymptote of the graph of the function . But before drawing such a conclusion, it is necessary to find one-sided limits:

I recall the calculation technique, on which I similarly dwelled in the article on the continuity of a function. break points. In the expression under the limit sign, instead of "x" we substitute . There is nothing interesting in the numerator:
.

But in the denominator it turns out infinitesimal negative number:
, it determines the fate of the limit.

The left-hand limit is infinite, and, in principle, it is already possible to pass a verdict on the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP YOU UNDERSTAND HOW the graph of the function is located and build it CORRECTLY. Therefore, we must also calculate the right-hand limit:

Conclusion: one-sided limits are infinite, which means that the line is a vertical asymptote of the graph of the function at .

First limit finite, which means that it is necessary to “continue the conversation” and find the second limit:

The second limit too finite.

So our asymptote is:

Conclusion: the straight line given by the equation is the horizontal asymptote of the graph of the function at .

To find the horizontal asymptote, you can use the simplified formula:

If there is a finite limit, then the line is a horizontal asymptote of the graph of the function at .

It is easy to see that the numerator and denominator of the function are of the same order of growth, which means that the desired limit will be finite:

Answer :

According to the condition, it is not necessary to complete the drawing, but if the study of the function is in full swing, then we immediately make a sketch on the draft:

Based on the three limits found, try to independently figure out how the graph of the function can be located. Quite difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is built using transformations of the elementary function graph, and readers who have carefully examined Example 21 of this article can easily guess what kind of curve it is.

Example 2

Find asymptotes of the graph of a function

This is a do-it-yourself example. The process, I remind you, is conveniently divided into two points - vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.

In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:

Example 3

Find asymptotes of the graph of a function

Solution: One, two and done:

1) The vertical asymptotes are at the infinite discontinuity points, so you need to check if the denominator vanishes. Let's solve the quadratic equation:

The discriminant is positive, so the equation has two real roots, and work is added significantly =)

In order to further find one-sided limits, it is convenient to factorize the square trinomial:
(for compact notation, "minus" was introduced in the first bracket). For safety net, we will perform a check, mentally or on a draft, opening the brackets.

Let's rewrite the function in the form

Find one-sided limits at the point :

And at the point:

Thus, the straight lines are the vertical asymptotes of the graph of the function under consideration.

2) If you look at the function, it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show it in a short way:

Thus, the straight line (abscissa) is the horizontal asymptote of the graph of this function.

Answer :

The found limits and asymptotes give a lot of information about the graph of the function. Try to mentally imagine the drawing, taking into account the following facts:

Sketch your version of the graph on a draft.

Of course, the found limits do not unambiguously determine the type of graph, and you may make a mistake, but the exercise itself will be of invaluable help in the course of a complete study of the function. The correct picture is at the end of the lesson.

Example 4

Find asymptotes of the graph of a function

Example 5

Find asymptotes of the graph of a function

These are tasks for independent decision. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4, the growth order of the denominator is greater than the growth order of the numerator, and in Example 5, the numerator and denominator are of the same order of growth. In the sample solution, the first function is investigated for the presence of oblique asymptotes in a full way, and the second - through the limit .

Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are "truly tilted". Long awaited general case:

Example 6

Find asymptotes of the graph of a function

Solution: a classic of the genre:

1) Since the denominator is positive, the function is continuous on the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - great! Item #1 is closed.

2) Check the presence of oblique asymptotes:

First limit finite, so let's move on. In the course of calculating the second limit to eliminate the uncertainty “infinity minus infinity”, we reduce the expression to a common denominator:

The second limit too finite, therefore, the graph of the function under consideration has an oblique asymptote:

Conclusion :

Thus, for the graph of the function infinitely close approaches a straight line:

Note that it intersects its oblique asymptote at the origin, and such intersection points are quite acceptable - it is important that "everything is normal" at infinity (actually, it is there that the discussion of asymptotes comes up).

Example 7

Find asymptotes of the graph of a function

Decision: there is nothing much to comment on, so I will draw up an approximate sample of a final solution:

1) Vertical asymptotes. Let's explore the point.

The straight line is the vertical asymptote for the plot at .

2) Oblique asymptotes:

The straight line is the oblique asymptote for the graph at .

Answer :

The found one-sided limits and asymptotes allow us to assume with high certainty what the graph of this function looks like. Correct drawing at the end of the lesson.

Example 8

Find asymptotes of the graph of a function

This is an example for an independent solution, for the convenience of calculating some limits, you can divide the numerator by the denominator term by term. And again, analyzing the results, try to draw a graph of this function.

Obviously, the owners of "real" oblique asymptotes are the graphs of those fractional-rational functions whose highest degree of the numerator is one greater than the highest degree of the denominator. If more, there will be no oblique asymptote (for example, ).

But other miracles happen in life:

Example 9

Solution: the function is continuous on the entire number line, which means that there are no vertical asymptotes. But there may well be slopes. We check:

I remember how I came across a similar function at the university and simply could not believe that it had an oblique asymptote. Until I calculated the second limit:

Strictly speaking, there are two uncertainties here: and , but one way or another, you need to use the solution method, which is discussed in Examples 5-6 of the article on increased complexity limits. Multiply and divide by the conjugate expression to use the formula:

Answer :

Perhaps the most popular oblique asymptote.

Until now, infinity has been “cut with the same brush”, but it happens that the graph of a function has two different oblique asymptotes at and at:

Example 10

Examine the graph of a function for asymptotes

Decision: the radical expression is positive, which means that the domain of definition is any real number, and there cannot be vertical sticks.

Let's check if oblique asymptotes exist.

If "x" tends to "minus infinity", then:
(when introducing "x" under the square root, you must add a "minus" sign so as not to lose the negative denominator)

It looks unusual, but here the uncertainty is "infinity minus infinity." Multiply the numerator and denominator by the adjoint expression:

Thus, the straight line is the oblique asymptote of the graph at .

With "plus infinity" everything is more trivial:

And the straight line - at .

Answer :

If ;
, If .

I can't resist the graphic image:

This is one of the branches of hyperbole.

It is not uncommon for the potential presence of asymptotes to be initially limited to the domain of the function:

Example 11

Examine the graph of a function for asymptotes

Solution: it is obvious that, therefore, we consider only the right half-plane, where there is a graph of the function.

1) The function is continuous on the interval, which means that if the vertical asymptote exists, then it can only be the y-axis. We study the behavior of the function near the point on right:

Please note that there is NO uncertainty here (attention was focused on such cases at the beginning of the article Methods for Solving Limits).

Thus, the straight line (y-axis) is the vertical asymptote for the graph of the function at .

2) The study of the oblique asymptote can be carried out in full, but in the article L'Hopital's Rules, we found out that a linear function of a higher order of growth than a logarithmic one, therefore: (see Example 1 of the same lesson).

Conclusion: the abscissa axis is the horizontal asymptote of the graph of the function at .

Answer :

If ;
, If .

Drawing for clarity:

Interestingly, a seemingly similar function has no asymptotes at all (those who wish can check this).

Two final self-study examples:

Example 12

Examine the graph of a function for asymptotes

To check for vertical asymptotes, you first need to find the domain of the function , and then calculate a pair of one-sided limits at "suspicious" points. Oblique asymptotes are also not excluded, since the function is defined to "plus" and "minus" infinity.

Example 13

Examine the graph of a function for asymptotes

And here there can only be oblique asymptotes, and the directions , should be considered separately.

I hope you found the right asymptote =)

I wish you success!

Solutions and answers:

Example 2:Solution :
. Let's find one-sided limits:

Straight is the vertical asymptote of the graph of the function at .
2) Oblique asymptotes.

Straight .
Answer :

Drawingto Example 3:

Example 4:Solution :
1) Vertical asymptotes. The function suffers an infinite break at a point . Let's calculate one-sided limits:

Note: An infinitesimal negative number to an even power is equal to an infinitesimal positive number: .

Straight is the vertical asymptote of the graph of the function.
2) Oblique asymptotes.

Straight (abscissa) is the horizontal asymptote of the graph of the function at .
Answer : . .
So, at the graph has no oblique asymptote.

Thus, the direct is the horizontal asymptote of the graph of this function at .
Answer: abscissa at .

Higher mathematics for correspondence students and not only >>>

(Go to main page)

Function nulls. Function constancy intervals.

Spacing Method

Much of the material relating to derivatives and the study of functions traditionally belongs to the school curriculum, and this article is no exception to the rule. Today we will practice finding zeros and constant-sign intervals of a function, and we will also analyze in detail the method of intervals, which can be compared with reliable reinforcement in the walls of the topic under consideration.

If your building design is in the excavation stage, please start with an introductory lesson on feature graphs. In addition, it is advisable to familiarize yourself with the articles Domain of definition of a function, Graph asymptotes, and, in essence, the information on this page is a logical continuation. The material, of course, will be useful to high school students.

In July 2020, NASA launches an expedition to Mars. The spacecraft will deliver to Mars an electronic carrier with the names of all registered members of the expedition.

Registration of participants is open. Get your ticket to Mars at this link.

If this post solved your problem or you just liked it, share the link to it with your friends on social networks.

One of these code options should be copied and pasted into your web page code, preferably between the tags and or right after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically tracks and loads the latest versions of MathJax. If you insert the first code, then it will need to be updated periodically. If you paste the second code, then the pages will load more slowly, but you will not need to constantly monitor MathJax updates.

The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the load code above into it, and place the widget closer to the beginning of the template (by the way, this is not necessary at all , since the MathJax script is loaded asynchronously). That's all. Now learn the MathML, LaTeX, and ASCIIMathML markup syntax and you're ready to embed math formulas into your web pages.

Another New Year's Eve... frosty weather and snowflakes on the window glass... All this prompted me to write again about... fractals, and what Wolfram Alpha knows about it. On this occasion, there is an interesting article in which there are examples of two-dimensional fractal structures. Here we will consider more complex examples of three-dimensional fractals.

A fractal can be visualized (described) as a geometric figure or body (meaning that both are a set, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, it is a self-similar structure, considering the details of which, when magnified, we will see the same shape as without magnification. Whereas in the case of an ordinary geometric figure (not a fractal), when zoomed in, we will see details that have a simpler shape than the original figure itself. For example, at a sufficiently high magnification, part of an ellipse looks like a straight line segment. This does not happen with fractals: with any increase in them, we will again see the same complex shape, which with each increase will be repeated again and again.

Benoit Mandelbrot, the founder of the science of fractals, in his article Fractals and Art for Science wrote: "Fractals are geometric shapes that are as complex in their details as they are in their overall form. That is, if part of the fractal will be enlarged to the size of the whole, it will look like the whole, or exactly, or perhaps with a slight deformation.

Definition. An asymptote of a graph of a function is a line that has the property that the distance from the point of the graph of the function to this line tends to zero with an unlimited distance from the origin of the graph point.

According to the methods of finding them, three types of asymptotes are distinguished: vertical, horizontal, oblique.

Obviously, horizontal ones are special cases of inclined ones (for ).

Finding the asymptotes of the function graph is based on the following statements.

Theorem 1. Let the function be defined at least in some semi-neighborhood of the point and let at least one of its one-sided limits be infinite at this point, i.e. equal. Then the straight line is the vertical asymptote of the graph of the function.

Thus, the vertical asymptotes of the function graph should be sought at the discontinuity points of the function or at the ends of its domain of definition (if these are finite numbers).

Theorem 2. Let the function be defined for argument values that are sufficiently large in absolute value, and there is a finite limit of the function . Then the line is the horizontal asymptote of the graph of the function.

It may happen that , A , and are finite numbers, then the graph has two different horizontal asymptotes: left-handed and right-handed. If only one of the finite limits or exists, then the graph has either one left-handed or one right-handed horizontal asymptote.

Theorem 3. Let the function be defined for values of the argument that are sufficiently large in absolute value, and there are finite limits And . Then the straight line is the oblique asymptote of the graph of the function.

Note that if at least one of these limits is infinite, then there is no oblique asymptote.

The oblique asymptote, like the horizontal one, can be one-sided.

Example. Find all the asymptotes of the function graph.

Solution .

The function is defined with . Let us find its one-sided limits at points.

Because And (the other two one-sided limits can no longer be found), then the lines are the vertical asymptotes of the graph of the function.

Compute

(apply L'Hopital's rule) = .

So the line is a horizontal asymptote.

Since the horizontal asymptote exists, we are no longer looking for oblique asymptotes (they do not exist).

Answer: The graph has two vertical and one horizontal asymptotes.

General Function Study y = f(x).

Function scope. Find its domain D(f) . If it is not too difficult, then it is useful to find also the range E(f) . (However, in many cases, the question of finding E(f) is delayed until the extrema of the function are found.)

Special properties of a function. Find out the general properties of the function: even, odd, periodicity, etc. Not every function has such properties as even or odd. A function is certainly neither even nor odd if its domain of definition is asymmetric about the point 0 on the axis Ox. In the same way, for any periodic function, the domain of definition consists either of the entire real axis, or of the union of periodically repeating systems of gaps.

Vertical asymptotes. Find out how the function behaves when the argument approaches the boundary points of the domain of definition D(f) if there are such boundary points. In this case, vertical asymptotes may appear. If the function has such discontinuity points at which it is not defined, then these points are also checked for the presence of vertical asymptotes of the function.

Oblique and horizontal asymptotes. If the scope D(f) includes rays of the form (a;+) or (−;b), then we can try to find oblique asymptotes (or horizontal asymptotes) at x+ or x−, respectively, i.e. find limxf(x). Oblique asymptotes: y = kx + b, where k=limx+xf(x) and b=limx+(f(x)−x). Horizontal asymptotes: y = b, where limxf(x)=b.

Finding the intersection points of the graph with the axes. Finding the point of intersection of the graph with the axis Oy. To do this, you need to calculate the value f(0). Find also the points of intersection of the graph with the axis Ox, why find the roots of the equation f(x) = 0 (or make sure there are no roots). The equation can often be solved only approximately, but the separation of the roots helps to better understand the structure of the graph. Next, you need to determine the sign of the function on the intervals between the roots and break points.

Finding the intersection points of the graph with the asymptote. In some cases, it may be necessary to find characteristic points of the graph that were not mentioned in the previous paragraphs. For example, if the function has an oblique asymptote, then you can try to find out if there are any points of intersection of the graph with this asymptote.

Finding intervals of convexity and concavity. This is done by examining the sign of the second derivative f(x). Find the inflection points at the junctions of the convex and concavity intervals. Calculate the value of the function at the inflection points. If the function has other points of continuity (other than inflection points) at which the second derivative is equal to 0 or does not exist, then at these points it is also useful to calculate the value of the function. Having found f(x) , we solve the inequality f(x)0. On each of the solution intervals, the function will be downward convex. Solving the reverse inequality f(x)0, we find the intervals on which the function is convex upwards (that is, concave). We define inflection points as those points at which the function changes the direction of convexity (and is continuous).

Asymptotes of the graph of a function

The ghost of the asymptote has been wandering around the site for a long time to finally materialize in a single article and delight readers who are puzzled by the full study of the function. Finding the asymptotes of the graph is one of the few parts of the indicated task, which is covered in the school course only in an overview order, since the events revolve around the calculation of the limits of functions, and they still relate to higher mathematics. Visitors who are poorly versed in mathematical analysis, I think the hint is understandable ;-) ... stop-stop, where are you going? Limits are easy!

Examples of asymptotes met immediately in the first lesson on graphs of elementary functions, and now the topic is receiving detailed consideration.

So what is an asymptote?

Imagine variable point, which "travels" along the graph of the function. An asymptote is a straight line to which unlimited close the graph of the function approaches as its variable point goes to infinity.

Note : the definition is meaningful, if you need a formulation in the notation of mathematical analysis, please refer to the textbook.

On a plane, asymptotes are classified according to their natural arrangement:

1) Vertical asymptotes, which are given by an equation of the form, where "alpha" is a real number. The popular representative defines the y-axis itself,
with an attack of mild nausea, we recall hyperbole.

2) Oblique asymptotes are traditionally written as a straight line equation with a slope. Sometimes a special case is singled out as a separate group - horizontal asymptotes. For example, the same hyperbola with asymptote .

Quickly off we go, let's hit the topic with a short automatic burst:

How many asymptotes can a graph of a function have?

None, one, two, three... or an infinite number. We will not go far for examples, we recall elementary functions. Parabola, cubic parabola, sinusoid have no asymptotes at all. The graph of an exponential, logarithmic function has a single asymptote. The arctangent, arccotangent has two of them, and the tangent, cotangent has an infinite number. It is not uncommon for a graph to have both horizontal and vertical asymptotes. Hyperbole, will always love you.

What means ? Vertical asymptotes of a graph of a function

The vertical asymptote of the graph, as a rule, is at the point of infinite discontinuity of the function. It's simple: if at a point the function suffers an infinite break, then the straight line given by the equation is the vertical asymptote of the graph.

Note : note that the notation is used to refer to two completely different concepts. The point is implied or the equation of a straight line - depends on the context.

Thus, to establish the presence of a vertical asymptote at a point, it suffices to show that at least one of the one-sided limits endless. Most often, this is the point where the denominator of the function is equal to zero. In fact, we already found vertical asymptotes in the last examples of the lesson on the continuity of a function. But in some cases there is only one one-sided limit, and if it is infinite, then again - love and favor the vertical asymptote. The simplest illustration: and the y-axis (see Graphs and properties of elementary functions).

The obvious fact also follows from the above: if the function is continuous on , then there are no vertical asymptotes . For some reason, a parabola came to mind. Indeed, where can you “stick” a straight line here? ... yes ... I understand ... the followers of Uncle Freud huddled in hysterics =)

The converse statement is generally not true: for example, the function is not defined on the entire real line, but it is completely deprived of asymptotes.

Oblique asymptotes of a graph of a function

Oblique (as a special case - horizontal) asymptotes can be drawn if the function argument tends to "plus infinity" or "minus infinity". Therefore, the graph of a function cannot have more than two oblique asymptotes. For example, the graph of an exponential function has a single horizontal asymptote at , and the graph of the arc tangent at has two such asymptotes, and different ones.

When the graph here and there approaches the only oblique asymptote, then it is customary to unite “infinities” under a single entry. For example, ... you guessed it right: .

General rule of thumb:

If there are two final limit , then the straight line is the oblique asymptote of the graph of the function at . If at least one of the listed limits is infinite, then there is no oblique asymptote.

Note : the formulas remain valid if "x" tends only to "plus infinity" or only to "minus infinity".

Let us show that the parabola has no oblique asymptotes:

The limit is infinite, so there is no oblique asymptote. Note that in finding the limit no longer needed because the answer has already been received.

Note : if you have (or will have) difficulty understanding the plus-minus, minus-plus signs, please see the help at the beginning of the lesson
about infinitesimal functions, where I told how to correctly interpret these signs.

It is obvious that any quadratic, cubic function, polynomial of the 4th and higher degrees also does not have oblique asymptotes.

And now let's make sure that at the graph also does not have an oblique asymptote. To reveal the uncertainty, we use the L'Hopital rule:
, which was to be verified.

When the function grows indefinitely, however, there is no such straight line to which its graph would approach infinitely close.

Let's move on to the practical part of the lesson:

How to find the asymptotes of a graph of a function?

Example 1

Find asymptotes of the graph of a function

The solution can be conveniently broken down into two parts:

I remind you of the calculation technique, which I similarly discussed in the article Continuity of a function. break points. In the expression under the limit sign, instead of "x" we substitute . There is nothing interesting in the numerator:
.

But in the denominator it turns out infinitesimal negative number:
, it determines the fate of the limit.

Conclusion: one-sided limits are infinite, which means that the line is a vertical asymptote of the graph of the function at .

First limit finite, which means that it is necessary to “continue the conversation” and find the second limit:

The second limit too finite.

So our asymptote is:

Conclusion: the straight line given by the equation is the horizontal asymptote of the graph of the function at .

To find the horizontal asymptote
You can use a simplified formula:

If exists finite limit , then the line is the horizontal asymptote of the graph of the function at .

It is easy to see that the numerator and denominator of the function are of the same order of growth, which means that the desired limit will be finite: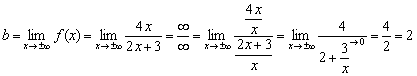

Answer :

Example 2

Find asymptotes of the graph of a function

In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:

Example 3

Find asymptotes of the graph of a function

Solution: One, two and done:

Let's rewrite the function in the form

Find one-sided limits at the point :

And at the point:

Thus, the straight lines are the vertical asymptotes of the graph of the function under consideration.

2) If you look at the function , then it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show it in a short way:

Thus, the straight line (abscissa) is the horizontal asymptote of the graph of this function.

Answer :

The found limits and asymptotes give a lot of information about the graph of the function. Try to mentally imagine the drawing, taking into account the following facts:

Sketch your version of the graph on a draft.

Example 4

Find asymptotes of the graph of a function

Example 5

Find asymptotes of the graph of a function

These are tasks for independent decision. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4, the order of growth of the denominator more than the order of growth of the numerator, and in Example 5 the numerator and denominator are of the same order of growth. In the sample solution, the first function is investigated for the presence of oblique asymptotes in a full way, and the second - through the limit .

Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are "truly tilted". Long awaited general case:

Example 6

Find asymptotes of the graph of a function

Solution: a classic of the genre:

1) Since the denominator is positive, the function is continuous on the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - excellent! Item #1 is closed.

The second limit too finite, therefore, the graph of the function under consideration has an oblique asymptote:

Conclusion :

Thus, for the graph of the function infinitely close approaches a straight line:

Example 7

Find asymptotes of the graph of a function

Decision: there is nothing much to comment on, so I will draw up an approximate sample of a final solution:

1) Vertical asymptotes. Let's explore the point.

The straight line is the vertical asymptote for the plot at .

2) Oblique asymptotes:

The straight line is the oblique asymptote for the graph at .

Answer :

The found one-sided limits and asymptotes allow us to assume with high certainty what the graph of this function looks like. Correct drawing at the end of the lesson.

Example 8

Find asymptotes of the graph of a function

But other miracles happen in life:

Example 9

Example 11

Examine the graph of a function for asymptotes

Solution: obviously , therefore, we consider only the right half-plane, where there is a graph of the function.

Thus, the straight line (y-axis) is the vertical asymptote for the graph of the function at .

2) The study of the oblique asymptote can be carried out in full, but in the article Rules of L'Hospital, we found out that a linear function of a higher order of growth than a logarithmic one, therefore: (see example 1 of the same lesson).

Conclusion: the abscissa axis is the horizontal asymptote of the graph of the function at .

Answer :
, If ;
, If .

Drawing for clarity:

Interestingly, a seemingly similar function has no asymptotes at all (those who wish can check this).

Two final self-study examples:

Example 12

Examine the graph of a function for asymptotes