Ayrımcı, belirsiz bir terimdir. Bu makale, belirli bir polinomun gerçek çözümlere sahip olup olmadığını belirlemesine izin veren bir polinomun ayrımcısını tartışacaktır. Kare polinom için formül cebir ve analiz okul dersinde bulunur. Ayrımcı nasıl bulunur? Denklemi çözmek için ne gerekiyor?
İkinci dereceden bir kare polinom veya denklem denir i * w ^ 2 + j * w + k 0'a eşittir, burada “i” ve “j” sırasıyla birinci ve ikinci katsayılardır, “k” bazen “serbest terim” olarak adlandırılan sabittir ve “w” bir değişkendir. Kökleri, kimliğe dönüştüğü değişkenin tüm değerleri olacaktır. İ, (w - w1) ve (w - w2) çarpımı gibi bir eşitliği 0'a eşit olarak yeniden yazmak mümkündür. Bu durumda, “i” katsayısı kaybolmazsa, sol taraftaki fonksiyonun yalnızca x, w1 veya w2 değerini alırsa. Bu değerler, polinomu sıfıra eşitlemenin sonucudur.
Kare polinomun kaybolduğu değişkenin değerini bulmak için, katsayılarına dayanan ve ayrımcı olarak adlandırılan yardımcı bir yapı kullanırız. Bu tasarım D formülüne göre hesaplanır: j * j - 4 * i * k. Neden kullanılır?
- Geçerli sonuçların olup olmadığını söylüyor.
- Hesaplamalarına yardım eder.
Bu değer, malzeme köklerinin varlığını gösterdiğinden:
- Olumlu ise, gerçek sayılar alanında iki kök bulabilirsiniz.
- Diskriminant sıfıra eşitse, her iki çözelti çakışır. Tek bir çözüm olduğunu söyleyebiliriz, ve bu gerçek sayılar alanından gelir.
- Ayrımcı sıfırdan küçükse, polinomun gerçek kökleri yoktur.
Malzemeyi sabitlemek için yerleşim seçenekleri
Toplam için (7 * w ^ 2; 3 * w; 1) 0'a eşit D formülünü 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 formülünü kullanarak -19 elde ederiz. Sıfırın altındaki bir ayırt edici değer, gerçek çizgide sonuçların olmadığını gösterir.
2 * w ^ 2 - 3 * w + 1 eşdeğeri 0'ı düşünürsekdaha sonra D, (-3) kare eksi (4; 2; 1) sayılarının çarpımı olarak hesaplanır ve 9 - 8'e eşittir, yani 1'dir. Pozitif bir değer, gerçek satırdaki iki sonucu gösterir.

Toplamı alırsak (w ^ 2; 2 * w; 1) ve 0'a eşitlerseD, iki kare eksi (4; 1; 1) sayılarının çarpımı olarak hesaplanır. Bu ifade 4 - 4'e sadeleştirecek ve yok olacaktır. Sonuçların aynı olduğu ortaya çıkıyor. Bu formüle yakından bakarsanız, bunun “tam kare” olduğu anlaşılacaktır. Bu nedenle, eşitlik (w + 1) ^ 2 \u003d 0 şeklinde yeniden yazılabilir. Bu problemin sonucunun “-1” olduğu ortaya çıktı. D'nin 0 olması durumunda, denklemin sol tarafı daima "kare toplamı" formülüne göre ortaya çıkacaktır.
Diskriminantın kök hesaplamasında kullanılması
Bu yardımcı yapı sadece malzeme çözümlerinin sayısını göstermekle kalmaz, aynı zamanda bunları bulmaya da yardımcı olur. İkinci derecenin denklemi için genel hesaplama formülü aşağıdaki gibidir:
w \u003d (-j +/- d) / (2 * i); burada d, 1/2 derecesinin bir ayırıcısıdır.
Diskriminantın sıfırın altında olduğunu, sonra d'nin hayali ve sonuçların hayali olduğunu varsayalım.
D sıfır, sonra D eşittir 1/2 derece de sıfırdır. Çözüm: -j / (2 * i). Yine 1 * w ^ 2 + 2 * w + 1 \u003d 0 olduğunu düşünüyoruz, -2 / (2 * 1) \u003d -1'e eşit sonuçları buluyoruz.
D\u003e 0 olduğunu varsayalım, bu yüzden d gerçek bir sayıdır ve buradaki cevap iki bölüme ayrılmıştır: w1 \u003d (-j + d) / (2 * i) ve w2 \u003d (-j - d) / (2 * i) . Her iki sonuç da geçerli olacaktır. 2 * w ^ 2 - 3 * w + 1 \u003d 0'a bakın. Burada, diskriminant ve d birimleridir. W1'in (3 + 1) bölünmüş (2 * 2) veya 1 ve w2'nin (3 - 1) bölünmüş 2 * 2 veya 1/2 olduğu ortaya çıkıyor.
Kare ifadeyi sıfıra eşitlemenin sonucu algoritmaya göre hesaplanır:
- Geçerli kararların sayısını belirleme.
- Hesaplama d \u003d D ^ (1/2).
- Sonucu (-j +/- d) / (2 * i) formülüne göre bulma.
- Sonucun doğrulama için orijinal eşitliğe değiştirilmesi.
Bazı özel durumlar
Katsayılara bağlı olarak, çözelti biraz basitleştirilebilir. Açıkçası, değişkenin önündeki katsayı sıfıra ikinci dereceye eşitse, doğrusal eşitlik elde edilir. Değişken önündeki katsayı birinci derecede sıfır olduğunda, iki seçenek mümkündür:
- polinom negatif bir serbest terime sahip kareler farkına ayrışır;
- pozitif bir sabit ile gerçek çözümler bulunamaz.
Serbest terim sıfır ise, kökler (0; -j) olacaktır.
Ancak çözüm bulmayı kolaylaştıran başka özel durumlar da var.
İkinci derecenin azaltılmış denklemi
Olarak anılacaktır üst düzey dönemin önündeki katsayının bir olduğu böyle bir kare üçlü. Bu durum için, köklerin toplamının birinci derecedeki değişkenin katsayısına -1 ile çarpıldığını ve ürünün "k" sabitine karşılık geldiğini belirten Vieta teoremi uygulanabilir.
Bu nedenle, ilk katsayı bir ise w1 + w2 -j ve w1 * w2 eşittir k. Böyle bir sunumun doğruluğunu doğrulamak için, birinci formülden w2 \u003d -j - w1 ifade edebilir ve bunu ikinci eşitlik w1 * (-j - w1) \u003d k ile değiştirebiliriz. Sonuç olarak, başlangıç \u200b\u200beşitliği w1 ^ 2 + j * w1 + k \u003d 0 elde edilir.

Dikkat edilmesi gereken önemlii * w ^ 2 + j * w + k \u003d 0, “i” ile bölünerek azaltılabilir. Sonuç şu olacaktır: w ^ 2 + j1 * w + k1 \u003d 0, burada j1 j / i ve k1 k / i'dir.
W1 \u003d 1 ve w2 \u003d 1/2 sonuçları ile önceden çözülmüş 2 * w ^ 2 - 3 * w + 1 \u003d 0'a bir göz atın. Sonuç olarak w ^ 2 - 3/2 * w + 1/2 \u003d 0 olarak ikiye bölmek gerekir. Teorem koşullarının bulunan sonuçlar için geçerli olduğunu doğrulayalım: 1 + 1/2 \u003d 3/2 ve 1 * 1/2 \u003d 1 / 2.
İkinci çarpan bile
Birinci derecedeki (j) bir değişkenin faktörü 2'ye bölünebilirse, o zaman formülü basitleştirebilir ve ayrımcı D / 4 \u003d (j / 2) ^ 2 - i * k'nin dörtte birinde bir çözüm arayabiliriz. w \u003d (-j +/- d / 2) / i çıkıyor, burada d / 2 \u003d D / 4 1/2 gücüne.
İ \u003d 1 ise ve j katsayısı eşitse, çözelti, w değişkeni için katsayının -1 ve yarısının çarpımı, artı / eksi bu yarım karenin kökü eksi “k” sabitidir. Formül: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.
Yüksek Ayrımcı Emir
Yukarıda düşünülen ikinci derecenin trinomialinin ayırt edici özelliği en çok kullanılan özel durumdur. Genel durumda, bir polinomun ayırt edici özelliği bu polinomun köklerinin farklılıklarının çoğaltılmış kareleri. Bu nedenle, sıfıra eşit bir ayırıcı en az iki çoklu çözeltinin varlığını gösterir.
İ * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0 diyelim.
D \u003d j ^ 2 * k ^ 2-4 * i * k ^ 3-4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Diyelim ki ayrımcı sıfırdan büyük. Bu, gerçek sayılar alanında üç kök olduğu anlamına gelir. Sıfırda birden fazla çözüm vardır. D ise< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.
video
Videomuz, ayrımcılığın hesaplanması hakkında ayrıntılı olarak konuşacaktır.
Sorunuza cevap gelmedi mi? Yazarlara bir konu önerin.
Örneğin, üçlü ((3x ^ 2 + 2x-7 \\) için, ayrımcı \\ (2 ^ 2-4 \\ cdot3 \\ cdot (-7) \u003d 4 + 84 \u003d 88 \\) olacaktır. Üçlü \\ (x ^ 2-5x + 11 \\) için, \\ ((- 5) ^ 2-4 \\ cdot1 \\ cdot11 \u003d 25-44 \u003d -19 \\) değerine eşit olacaktır.
Diskriminant \\ (D \\) harfi ile gösterilir ve genellikle çözmede kullanılır. Ayrıca, ayrımcı değerine göre, grafiğin yaklaşık olarak nasıl göründüğünü anlayabilirsiniz (aşağıya bakın).
Ayrımcı ve denklemin kökleri
Ayrımcının değeri ikinci dereceden denklemlerin sayısını gösterir:
- \\ (D \\) pozitifse, denklemin iki kökü olacaktır;
- \\ (D \\) sıfıra eşitse - sadece bir kök;
- \\ (D \\) negatifse, kök yoktur.
Bunu öğrenmenize gerek yok, bu sonuca varmak kolaydır, sadece ayrımcıdan (yani, \\ (\\ sqrt (D) \\)) denklemin köklerini hesaplamak için formüle dahil edildiğini bilerek: \\ (x_ (1) \u003d \\) \\ (\\ .
Eğer ayrımcı pozitifse
Bu durumda, kökü pozitif bir sayıdır, yani \\ (x_ (1) \\) ve \\ (x_ (2) \\) değerlerinden farklı olacaktır, çünkü ilk formülde \\ (\\ sqrt (D) \\) eklendi ve ikincisinde - çıkarılır. Ve iki farklı kökenimiz var.
örnek
: Denklemin köklerini bulun \\ (x ^ 2 + 2x-3 \u003d 0 \\)
karar
:
Cevap : \\ (x_ (1) \u003d 1 \\); \\ (x_ (2) \u003d - 3 \\)
Diskriminant sıfırsa
Ayrımcı sıfır ise kaç kök olacak? Sebep edelim.
Kök formüller şöyle görünür: \\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) ve \\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\). Ayrımcı sıfır ise, kökü de sıfırdır. Sonra ortaya çıkıyor:
\\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + 0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)
\\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b- \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b-0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)
Yani, denklemin köklerinin değerleri çakışacaktır, çünkü sıfır eklemek veya çıkarmak hiçbir şeyi değiştirmez.
örnek
: Denklemin köklerini bulun \\ (x ^ 2-4x + 4 \u003d 0 \\)
karar
:
|
\\ (x ^ 2-4x + 4 \u003d 0 \\) |
Katsayıları yazıyoruz: |
|
|
\\ (a \u003d 1; \\) \\ (b \u003d -4; \\) \\ (c \u003d 4; \\) |
Ayrımcıyı \\ (D \u003d b ^ 2-4ac \\) formülüyle hesaplıyoruz |
|
|
\\ (D \u003d (- 4) ^ 2-4 \\ cdot1 \\ cdot4 \u003d \\) |
Denklemin köklerini bulun |
|
|
\\ (x_ (1) \u003d \\) \\ (\\ frac (- (- 4) + \\ sqrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\) \\ (x_ (2) \u003d \\) \\ (\\ frac (- (- 4) - \\ sqrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\) |
|
İki özdeş kökenimiz var, bu yüzden bunları ayrı ayrı yazmak mantıklı değil - tek olarak yazıyoruz. |
Cevap : \\ (x \u003d 2 \\)
Ayrımcı, belirsiz bir terimdir. Bu makale, belirli bir polinomun gerçek çözümlere sahip olup olmadığını belirlemesine izin veren bir polinomun ayrımcısını tartışacaktır. Kare polinom için formül cebir ve analiz okul dersinde bulunur. Ayrımcı nasıl bulunur? Denklemi çözmek için ne gerekiyor?
İkinci dereceden bir kare polinom veya denklem denir i * w ^ 2 + j * w + k 0'a eşittir, burada “i” ve “j” sırasıyla birinci ve ikinci katsayılardır, “k” bazen “serbest terim” olarak adlandırılan sabittir ve “w” bir değişkendir. Kökleri, kimliğe dönüştüğü değişkenin tüm değerleri olacaktır. İ, (w - w1) ve (w - w2) çarpımı gibi bir eşitliği 0'a eşit olarak yeniden yazmak mümkündür. Bu durumda, “i” katsayısı kaybolmazsa, sol taraftaki fonksiyonun yalnızca x, w1 veya w2 değerini alırsa. Bu değerler, polinomu sıfıra eşitlemenin sonucudur.
Kare polinomun kaybolduğu değişkenin değerini bulmak için, katsayılarına dayanan ve ayrımcı olarak adlandırılan yardımcı bir yapı kullanırız. Bu tasarım D formülüne göre hesaplanır: j * j - 4 * i * k. Neden kullanılır?
- Geçerli sonuçların olup olmadığını söylüyor.
- Hesaplamalarına yardım eder.
Bu değer, malzeme köklerinin varlığını gösterdiğinden:
- Olumlu ise, gerçek sayılar alanında iki kök bulabilirsiniz.
- Diskriminant sıfıra eşitse, her iki çözelti çakışır. Tek bir çözüm olduğunu söyleyebiliriz, ve bu gerçek sayılar alanından gelir.
- Ayrımcı sıfırdan küçükse, polinomun gerçek kökleri yoktur.
Malzemeyi sabitlemek için yerleşim seçenekleri
Toplam için (7 * w ^ 2; 3 * w; 1) 0'a eşit D formülünü 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 formülünü kullanarak -19 elde ederiz. Sıfırın altındaki bir ayırt edici değer, gerçek çizgide sonuçların olmadığını gösterir.
2 * w ^ 2 - 3 * w + 1 eşdeğeri 0'ı düşünürsekdaha sonra D, (-3) kare eksi (4; 2; 1) sayılarının çarpımı olarak hesaplanır ve 9 - 8'e eşittir, yani 1'dir. Pozitif bir değer, gerçek satırdaki iki sonucu gösterir.

Toplamı alırsak (w ^ 2; 2 * w; 1) ve 0'a eşitlerseD, iki kare eksi (4; 1; 1) sayılarının çarpımı olarak hesaplanır. Bu ifade 4 - 4'e sadeleştirecek ve yok olacaktır. Sonuçların aynı olduğu ortaya çıkıyor. Bu formüle yakından bakarsanız, bunun “tam kare” olduğu anlaşılacaktır. Bu nedenle, eşitlik (w + 1) ^ 2 \u003d 0 şeklinde yeniden yazılabilir. Bu problemin sonucunun “-1” olduğu ortaya çıktı. D'nin 0 olması durumunda, denklemin sol tarafı daima "kare toplamı" formülüne göre ortaya çıkacaktır.
Diskriminantın kök hesaplamasında kullanılması
Bu yardımcı yapı sadece malzeme çözümlerinin sayısını göstermekle kalmaz, aynı zamanda bunları bulmaya da yardımcı olur. İkinci derecenin denklemi için genel hesaplama formülü aşağıdaki gibidir:
w \u003d (-j +/- d) / (2 * i); burada d, 1/2 derecesinin bir ayırıcısıdır.
Diskriminantın sıfırın altında olduğunu, sonra d'nin hayali ve sonuçların hayali olduğunu varsayalım.
D sıfır, sonra D eşittir 1/2 derece de sıfırdır. Çözüm: -j / (2 * i). Yine 1 * w ^ 2 + 2 * w + 1 \u003d 0 olduğunu düşünüyoruz, -2 / (2 * 1) \u003d -1'e eşit sonuçları buluyoruz.
D\u003e 0 olduğunu varsayalım, bu yüzden d gerçek bir sayıdır ve buradaki cevap iki bölüme ayrılmıştır: w1 \u003d (-j + d) / (2 * i) ve w2 \u003d (-j - d) / (2 * i) . Her iki sonuç da geçerli olacaktır. 2 * w ^ 2 - 3 * w + 1 \u003d 0'a bakın. Burada, diskriminant ve d birimleridir. W1'in (3 + 1) bölünmüş (2 * 2) veya 1 ve w2'nin (3 - 1) bölünmüş 2 * 2 veya 1/2 olduğu ortaya çıkıyor.
Kare ifadeyi sıfıra eşitlemenin sonucu algoritmaya göre hesaplanır:
- Geçerli kararların sayısını belirleme.
- Hesaplama d \u003d D ^ (1/2).
- Sonucu (-j +/- d) / (2 * i) formülüne göre bulma.
- Sonucun doğrulama için orijinal eşitliğe değiştirilmesi.
Bazı özel durumlar
Katsayılara bağlı olarak, çözelti biraz basitleştirilebilir. Açıkçası, değişkenin önündeki katsayı sıfıra ikinci dereceye eşitse, doğrusal eşitlik elde edilir. Değişken önündeki katsayı birinci derecede sıfır olduğunda, iki seçenek mümkündür:
- polinom negatif bir serbest terime sahip kareler farkına ayrışır;
- pozitif bir sabit ile gerçek çözümler bulunamaz.
Serbest terim sıfır ise, kökler (0; -j) olacaktır.
Ancak çözüm bulmayı kolaylaştıran başka özel durumlar da var.
İkinci derecenin azaltılmış denklemi
Olarak anılacaktır üst düzey dönemin önündeki katsayının bir olduğu böyle bir kare üçlü. Bu durum için, köklerin toplamının birinci derecedeki değişkenin katsayısına -1 ile çarpıldığını ve ürünün "k" sabitine karşılık geldiğini belirten Vieta teoremi uygulanabilir.
Bu nedenle, ilk katsayı bir ise w1 + w2 -j ve w1 * w2 eşittir k. Böyle bir sunumun doğruluğunu doğrulamak için, birinci formülden w2 \u003d -j - w1 ifade edebilir ve bunu ikinci eşitlik w1 * (-j - w1) \u003d k ile değiştirebiliriz. Sonuç olarak, başlangıç \u200b\u200beşitliği w1 ^ 2 + j * w1 + k \u003d 0 elde edilir.

Dikkat edilmesi gereken önemlii * w ^ 2 + j * w + k \u003d 0, “i” ile bölünerek azaltılabilir. Sonuç şu olacaktır: w ^ 2 + j1 * w + k1 \u003d 0, burada j1 j / i ve k1 k / i'dir.
W1 \u003d 1 ve w2 \u003d 1/2 sonuçları ile önceden çözülmüş 2 * w ^ 2 - 3 * w + 1 \u003d 0'a bir göz atın. Sonuç olarak w ^ 2 - 3/2 * w + 1/2 \u003d 0 olarak ikiye bölmek gerekir. Teorem koşullarının bulunan sonuçlar için geçerli olduğunu doğrulayalım: 1 + 1/2 \u003d 3/2 ve 1 * 1/2 \u003d 1 / 2.
İkinci çarpan bile
Birinci derecedeki (j) bir değişkenin faktörü 2'ye bölünebilirse, o zaman formülü basitleştirebilir ve ayrımcı D / 4 \u003d (j / 2) ^ 2 - i * k'nin dörtte birinde bir çözüm arayabiliriz. w \u003d (-j +/- d / 2) / i çıkıyor, burada d / 2 \u003d D / 4 1/2 gücüne.
İ \u003d 1 ise ve j katsayısı eşitse, çözelti, w değişkeni için katsayının -1 ve yarısının çarpımı, artı / eksi bu yarım karenin kökü eksi “k” sabitidir. Formül: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.
Yüksek Ayrımcı Emir
Yukarıda düşünülen ikinci derecenin trinomialinin ayırt edici özelliği en çok kullanılan özel durumdur. Genel durumda, bir polinomun ayırt edici özelliği bu polinomun köklerinin farklılıklarının çoğaltılmış kareleri. Bu nedenle, sıfıra eşit bir ayırıcı en az iki çoklu çözeltinin varlığını gösterir.
İ * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0 diyelim.
D \u003d j ^ 2 * k ^ 2-4 * i * k ^ 3-4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Diyelim ki ayrımcı sıfırdan büyük. Bu, gerçek sayılar alanında üç kök olduğu anlamına gelir. Sıfırda birden fazla çözüm vardır. D ise< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.
video
Videomuz, ayrımcılığın hesaplanması hakkında ayrıntılı olarak konuşacaktır.
Sorunuza cevap gelmedi mi? Yazarlara bir konu önerin.
Önemli! Çokluğun eşit köklerinde, işlev işareti değiştirmez.
Dikkat! Cebirin okul dersindeki herhangi bir doğrusal olmayan eşitsizlik, aralık yöntemi kullanılarak çözülmelidir.
Size detaylı bir teklif aralık yöntemi ile eşitsizliklerin çözümü için algoritmaaşağıdaki hatalardan kaçınabilirsiniz doğrusal olmayan eşitsizliklerin çözümü.
İkinci dereceden denklemleri negatif ayrımcılarla çözme
Bildiğimiz gibi
ben 2 = - 1.
aynı anda
(- ben ) 2 = (- 1 ben ) 2 = (- 1) 2 ben 2 = -1.
Böylece, - 1'in kare kökünün en az iki değeri vardır, yani ben ve - ben . Ama belki kareleri eşit olan bazı karmaşık sayılar vardır - 1?
Bu soruyu açıklığa kavuşturmak için karmaşık bir sayının karesini varsayalım a + bi eşittir - 1. Sonra
(a + bi ) 2 = - 1,
ve 2 + 2abi - b 2 = - 1
İki karmaşık sayı, yalnızca gerçek parçaları ve hayali parçaların katsayıları eşitse eşittir. bu nedenle
| { | ve 2 - b 2 = - 1 ab = 0 (1) |
Sistemin (1) ikinci denklemine göre, sayılardan en az biri ve ve b sıfır olmalıdır. eğer b \u003d 0, sonra ilk denklem verir ve 2 \u003d - 1. Sayı ve geçerli ve bu nedenle ve 2 > 0. Negatif olmayan sayı ve 2, negatif bir sayıya eşit olamaz - 1. Bu nedenle, eşitlik b Bu durumda \u003d 0 mümkün değildir. Kabul edilmesi gereken, ve \u003d 0, fakat sonra elde ettiğimiz sistemin ilk denkleminden: - b 2 = - 1, b \u003d ± 1.
Bu nedenle, kareleri -1 olan karmaşık sayılar yalnızca sayılardır ben ve - ben , Şartlı olarak, bu şöyle yazılır:
√-1 \u003d ± ben .
Benzer akıl yürütme ile, öğrenciler kareleri negatif bir sayıya eşit olan tam iki sayı olduğundan emin olabilirler. ve . Bu sayılar √ ai ve -√ ai . Şartlı olarak, bu şöyle yazılır:
√- bir = ± √ ai .
√ altında bir burada aritmetik yani pozitif kök demek istiyoruz. Örneğin, √4 \u003d 2, √9 \u003d .3; bu nedenle
√-4 = + 2ben , √-9 \u003d ± 3 ben
Daha önce, negatif ayrımcılara sahip kuadratik denklemleri göz önüne alırsak, bu tür denklemlerin kökü olmadığını söyledik, şimdi bunu söylemek mümkün değil. Negatif ayrımcılara sahip ikinci dereceden denklemlerin karmaşık kökleri vardır. Bu kökler bilinen formüllere göre elde edilir. Örneğin, denklemi verelim x 2 + 2x + 5 \u003d 0; sonra
x 1,2 \u003d - 1 ± √1 -5 \u003d - 1 ± √-4 \u003d - 1 ± 2 ben .
Yani, bu denklemin iki kökü var: x 1 = - 1 +2ben , x 2 = - 1 - 2ben . Bu kökler karşılıklı olarak eşleniktir. Tutarlarının - 2 ve ürünün 5 olduğunu, böylece Vieta teoreminin geçerli olduğunu belirtmek ilginçtir.
Karmaşık bir sayı kavramı
Karmaşık bir sayı a + ib formunun bir ifadesidir, burada a ve b herhangi bir gerçek sayıdır, i hayali birim olarak adlandırılan özel bir sayıdır. Bu tür ifadeler için eşitlik kavramları ile toplama ve çarpma işlemleri aşağıdaki gibi tanıtılır:
- İki karmaşık sayı a + ib ve c + id, yalnızca ve yalnızca
a \u003d b ve c \u003d d. - A + ib ve c + id olmak üzere iki karmaşık sayının toplamına karmaşık sayı denir
a + c + i (b + d). - A + ib ve c + id olmak üzere iki karmaşık sayının çarpımı karmaşık sayıdır
ac - bd + i (ad + bc).
Karmaşık sayılar genellikle tek bir harfle gösterilir, örneğin, z \u003d a + ib. Gerçek sayı a, karmaşık sayı z'nin gerçek kısmı olarak adlandırılır, gerçek kısım a \u003d Re z olarak gösterilir. Gerçek sayı b, karmaşık sayı z'nin hayali kısmı olarak adlandırılır, hayali kısım b \u003d Im z ile gösterilir. Bu adlar, karmaşık sayıların aşağıdaki özel özellikleri ile bağlantılı olarak seçilir.
Z \u003d a + i · 0 formunun karmaşık sayıları üzerindeki aritmetik işlemlerin, gerçek sayılarla aynı şekilde gerçekleştirildiğini not ediyoruz. Aslında,
Sonuç olarak, a + i · 0 formunun karmaşık sayıları doğal olarak gerçek sayılarla tanımlanır. Bu nedenle, bu tür karmaşık sayılara basitçe gerçek denir. Yani, gerçek sayılar kümesi karmaşık sayılar kümesinde bulunur. Birçok karmaşık sayı belirtilir. Bunu kurduk, yani
Gerçek sayıların aksine, 0 + ib formundaki sayılara tamamen hayali denir. Genellikle sadece bi yazarlar, örneğin, 0 + i 3 \u003d 3 i. Tamamen hayali sayı i1 \u003d 1 i \u003d i inanılmaz bir özelliğe sahiptir:
Bu şekilde
№ 4 .1. Matematikte sayısal işlev, tanım ve değer alanları sayısal kümelerin alt kümeleri olan bir işlevdir - genellikle gerçek sayılar kümesi veya karmaşık sayılar kümesi.
İşlev grafiği
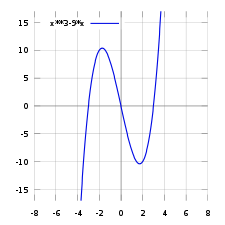
Fonksiyon grafiğinin parçası
İşlev Yolları
[Kaynak] Analitik yöntem
Genellikle bir işlev, değişkenleri, işlemleri ve temel işlevleri içeren bir formül kullanılarak tanımlanır. Belki parçalı bir iş, yani argümanın farklı değerleri için farklı.
[Kaynak] Tablo yolu
Bir işlev, olası tüm bağımsız değişkenlerini ve değerlerini listeleyerek tanımlanabilir. Bundan sonra, gerekirse, enterpolasyon veya ekstrapolasyon ile tabloda bulunmayan argümanlar için işlev yeniden tanımlanabilir. Örnek olarak bir program rehberi, tren tarifesi veya bir Boole işlevi için bir değerler tablosu verilebilir:
[Kaynak] Grafik yolu
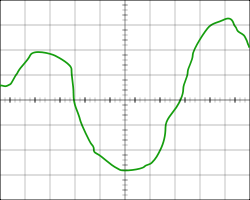
Dalga formu bazı fonksiyonların değerini grafik olarak ayarlar.
İşlev, grafiğinin birçok noktasını düzlemde görüntüleyerek grafiksel olarak ayarlanabilir. Bu, işlevin nasıl görünmesi gerektiği veya cihazdan, örneğin bir osiloskoptan alınan okumaların yaklaşık bir taslağı olabilir. Bu atama yöntemi doğruluk eksikliğinden muzdarip olabilir, ancak bazı durumlarda diğer atama yöntemleri hiç uygulanamaz. Buna ek olarak, fonksiyonların algılanması ve yüksek kaliteli sezgisel analizi için uygun en temsili birini atama yöntemi.
[Kaynak] Özyinelemeli yol
Bir işlev özyineli olarak, yani kendi başına belirtilebilir. Bu durumda, işlevin bazı değerleri diğer değerleri aracılığıyla belirlenir.
- faktöriyel;
- fibonacci sayıları;
- ackerman işlevi.
[Kaynak] Sözlü yol
İşlev, doğal bir dilde kelimelerle, örneğin, girdi ve çıktı değerlerini ya da işlevin bu değerler arasındaki yazışmayı ayarladığı algoritmayı tanımlayarak, herhangi bir açık şekilde tarif edilebilir. Grafiksel yöntemle birlikte, doğal diller biçimsel diller kadar belirleyici olmasa da, bazen bir işlevi tanımlamanın tek yolu budur.
- pi kaydında bir sayıyı numarasına döndüren bir işlev;
- belirli bir zamanda evrendeki atom sayısını döndüren bir işlev;
- bir kişiyi argüman olarak alan ve doğumundan sonra doğacak insan sayısını döndüren bir işlev


