الجذور السالبة للمعادلة التربيعية. كيفية حل المعادلات مع التمييز

التمييز هو مصطلح غامض. هذه المقالة سوف تناقش التمييز من كثير الحدود ، والذي يسمح للشخص لتحديد ما إذا كان متعدد الحدود معين لديه حلول حقيقية. تم العثور على صيغة كثير الحدود مربعة في مسار الجبر والتحليل المدرسي. كيف تجد التمييز؟ ما هو المطلوب لحل المعادلة؟

ويطلق على كثير الحدود مربع أو معادلة من الدرجة الثانية i * w ^ 2 + j * w + k تساوي 0 ، حيث "i" و "j" هما المعاملان الأول والثاني ، على التوالي ، "k" ثابت ، والذي يُطلق عليه أحيانًا "مصطلح حر" ، و "w" متغير. ستكون جذوره هي كل قيم المتغير ، حيث يتحول إلى هوية. من الممكن إعادة كتابة مساواة مثل ناتج i و (w - w1) و (w - w2) يساوي 0. في هذه الحالة ، من الواضح أنه إذا لم يتلاشى المعامل "i" ، فإن الوظيفة على الجانب الأيسر لن تصبح صفرية إلا إذا إذا أخذ x القيمة w1 أو w2. هذه القيم هي نتيجة مساواة كثير الحدود إلى الصفر.

للعثور على قيمة المتغير الذي تختفي فيه الحدود المتعددة الحدود المربعة ، نستخدم بنية مساعدة تستند إلى معاملاتها وتسمى المميِّز. يتم حساب هذا التصميم وفقًا للصيغة D التي تساوي j * j - 4 * i * k. لماذا يتم استخدامه؟

تقول ما إذا كانت هناك نتائج صالحة.
إنها تساعدهم على حساب.

كما توضح هذه القيمة وجود جذور المواد:

إذا كانت موجبة ، فيمكنك العثور على جذرتين في مجال الأعداد الحقيقية.
إذا كان القائم بالتمييز يساوي الصفر ، فإن كلا الحلين يتطابقان. يمكننا أن نقول أن هناك حل واحد فقط ، وهو من مجال الأعداد الحقيقية.
إذا كان المُميّز أقل من الصفر ، فلن يكون لحدود الحدود جذور حقيقية.

خيارات التسوية لإصلاح المواد

للمبلغ (7 * w ^ 2 ؛ 3 * w ؛ 1) يساوي 0 نحسب D بالصيغة 3 * 3 - 4 * 7 * 1 \u003d 9 - 28 نحصل عليها -19. تشير القيمة التمييزية التي تقل عن الصفر إلى عدم وجود نتائج على الخط الحقيقي.

إذا أخذنا في الاعتبار 2 * w ^ 2 - 3 * w + 1 مكافئ 0، ثم يتم حساب D كـ (-3) تربيعًا مطروحًا منه ناتج الأرقام (4 ؛ 2 ؛ 1) ويساوي 9 - 8 ، أي 1. تشير القيمة الموجبة إلى نتيجتين على الخط الحقيقي.

إذا أخذنا المجموع (w ^ 2؛ 2 * w؛ 1) ونساوي 0، يتم حساب D كتربيعين ناقصًا ناتج الأرقام (4 ؛ 1 ؛ 1). سيبسط هذا التعبير إلى 4 - 4 ويختفي. اتضح أن النتائج هي نفسها. إذا نظرت عن كثب إلى هذه الصيغة ، فسيصبح من الواضح أن هذا "مربع كامل". لذلك ، يمكن إعادة كتابة المساواة في النموذج (w + 1) ^ 2 \u003d 0. أصبح من الواضح أن النتيجة في هذه المشكلة هي "-1". في الحالة إذا كانت D تساوي 0 ، فإن الجانب الأيسر من المعادلة سينتهي دائمًا وفقًا لصيغة "المربعة المربعة".

باستخدام التمييز في حساب الجذور

لا يُظهر هذا البناء الإضافي عدد حلول المواد فحسب ، ولكنه يساعد أيضًا في العثور عليها. معادلة الحساب العامة لمعادلة الدرجة الثانية هي كما يلي:

w \u003d (-j +/- d) / (2 * i) ، حيث يمثل d تمييزًا من الدرجة 1/2.

لنفترض أن المُميِّز أقل من الصفر ، ثم d خيالي وأن النتائج وهمية.

D تساوي صفر ، ثم d تساوي D إلى الدرجة 1/2 تساوي أيضًا الصفر. الحل: -j / (2 * i). مرة أخرى ، نعتبر 1 * w ^ 2 + 2 * w + 1 \u003d 0 ، نجد النتائج تعادل -2 / (2 * 1) \u003d -1.

افترض أن D\u003e 0 ، لذلك d عدد حقيقي ، والجواب هنا ينقسمان إلى قسمين: w1 \u003d (-j + d) / (2 * i) و w2 \u003d (-j - d) / (2 * i) . كل النتائج ستكون صالحة. ألق نظرة على 2 * w ^ 2 - 3 * w + 1 \u003d 0. هنا ، وحدات التمييز و d هي وحدات. اتضح أن w1 هي (3 + 1) مقسومة على (2 * 2) أو 1 ، و w2 هي (3 - 1) مقسومة على 2 * 2 أو 1/2.

يتم احتساب نتيجة مساواة التعبير المربع بالصفر وفقًا للخوارزمية:

تحديد عدد القرارات الصحيحة.
حساب د \u003d د ^ (1/2).
العثور على النتيجة وفقًا للصيغة (-j +/- d) / (2 * i).
استبدال النتيجة في المساواة الأصلية للتحقق.

بعض الحالات الخاصة

اعتمادًا على المعاملات ، قد يتم تبسيط الحل إلى حد ما. من الواضح ، إذا كان المعامل أمام المتغير يساوي الصفر إلى الدرجة الثانية ، فيتم الحصول على المساواة الخطية. عندما يكون المعامل قبل المتغير صفراً في الدرجة الأولى ، يكون الخياران ممكنان:

متعدد الحدود يتحول إلى اختلاف في المربعات مع مصطلح حر سلبي ؛
مع ثابت إيجابي ، لا يمكن إيجاد حلول حقيقية.

إذا كان المصطلح الحر هو صفر ، فستكون الجذور (0؛ -j)

ولكن هناك حالات خاصة أخرى تبسط إيجاد حل.

انخفاض المعادلة من الدرجة الثانية

يشار إليها باسم مثل ثلاثي الحدود المربعة ، حيث يكون المعامل أمام المصطلح الأول واحدًا. بالنسبة إلى هذا الموقف ، فإن نظرية فيتا قابلة للتطبيق ، حيث تشير إلى أن مجموع الجذور يساوي معامل المتغير في الدرجة الأولى ، مضروبًا في -1 ، وأن المنتج يتوافق مع الثابت "k".

لذلك ، w1 + w2 تساوي -j و w1 * w2 تساوي k إذا كان المعامل الأول هو واحد. للتحقق من صحة مثل هذا التمثيل ، يمكننا التعبير عن w2 \u003d -j - w1 من الصيغة الأولى واستبدالها في المساواة الثانية w1 * (-j - w1) \u003d k. نتيجة لذلك ، يتم الحصول على المساواة الأولية w1 ^ 2 + j * w1 + k \u003d 0.

المهم أن نلاحظأن i * w ^ 2 + j * w + k \u003d 0 يمكن تخفيضها بقسمة على "i". ستكون النتيجة: w ^ 2 + j1 * w + k1 \u003d 0 ، حيث j1 هي j / i و k1 هي k / i.

ألق نظرة على 2 * w ^ التي تم حلها بالفعل 2 - 3 * w + 1 \u003d 0 مع النتائج w1 \u003d 1 و w2 \u003d 1/2. من الضروري تقسيمها إلى نصفين ، كنتيجة w ^ 2 - 3/2 * w + 1/2 \u003d 0. دعنا نتحقق من أن شروط النظرية صالحة للنتائج التي تم العثور عليها: 1 + 1/2 \u003d 3/2 و 1 * 1/2 \u003d 1 / 2.

حتى المضاعف الثاني

إذا كان عامل المتغير في الدرجة الأولى (ي) قابلاً للقسمة على 2، ثم يمكننا تبسيط الصيغة والبحث عن حل في ربع التمييز D / 4 \u003d (j / 2) ^ 2 - i * k. اتضح w \u003d (-j +/- d / 2) / i ، حيث d / 2 \u003d D / 4 إلى قوة 1/2.

إذا كانت i \u003d 1 ، وكان المعامل j متساويًا ، فإن الحل هو ناتج -1 ونصف المعامل للمتغير w ، زائد / ناقص جذر مربع هذا النصف ناقص الثابت "k". الصيغة: w \u003d -j / 2 +/- (j ^ 2/4 - k) ^ 1/2.

النظام العالي التمييز

يعد تمييز الحالة الثلاثية من الدرجة الثانية المذكورة أعلاه هو الحالة الأكثر استخدامًا. في الحالة العامة ، فإن التمييز بين كثير الحدود هو ضربت مربعات من الاختلافات في جذور هذا كثير الحدود. لذلك ، تشير أداة التمييز التي تساوي الصفر إلى وجود حلين متعددين على الأقل.

فكر في i * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0.

D \u003d j ^ 2 * k ^ 2 - 4 * i * k ^ 3 - 4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

دعنا نقول أن التمييز أكبر من الصفر. هذا يعني أن هناك ثلاثة جذور في مجال الأعداد الحقيقية. في الصفر هناك حلول متعددة. إذا د< 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.

فيديو

سيتحدث فيديونا بالتفصيل عن حساب المُميّز.

لم تحصل على إجابة لسؤالك؟ اقتراح موضوع للمؤلفين.

على سبيل المثال ، بالنسبة للعنصر الثلاثي \\ (3x ^ 2 + 2x-7 \\) ، سيكون المتمايز \\ (2 ^ 2-4 \\ cdot3 \\ cdot (-7) \u003d 4 + 84 \u003d 88 \\). وللثلاثية \\ (x ^ 2-5x + 11 \\) ، سيكون مساوي \\ ((- 5) ^ 2-4 \\ cdot1 \\ cdot11 \u003d 25-44 \u003d -19 \\).

يُشار إلى المُميّز بالحرف \\ (D \\) وغالبًا ما يستخدم في الحل. أيضًا ، حسب قيمة المُميّز ، يمكنك فهم كيف يبدو الرسم البياني تقريبًا (انظر أدناه).

التمييز وجذور المعادلة

تُظهر قيمة المُميِّز عدد المعادلات التربيعية:
   - إذا كانت \\ (D \\) موجبة ، فستكون للمعادلة جذران ؛
   - إذا كان \\ (D \\) يساوي الصفر - جذر واحد فقط ؛
   - إذا كان \\ (D \\) سالبًا ، فلا توجد جذور.

لا تحتاج إلى معرفة ذلك ، فمن السهل التوصل إلى هذا الاستنتاج ، فقط مع العلم أنه من المُميّز (على سبيل المثال ، \\ (\\ sqrt (D) \\) مدرج في الصيغة لحساب جذور المعادلة: \\ (x_ (1) \u003d \\) \\ (\\ .

إذا كان التمييز إيجابيا

في هذه الحالة ، يكون جذرها هو عدد موجب ، مما يعني أن \\ (x_ (1) \\) و \\ (x_ (2) \\) ستكون مختلفة في القيمة ، لأنه في الصيغة الأولى ، تتم إضافة \\ (\\ sqrt (D) \\) ، وفي الثانية - يتم خصمها. ولدينا جذور مختلفة.

مثال : أوجد جذور المعادلة \\ (x ^ 2 + 2x-3 \u003d 0 \\)
قرار :

الجواب : \\ (x_ (1) \u003d 1 \\) ؛ \\ (x_ (2) \u003d - 3 \\)

إذا كان المتميز صفرا

وكم من الجذور سيكون هناك إذا كان التمييز هو صفر؟ دعنا السبب.

تبدو صيغ الجذر كما يلي: \\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) و \\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\). وإذا كان المُميِّز صفراً ، فسيكون جذره أيضًا صفراً. ثم اتضح:

\\ (x_ (1) \u003d \\) \\ (\\ frac (-b + \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b + 0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)

\\ (x_ (2) \u003d \\) \\ (\\ frac (-b- \\ sqrt (D)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b- \\ sqrt (0)) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b-0) (2a) \\) \\ (\u003d \\) \\ (\\ frac (-b) (2a) \\)

أي أن قيم جذور المعادلة ستتزامن ، لأن إضافة أو طرح صفر لا يغير شيئًا.

مثال : أوجد جذور المعادلة \\ (x ^ 2-4x + 4 \u003d 0 \\)
قرار :

\\ (x ^ 2-4x + 4 \u003d 0 \\)		نكتب معاملات:
\\ (a \u003d 1؛ \\) \\ (b \u003d -4؛ \\) \\ (c \u003d 4؛ \\)		نحسب المتمايز بالصيغة \\ (D \u003d b ^ 2-4ac \\)
\\ (D \u003d (- 4) ^ 2-4 \\ cdot1 \\ cdot4 \u003d \\) \(=16-16=0\)		أوجد جذور المعادلة
\\ (x_ (1) \u003d \\) \\ (\\ frac (- (- 4) + \\ sqrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\) \\ (x_ (2) \u003d \\) \\ (\\ frac (- (- 4) - \\ sqrt (0)) (2 \\ cdot1) \\)\\ (\u003d \\) \\ (\\ frac (4) (2) \\) \\ (\u003d 2 \\)		لقد حصلنا على جذرين متطابقين ، لذلك ليس من المنطقي أن نكتبهما بشكل منفصل - نكتب واحدة.

الجواب : \\ (س \u003d 2 \\)

تقول ما إذا كانت هناك نتائج صالحة.
إنها تساعدهم على حساب.

كما توضح هذه القيمة وجود جذور المواد:

إذا كانت موجبة ، فيمكنك العثور على جذرتين في مجال الأعداد الحقيقية.
إذا كان القائم بالتمييز يساوي الصفر ، فإن كلا الحلين يتطابقان. يمكننا أن نقول أن هناك حل واحد فقط ، وهو من مجال الأعداد الحقيقية.
إذا كان المُميّز أقل من الصفر ، فلن يكون لحدود الحدود جذور حقيقية.

خيارات التسوية لإصلاح المواد

باستخدام التمييز في حساب الجذور

w \u003d (-j +/- d) / (2 * i) ، حيث يمثل d تمييزًا من الدرجة 1/2.

لنفترض أن المُميِّز أقل من الصفر ، ثم d خيالي وأن النتائج وهمية.

يتم احتساب نتيجة مساواة التعبير المربع بالصفر وفقًا للخوارزمية:

تحديد عدد القرارات الصحيحة.
حساب د \u003d د ^ (1/2).
العثور على النتيجة وفقًا للصيغة (-j +/- d) / (2 * i).
استبدال النتيجة في المساواة الأصلية للتحقق.

بعض الحالات الخاصة

متعدد الحدود يتحول إلى اختلاف في المربعات مع مصطلح حر سلبي ؛
مع ثابت إيجابي ، لا يمكن إيجاد حلول حقيقية.

إذا كان المصطلح الحر هو صفر ، فستكون الجذور (0؛ -j)

ولكن هناك حالات خاصة أخرى تبسط إيجاد حل.

انخفاض المعادلة من الدرجة الثانية

حتى المضاعف الثاني

النظام العالي التمييز

فكر في i * w ^ 3 + j * w ^ 2 + k * w + m \u003d 0.

D \u003d j ^ 2 * k ^ 2 - 4 * i * k ^ 3 - 4 * i ^ 3 * k - 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

فيديو

سيتحدث فيديونا بالتفصيل عن حساب المُميّز.

لم تحصل على إجابة لسؤالك؟ اقتراح موضوع للمؤلفين.

! المهم في جذور التعددية الزوجية ، لا تغير الوظيفة العلامة.

انتبه! يجب حل أي عدم مساواة غير خطية في مسار الجبر المدرسي باستخدام طريقة الفاصل.

أنا أقدم لكم مفصلة خوارزمية لحل عدم المساواة من خلال طريقة الفاصلبعد ذلك يمكنك تجنب الأخطاء عندما حل عدم المساواة غير الخطية.

حل المعادلات التربيعية مع المميزات السلبية

كما نعلم

أنا 2 = - 1.

في نفس الوقت

(- أنا ) 2 = (- 1 أنا ) 2 = (- 1) 2 أنا 2 = -1.

وبالتالي ، هناك قيمتان على الأقل للجذر التربيعي لـ - 1 ، وهما أنا و - أنا . ولكن ربما هناك بعض الأرقام المعقدة الأخرى التي تساوي مربعاتها - 1؟

لتوضيح هذا السؤال ، افترض مربع الرقم المركب أ + ثنائية يساوي - 1. ثم

(أ + ثنائية ) 2 = - 1,

و 2 + 2أبي - ب 2 = - 1

هناك رقمان معقدان متساويان إذا كانت أجزاؤهما الحقيقية ومعاملات الأجزاء الوهمية متساوية. ول

{	و 2 - ب 2 = - 1 أب = 0 (1)

وفقا للمعادلة الثانية للنظام (1) ، واحد على الأقل من الأرقام و و ب يجب أن يكون الصفر. إذا ب \u003d 0 ، ثم غلة المعادلة الأولى و 2 \u003d - 1. رقم و صالحة وبالتالي و 2 > 0. رقم غير سالب و 2 لا يمكن أن يساوي عدد سالب - 1. لذلك ، فإن المساواة ب \u003d 0 في هذه الحالة مستحيل. يبقى أن يتم الاعتراف بذلك و \u003d 0 ، ولكن بعد المعادلة الأولى للنظام نحصل عليها: - ب 2 = - 1, ب \u003d ± 1.

لذلك ، فإن الأرقام المعقدة التي تكون المربعات فيها -1 هي أرقام فقط أنا و - أنا ، بشروط ، هذا مكتوب كـ:

√-1 \u003d ± أنا .

من خلال التفكير المماثل ، يمكن للطلاب التأكد من وجود رقمين بالضبط تكون المربعات متساوية مع رقم سالب و . هذه الأرقام هي √ منظمة العفو الدولية و -√ منظمة العفو الدولية . بشرط ، هذا هو مكتوب مثل هذا:

√- أ = ± √ منظمة العفو الدولية .

تحت √ ل هنا نعني الحساب ، أي ، الجذر الإيجابي. على سبيل المثال ، √4 \u003d 2 ، √9 \u003d .3 ؛ ول

√-4 = + 2أنا ، √-9 \u003d ± 3 أنا

إذا كان الأمر سابقًا ، عند النظر في المعادلات التربيعية ذات العوامل التمييزية السالبة ، قلنا أن هذه المعادلات ليس لها جذور ، والآن لم يعد من الممكن قول ذلك. المعادلات التربيعية مع التمييز السلبي لها جذور معقدة. يتم الحصول على هذه الجذور وفقا للصيغ المعروفة. اسمحوا ، على سبيل المثال ، أن تعطى المعادلة س 2 + 2س + 5 \u003d 0 ؛ ثم

س 1،2 \u003d - 1 ± √1 -5 \u003d - 1 ± √-4 \u003d - 1 ± 2 أنا .

لذلك ، هذه المعادلة لها جذور: س 1 = - 1 +2أنا , س 2 = - 1 - 2أنا . هذه الجذور متقاربة بشكل متبادل. من المثير للاهتمام أن نلاحظ أن مجموعهم هو - 2 ، والمنتج هو 5 ، بحيث تحمل نظرية فييتا.

مفهوم العدد المركب

الرقم المركب هو تعبير عن النموذج a + ib ، حيث a و b أي أرقام حقيقية ، i هو رقم خاص يسمى وحدة وهمية. بالنسبة لمثل هذه التعبيرات ، يتم تقديم مفاهيم المساواة وعمليات الجمع والضرب على النحو التالي:

يطلق على رقمين معقدين a + ib و c + id متساويين إذا وفقط إذا
أ \u003d ب و ج \u003d د.
يسمى مجموع الرقمين المركبين a + ib و c + id بالرقم المركب
a + c + i (b + d).
نتاج رقمين معقدين a + ib و c + id هو الرقم المركب
ac - bd + i (ad + bc).

غالبًا ما يتم الإشارة إلى الأرقام المركبة بحرف واحد ، على سبيل المثال ، z \u003d a + ib. يُسمى العدد الحقيقي a الجزء الحقيقي من العدد المركب z ، يُشار إلى الجزء الحقيقي a \u003d Re z. يُطلق على العدد الحقيقي b الجزء التخيلي للرقم z المعقّد ، ويُشار إلى الجزء التخيلي ب b \u003d Im z. يتم اختيار هذه الأسماء فيما يتعلق بالخصائص الخاصة التالية للأرقام المركبة.

نلاحظ أن العمليات الحسابية على الأعداد المعقدة من النموذج z \u003d a + i · 0 يتم تنفيذها بنفس الطريقة تمامًا كما في الأعداد الحقيقية. في الواقع،

وبالتالي ، يتم تحديد أرقام معقدة من النموذج a + i · 0 بشكل طبيعي بأرقام حقيقية. ولهذا السبب ، فإن الأرقام المعقدة من هذا النوع تسمى ببساطة حقيقية. لذلك ، مجموعة الأعداد الحقيقية موجودة في مجموعة الأعداد المركبة. يشار إلى العديد من الأرقام المعقدة. لقد أنشأنا ذلك ، أي

على عكس الأرقام الحقيقية ، تُسمى أرقام النموذج 0 + ib وهمية بحتة. في كثير من الأحيان يكتبون ثنائية ، على سبيل المثال ، 0 + i 3 \u003d 3 i. الرقم الخيالي البحت i1 \u003d 1 i \u003d لدي خاصية مذهلة:
بهذه الطريقة

№ 4 .1. في الرياضيات ، الوظيفة العددية هي وظيفة تكون مجالات تعريفها وقيمها عبارة عن مجموعات فرعية من مجموعات رقمية - عادة ما تكون مجموعة من الأرقام الحقيقية أو مجموعة من الأرقام المركبة.

الرسم البياني وظيفة

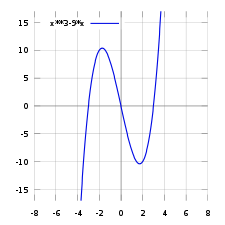
جزء من الرسم البياني وظيفة

طرق لضبط وظيفة

[الاقتباس] الطريقة التحليلية

عادة ، يتم تعريف وظيفة باستخدام صيغة تتضمن المتغيرات والعمليات والوظائف الأولية. ربما تكون وظيفة متقطعة ، أي مختلفة بالنسبة لقيم مختلفة من الوسيطة.

[الاقتباس] طريقة جدولي

يمكن تعريف الوظيفة من خلال سرد جميع الوسائط والقيم الممكنة لها. بعد ذلك ، إذا لزم الأمر ، يمكن إعادة تعريف الوظيفة للوسيطات غير الموجودة في الجدول عن طريق الاستيفاء أو الاستقراء. تتضمن الأمثلة دليل برنامج أو جدول تدريب أو جدول قيم لوظيفة منطقية:

[الاقتباس] طريقة رسومية

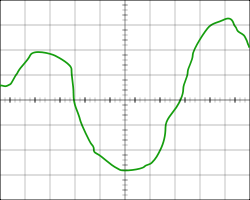
الموجي يحدد قيمة بعض الوظائف بيانيا.

يمكن ضبط الوظيفة بيانيا عن طريق عرض العديد من نقاط الرسم البياني الخاص بها على الطائرة. يمكن أن يكون هذا رسمًا تقريبيًا لما يجب أن تبدو عليه الوظيفة ، أو قراءات مأخوذة من الجهاز ، على سبيل المثال ، من الذبذبات. قد تعاني طريقة التنازل هذه من نقص الدقة ، لكن في بعض الحالات لا يمكن تطبيق طرق أخرى للتخصيص على الإطلاق. بالإضافة إلى ذلك ، هذه الطريقة لتعيين واحدة من الأكثر ملاءمة ، للإدراك وتحليل مجريات الأمور ذات جودة عالية للوظائف.

[الاقتباس] طريقة العودية

يمكن تحديد وظيفة بشكل متكرر ، وهذا هو ، من خلال نفسه. في هذه الحالة ، يتم تحديد بعض قيم الوظيفة من خلال قيمها الأخرى.

مضروب.
أرقام فيبوناتشي
وظيفة أكرمان.

[الاقتباس] الطريقة اللفظية

يمكن وصف الوظيفة بالكلمات بلغة طبيعية بأي طريقة لا لبس فيها ، على سبيل المثال ، عن طريق وصف قيم المدخلات والمخرجات الخاصة بها ، أو الخوارزمية التي تحدد بها الدالة المراسلات بين هذه القيم. جنبا إلى جنب مع الطريقة الرسومية ، في بعض الأحيان هذه هي الطريقة الوحيدة لوصف وظيفة ، على الرغم من أن اللغات الطبيعية ليست حتمية مثل اللغات الرسمية.

دالة تقوم بإرجاع رقم في سجل pi برقمه ؛
دالة تقوم بإرجاع عدد الذرات في الكون في وقت معين من الزمن ؛
وظيفة تأخذ الشخص كحجة وتعيد عدد الأشخاص الذين سوف يولدون بعد ولادته