Funksiya grafigining qiya asimptota tenglamasi shaklga ega. Funksiya grafigining asimptotalarini toping. Shunday qilib, asimptota nima

y \u003d f (x) funktsiyasi grafigining asimptoti to'g'ri chiziq bo'lib, u (x, f (x)) nuqtadan ushbu to'g'ri chiziqgacha bo'lgan masofa cheksiz masofa bilan nolga moyil bo'lgan xususiyatga ega. grafik nuqtasining kelib chiqishi.

3.10-rasm. vertikal, gorizontal va qiya asimptotalarning grafik misollari keltirilgan.

Grafikning asimptotalarini topish quyidagi uchta teoremaga asoslanadi.

Vertikal asimptota teoremasi. y \u003d f (x) funktsiyasi x 0 nuqtasining ba'zi qo'shnilarida aniqlansin (ehtimol bu nuqtaning o'zi bundan mustasno) va funktsiyaning bir tomonlama chegaralaridan kamida bittasi cheksizlikka teng bo'lsin, ya'ni. Keyin x \u003d x 0 chizig'i y \u003d f (x) funktsiyasi grafigining vertikal asimptotidir.

Shubhasiz, agar funktsiya x 0 nuqtasida uzluksiz bo'lsa, x \u003d x 0 chizig'i vertikal asimptota bo'la olmaydi, chunki bu holda . Shuning uchun vertikal asimptotalarni funksiyaning uzilish nuqtalarida yoki uning sohasi uchlarida izlash kerak.

Gorizontal asimptota haqidagi teorema. y \u003d f (x) funktsiyasi etarlicha katta x uchun aniqlansin va funktsiyaning chekli chegarasi bo'lsin. U holda y = b chiziq funksiya grafigining gorizontal asimptotasidir.

Izoh. Agar chegaralardan faqat bittasi chekli bo'lsa, u holda funksiya mos ravishda chap yoki o'ng gorizontal asimptotaga ega bo'ladi.

Bunday holda, funktsiya qiya asimptotaga ega bo'lishi mumkin.

Oblik asimptota teoremasi. Yetarli darajada katta x uchun y = f(x) funksiya aniqlansin va chekli chegaralar bo‘lsin . U holda y = kx + b chiziq funksiya grafigining qiya asimptotasidir.

Dalilsiz.

Mos keladigan chegaralarning asosi ma'lum bir belgining cheksizligi bo'lsa, qiya asimptota, shuningdek, gorizontal, o'ng yoki chap qo'l bo'lishi mumkin.

Funktsiyalarni o'rganish va ularning grafiklarini qurish odatda quyidagi bosqichlarni o'z ichiga oladi:

1. Funksiya sohasini toping.

2. Juft-toq uchun funksiyani o‘rganing.

3. Agar ular chekli bo'lsa, uzilish nuqtalari va funksiyaning aniqlanish sohasi chegaralaridagi xatti-harakatlarini o'rganib, vertikal asimptotalarni toping.

4. Funksiyaning cheksizlikdagi harakatini tekshirib, gorizontal yoki qiya asimptotalarni toping.

5. Funksiyaning monotonligining ekstremal va intervallarini toping.

6. Funksiyaning qavariq oraliqlarini va burilish nuqtalarini toping.

7. Koordinata o'qlari bilan kesishish nuqtalarini va, ehtimol, grafikni aniqlaydigan ba'zi qo'shimcha nuqtalarni toping.

Funktsional differentsial

Isbotlash mumkinki, agar funktsiya ma'lum bir asos uchun chekli songa teng chegaraga ega bo'lsa, u holda uni shu sonning yig'indisi va bir xil asos uchun cheksiz kichik qiymat sifatida ko'rsatish mumkin (va aksincha): .

Bu teoremani differensiallanuvchi funksiyaga tadbiq qilaylik: .

Shunday qilib, Dy funksiyaning o'sishi ikki haddan iborat: 1) Dx ga nisbatan chiziqli, ya'ni. f`(x)Dx; 2) Dx ga nisbatan chiziqli bo'lmagan, ya'ni. a(Dx)Dx. Shu bilan birga, beri , bu ikkinchi had Dx ga qaraganda yuqori tartibli cheksiz kichikdir (Dx nolga intilayotgani uchun u tezroq nolga intiladi).

Funksiya differensiali funktsiya o'sishning Dx ga nisbatan bosh, chiziqli qismi bo'lib, hosila va mustaqil o'zgaruvchining dy = f `(x)Dx ko'paytmasiga teng.

y = x funksiyaning differentsialini toping.

Chunki dy = f `(x)Dx = x`Dx = Dx, keyin dx = Dx, ya'ni. mustaqil o'zgaruvchining differensialligi shu o'zgaruvchining o'sishiga teng.

Demak, funktsiyani differentsiallash formulasini dy = f `(x)dx shaklida yozish mumkin. Shuning uchun hosila belgilaridan biri dy/dx kasrdir.

Differensialning geometrik ma'nosi tasvirlangan
3.11-rasm. y = f(x) funksiya grafigida ixtiyoriy M(x, y) nuqtani oling. X argumentiga Dx ortishini beraylik. Shunda y = f(x) funksiya Dy = f(x + Dx) - f(x) ortishini oladi. Funktsiya grafigiga M nuqtada teginish chizamiz, u x o'qining musbat yo'nalishi bilan a burchak hosil qiladi, ya'ni. f `(x) = tg a. MKN to'g'ri burchakli uchburchakdan
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy.

Demak, funktsiyaning differensialligi x Dx ga oshirilganda berilgan nuqtada funksiya grafigiga chizilgan tangens ordinatasidagi o'sishdir.

Differensialning xossalari asosan hosilalarning xossalari bilan bir xil:

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v 2 .

Biroq, funktsiya differentsialining uning hosilasida mavjud bo'lmagan muhim xususiyati mavjud - bu differentsial shaklining o'zgarmasligi.

y = f(x) funksiya uchun differentsial ta’rifidan dy = f`(x)dx differensial hisoblanadi. Agar bu funktsiya y murakkab bo'lsa, ya'ni. y = f(u), bu erda u = j(x), keyin y = f va f `(x) = f `(u)*u`. Keyin dy = f`(u)*u`dx. Ammo funktsiya uchun
u = j(x) differensial du = u`dx. Demak, dy = f `(u)*du.

dy = f `(x)dx va dy = f `(u)*du tengliklarini taqqoslab, agar mustaqil o'zgaruvchining funktsiyasi o'rniga x funktsiyasini ko'rib chiqsak, differentsial formula o'zgarmasligiga ishonch hosil qilamiz. qaram o'zgaruvchi u. Differensialning bu xossasi differentsial shaklining (yoki formulasining) o'zgarmasligi (ya'ni o'zgarmasligi) deb ataladi.

Biroq, bu ikki formulada hali ham farq mavjud: ularning birinchisida mustaqil o'zgaruvchining differentsiali bu o'zgaruvchining o'sishiga teng, ya'ni. dx = Dx, ikkinchisida esa du funksiyasining differensialligi bu funksiya Du ortishining faqat chiziqli qismidir va faqat kichik Dx du » Du uchun.

Oddiy vazifa shunday tuzilgan va u grafikning HAMMA asimptotalarini (vertikal, qiya / gorizontal) topishni o'z ichiga oladi. Garchi, savolni shakllantirishda aniqroq bo'lsa-da, biz asimptotalarning mavjudligini o'rganish haqida gapiramiz (oxir-oqibat, umuman bo'lmasligi mumkin).

Keling, oddiy narsadan boshlaylik:

1-misol

Yechimni qulay tarzda ikki qismga bo'lish mumkin:

1) Avval vertikal asimptotlar mavjudligini tekshiramiz. Maxraj da yo'qoladi va shu nuqtada funktsiya cheksiz uzilishga duchor bo'lishi darhol aniq bo'ladi va tenglama tomonidan berilgan to'g'ri chiziq funktsiya grafigining vertikal asimptotu hisoblanadi. Ammo bunday xulosa chiqarishdan oldin, bir tomonlama chegaralarni topish kerak:

Men xuddi shunday funktsiyaning uzluksizligi haqidagi maqolada to'xtalgan hisoblash texnikasini eslayman. tanaffus nuqtalari. Chegara belgisi ostidagi ifodada "x" o'rniga biz ni almashtiramiz. Numeratorda qiziq narsa yo'q:
.

Ammo denominatorda bu chiqadi cheksiz kichik manfiy son:
, u chegaraning taqdirini belgilaydi.

Chap qo'l chegarasi cheksizdir va, qoida tariqasida, vertikal asimptota mavjudligi to'g'risida allaqachon hukm chiqarish mumkin. Ammo bir tomonlama chegaralar nafaqat buning uchun kerak - ular SIZGA funktsiya grafigi QANDAY joylashganligini va uni TO'G'ri qurishga yordam beradi. Shuning uchun biz o'ng chegarani ham hisoblashimiz kerak:

Xulosa: bir tomonlama chegaralar cheksizdir, bu chiziq funksiya grafigining vertikal asimptoti ekanligini bildiradi.

Birinchi chegara cheklangan, bu "suhbatni davom ettirish" va ikkinchi chegarani topish kerakligini anglatadi:

Ikkinchi chegara ham cheklangan.

Shunday qilib, bizning asimptotimiz:

Xulosa: tenglama bilan berilgan to'g'ri chiziq funksiya grafigining gorizontal asimptotasidir.

Gorizontal asimptotani topish uchun siz soddalashtirilgan formuladan foydalanishingiz mumkin:

Agar chekli chegara mavjud bo'lsa, u holda chiziq funktsiya grafigining gorizontal asimptotasidir.

Funktsiyaning numeratori va maxraji bir xil o'sish tartibida ekanligini ko'rish oson, ya'ni kerakli chegara chekli bo'ladi:

Javob:

Shartga ko'ra, chizmani bajarish shart emas, lekin agar funktsiyani o'rganish qizg'in davom etsa, biz darhol qoralama chizmasini tuzamiz:

Topilgan uchta chegaraga asoslanib, funktsiya grafigini qanday joylashtirish mumkinligini mustaqil ravishda aniqlashga harakat qiling. Juda qiyinmi? 5-6-7-8 nuqtalarni toping va ularni chizmaga belgilang. Biroq, bu funktsiyaning grafigi elementar funksiya grafigini o'zgartirishlar yordamida qurilgan va ushbu maqolaning 21-misolini sinchkovlik bilan ko'rib chiqqan o'quvchilar uning qanday egri chiziq ekanligini osongina taxmin qilishlari mumkin.

2-misol

Funksiya grafigining asimptotalarini toping

Bu o'z-o'zidan bajariladigan misol. Men sizga eslatib o'taman, jarayon qulay tarzda ikki nuqtaga bo'linadi - vertikal asimptota va qiya asimptota. Namuna yechimida gorizontal asimptota soddalashtirilgan sxema yordamida topiladi.

Amalda kasr-ratsional funktsiyalar ko'pincha uchraydi va giperbolalar bo'yicha mashg'ulotlardan so'ng biz vazifani murakkablashtiramiz:

3-misol

Funksiya grafigining asimptotalarini toping

Yechim: Bir, ikkita va bajarildi:

1) Vertikal asimptotlar cheksiz uzilish nuqtalarida, shuning uchun siz maxrajning yo'qolishini tekshirishingiz kerak. Kvadrat tenglamani yechamiz:

Diskriminant musbat, shuning uchun tenglama ikkita haqiqiy ildizga ega va ish sezilarli darajada qo'shiladi =)

Bir tomonlama chegaralarni topish uchun kvadrat trinomialni faktorlarga ajratish qulay:
(ixcham yozuv uchun "minus" birinchi qavsga kiritilgan). Xavfsizlik tarmog'i uchun biz qavslarni ochib, aqliy yoki qoralama bo'yicha tekshirishni amalga oshiramiz.

Funksiyani formada qayta yozamiz

Nuqtada bir tomonlama chegaralarni toping:

Va shu nuqtada:

Shunday qilib, to'g'ri chiziqlar ko'rib chiqilayotgan funksiya grafigining vertikal asimptotalari hisoblanadi.

2) Agar funktsiyaga qarasangiz, chegara chekli bo'lishi aniq va bizda gorizontal asimptota mavjud. Keling, buni qisqacha ko'rsatamiz:

Shunday qilib, to'g'ri chiziq (abtsissa) bu funktsiya grafigining gorizontal asimptotasidir.

Javob:

Topilgan chegaralar va asimptotlar funksiya grafigi haqida juda ko'p ma'lumot beradi. Quyidagi faktlarni hisobga olgan holda rasmni aqliy tasavvur qilishga harakat qiling:

Grafikning o'z versiyasini qoralamaga chizing.

Albatta, topilgan chegaralar grafik turini aniq belgilamaydi va siz xato qilishingiz mumkin, ammo mashqning o'zi funktsiyani to'liq o'rganish jarayonida bebaho yordam beradi. To'g'ri rasm dars oxirida.

4-misol

Funksiya grafigining asimptotalarini toping

5-misol

Funksiya grafigining asimptotalarini toping

Bu mustaqil qaror qabul qilish uchun vazifalar. Ikkala grafikda ham yana gorizontal asimptotalar mavjud bo‘lib, ular darhol quyidagi xususiyatlar bilan aniqlanadi: 4-misolda maxrajning o‘sish tartibi hisobning o‘sish tartibidan kattaroq, 5-misolda esa pay va maxraj bir xil tartibda. o'sish. Namuna yechimida birinchi funktsiya qiya asimptotalarning mavjudligi uchun to'liq, ikkinchisi - chegara orqali tekshiriladi.

Gorizontal asimptotlar, mening sub'ektiv taassurotimga ko'ra, "haqiqatan ham egilgan" ga qaraganda sezilarli darajada keng tarqalgan. Uzoq kutilgan umumiy holat:

6-misol

Funksiya grafigining asimptotalarini toping

Yechim: janr klassikasi:

1) maxraj musbat bo‘lgani uchun funksiya butun son chizig‘ida uzluksiz bo‘lib, vertikal asimptotlar yo‘q. …Bu yaxshimi? To'g'ri so'z emas - ajoyib! №1 band yopiq.

2) qiya asimptotalarning mavjudligini tekshiring:

Birinchi chegara cheklangan, keling, davom etaylik. "Cheksizlik minus cheksizlik" noaniqligini bartaraf etish uchun ikkinchi chegarani hisoblash jarayonida biz ifodani umumiy maxrajga qisqartiramiz:

Ikkinchi chegara ham cheklangan, shuning uchun ko'rib chiqilayotgan funksiya grafigi qiya asimptotaga ega:

Xulosa:

Shunday qilib, funktsiya grafigi uchun cheksiz yaqin to'g'ri chiziqqa yaqinlashadi:

E'tibor bering, u o'zining qiya asimptotasini boshidan kesib o'tadi va bunday kesishish nuqtalari juda maqbuldir - cheksizlikda "hamma narsa normal" bo'lishi muhim (aslida, asimptotalarning muhokamasi o'sha erda paydo bo'ladi).

7-misol

Funksiya grafigining asimptotalarini toping

Qaror: izoh beradigan hech narsa yo'q, shuning uchun men yakuniy yechimning taxminiy namunasini tuzaman:

1) Vertikal asimptotlar. Keling, nuqtani o'rganamiz.

To'g'ri chiziq - da uchastkaning vertikal asimptotasi.

2) qiyshiq asimptotlar:

To'g'ri chiziq - dagi grafik uchun qiya asimptota.

Javob:

Topilgan bir tomonlama chegaralar va asimptotalar ushbu funktsiya grafigi qanday ko'rinishini yuqori aniqlik bilan taxmin qilish imkonini beradi. Dars oxirida to'g'ri chizish.

8-misol

Funksiya grafigining asimptotalarini toping

Bu mustaqil yechim uchun misoldir, ba'zi chegaralarni hisoblash qulayligi uchun siz hisoblagichni maxraj atamasi bo'yicha muddatga bo'lishingiz mumkin. Va yana, natijalarni tahlil qilib, ushbu funktsiyaning grafigini chizishga harakat qiling.

Shubhasiz, "haqiqiy" qiya asimptotalarning egalari hisoblagichning eng yuqori darajasi maxrajning eng yuqori darajasidan bir kattaroq bo'lgan kasr-ratsional funktsiyalarning grafiklaridir. Agar ko'proq bo'lsa, qiya asimptota bo'lmaydi (masalan, ).

Ammo hayotda boshqa mo''jizalar sodir bo'ladi:

9-misol

Yechish: funksiya butun son qatorida uzluksiz, ya’ni vertikal asimptotlar yo‘q. Ammo qiyaliklar bo'lishi mumkin. Biz tekshiramiz:

Universitetda shunga o'xshash funktsiyaga qanday duch kelganimni eslayman va uning qiya asimptotaga ega ekanligiga ishonolmadim. Ikkinchi chegarani hisoblamagunimcha:

To'g'ri aytganda, bu erda ikkita noaniqlik mavjud: va , lekin u yoki bu tarzda, murakkablik chegaralarini oshirish bo'yicha maqolaning 5-6-misollarida muhokama qilingan yechim usulidan foydalanishingiz kerak. Formuladan foydalanish uchun konjugat ifodaga ko'paytiring va bo'ling:

Javob:

Ehtimol, eng mashhur oblique asimptote.

Hozirgacha cheksizlik "bir xil cho'tka bilan kesilgan", ammo funksiya grafigida ikkita turli xil qiya asimptotlar mavjud:

10-misol

Asimptotlar uchun funksiya grafigini ko‘rib chiqing

Qaror: radikal ifoda ijobiy, ya'ni ta'rif sohasi har qanday haqiqiy son bo'lib, vertikal tayoqchalar bo'lishi mumkin emas.

Keling, qiya asimptotlar mavjudligini tekshiramiz.

Agar "x" "minus cheksizlik" ga moyil bo'lsa, unda:
(kvadrat ildiz ostida "x" ni kiritishda salbiy maxrajni yo'qotmaslik uchun "minus" belgisini qo'shishingiz kerak)

Bu g'ayrioddiy ko'rinadi, lekin bu erda noaniqlik "cheksizlik minus cheksizlik" dir. Numerator va maxrajni qo‘shma iboraga ko‘paytiring:

Shunday qilib, to'g'ri chiziq - da grafikning qiya asimptotu.

"Plyus cheksizlik" bilan hamma narsa ahamiyatsizroq:

Va to'g'ri chiziq - at .

Javob:

Agar ;
, Agar .

Men grafik tasvirga qarshi tura olmayman:

Bu giperbolaning tarmoqlaridan biridir.

Asimptotalarning potentsial mavjudligi dastlab funktsiya sohasi bilan cheklanishi odatiy hol emas:

11-misol

Asimptotlar uchun funksiya grafigini ko‘rib chiqing

Yechish: ko'rinib turibdiki, shuning uchun biz faqat o'ng yarim tekislikni ko'rib chiqamiz, bu erda funktsiya grafigi mavjud.

1) Funksiya intervalda uzluksizdir, ya’ni vertikal asimptota mavjud bo‘lsa, u faqat y o‘qi bo‘lishi mumkin. Biz nuqta yaqinidagi funktsiyaning harakatini o'rganamiz o'ngda:

E'tibor bering, bu erda noaniqlik yo'q (e'tibor "Limitlarni hal qilish usullari" maqolasining boshida bunday holatlarga qaratilgan).

Shunday qilib, to'g'ri chiziq (y o'qi) funksiya grafigi uchun vertikal asimptota hisoblanadi.

2) Qiyma asimptotani o'rganish to'liq amalga oshirilishi mumkin, ammo L'Hopital qoidalari maqolasida biz logarifmikdan yuqori o'sish tartibidagi chiziqli funktsiya ekanligini aniqladik, shuning uchun: (1-misolga qarang). xuddi shu dars).

Xulosa: abscissa o'qi funksiya grafigining gorizontal asimptotasidir.

Javob:

Agar ;
, Agar .

Aniqlik uchun chizish:

Qizig'i shundaki, ko'rinishidan o'xshash funktsiyaning asimptotalari umuman yo'q (xohlaganlar buni tekshirishlari mumkin).

Ikki yakuniy o'z-o'zini o'rganish misollari:

12-misol

Asimptotlar uchun funksiya grafigini ko‘rib chiqing

Vertikal asimptotalarni tekshirish uchun birinchi navbatda funktsiyaning domenini topishingiz kerak, so'ngra "shubhali" nuqtalarda bir tomonlama chegaralar juftligini hisoblang. Oblik asimptotlar ham bundan mustasno emas, chunki funktsiya "ortiqcha" va "minus" cheksizlik bilan belgilanadi.

13-misol

Asimptotlar uchun funksiya grafigini ko‘rib chiqing

Va bu erda faqat oblik asimptotlar bo'lishi mumkin va yo'nalishlar , alohida ko'rib chiqilishi kerak.

Umid qilamanki, siz to'g'ri asimptotni topdingiz =)

Omad tilayman!

Yechimlar va javoblar:

2-misol:Yechim :
. Keling, bir tomonlama chegaralarni topaylik:

Streyt da funksiya grafigining vertikal asimptotasidir .
2) qiya asimptotlar.

Streyt .
Javob:

Chizma3-misolga:

4-misol:Yechim :
1) Vertikal asimptotlar. Funktsiya bir nuqtada cheksiz tanaffusga duchor bo'ladi . Keling, bir tomonlama chegaralarni hisoblaylik:

Eslatma: Juft darajali cheksiz kichik manfiy son cheksiz kichik musbat songa teng: .

Streyt funksiya grafigining vertikal asimptotasidir.
2) qiya asimptotlar.

Streyt (abscissa) funksiya grafigining gorizontal asimptotasi .
Javob: . .
Shunday qilib, da grafikda qiya asimptota yo'q.

Shunday qilib, to'g'ridan-to'g'ri da bu funksiya grafigining gorizontal asimptoti .
Javob: abscissa da .

Sirtqi talabalar uchun oliy matematika va nafaqat >>>

(Asosiy sahifaga o'tish)

Funktsiya null. Funktsiyaning doimiylik intervallari.

Bo'shliq usuli

Losmalar va funktsiyalarni o'rganish bilan bog'liq materiallarning aksariyati an'anaviy ravishda maktab o'quv dasturiga tegishli va ushbu maqola qoidadan istisno emas. Bugun biz funktsiyaning nollarini va doimiy ishorali intervallarini topishni mashq qilamiz, shuningdek, ko'rib chiqilayotgan mavzu devorlarida ishonchli mustahkamlash bilan taqqoslanadigan intervallar usulini batafsil tahlil qilamiz.

Agar sizning bino loyihangiz qazish bosqichida bo'lsa, iltimos, xususiyatlar grafiklari bo'yicha kirish darsidan boshlang. Bundan tashqari, “Funksiyani aniqlash sohasi”, “Grafik asimptotlari” maqolalari bilan tanishib chiqish tavsiya etiladi va mohiyatan ushbu sahifadagi ma’lumotlar mantiqiy davomidir. Material, albatta, o'rta maktab o'quvchilari uchun foydali bo'ladi.

2020-yil iyul oyida NASA Marsga ekspeditsiyani boshlaydi. Koinot kemasi Marsga ekspeditsiyaning barcha ro‘yxatdan o‘tgan a’zolarining ismlari yozilgan elektron tashuvchini yetkazadi.

Ishtirokchilarni ro'yxatga olish ochiq. Marsga chiptani ushbu havola orqali oling.

Agar ushbu post muammoingizni hal qilgan bo'lsa yoki sizga shunchaki yoqqan bo'lsa, unga havolani ijtimoiy tarmoqlardagi do'stlaringiz bilan baham ko'ring.

Ushbu kod variantlaridan birini nusxalash va veb-sahifa kodingizga joylashtirish kerak, yaxshisi teglar orasiga yoki tegdan keyin. Birinchi variantga ko'ra, MathJax tezroq yuklanadi va sahifani kamroq sekinlashtiradi. Ammo ikkinchi variant MathJax-ning so'nggi versiyalarini avtomatik ravishda kuzatib boradi va yuklaydi. Agar siz birinchi kodni kiritsangiz, uni vaqti-vaqti bilan yangilab turish kerak bo'ladi. Agar siz ikkinchi kodni joylashtirsangiz, sahifalar sekinroq yuklanadi, lekin siz MathJax yangilanishlarini doimiy ravishda kuzatib borishingiz shart emas.

MathJax-ni ulashning eng oson yo'li Blogger yoki WordPress-da: saytni boshqarish paneliga uchinchi tomon JavaScript kodini kiritish uchun mo'ljallangan vidjetni qo'shing, unga yuqoridagi yuklash kodining birinchi yoki ikkinchi versiyasini nusxalang va vidjetni yaqinroq joylashtiring. shablonning boshlanishi (Aytgancha, bu umuman kerak emas, chunki MathJax skripti asinxron ravishda yuklangan). Ana xolos. Endi MathML, LaTeX va ASCIIMathML belgilash sintaksisini o'rganing va siz matematik formulalarni veb-sahifalaringizga joylashtirishga tayyorsiz.

Yana bir yangi yil kechasi... sovuq ob-havo va deraza oynasidagi qor parchalari... Bularning barchasi meni yana... fraktallar va Volfram Alfa bu haqda nima bilishi haqida yozishga undadi. Shu munosabat bilan qiziqarli maqola bor, unda ikki o'lchovli fraktal tuzilmalarning misollari mavjud. Bu erda biz uch o'lchamli fraktallarning yanada murakkab misollarini ko'rib chiqamiz.

Fraktalni geometrik shakl yoki jism sifatida ko'rish (ta'riflash) mumkin (ya'ni ikkalasi ham to'plam, bu holda nuqtalar to'plami), uning tafsilotlari asl figuraning o'zi bilan bir xil shaklga ega. Ya'ni, bu o'ziga o'xshash tuzilma bo'lib, uning tafsilotlarini hisobga olsak, kattalashtirilganda, biz kattalashtirmasdan bir xil shaklni ko'ramiz. Oddiy geometrik figuraga (fraktal emas) kelsak, kattalashganda, biz asl figuraning o'zidan oddiyroq shaklga ega bo'lgan tafsilotlarni ko'ramiz. Masalan, etarlicha yuqori kattalashtirishda ellipsning bir qismi to'g'ri chiziq segmentiga o'xshaydi. Fraktallar bilan bu sodir bo'lmaydi: ulardagi har qanday o'sish bilan biz yana bir xil murakkab shaklni ko'ramiz, bu har bir o'sish bilan yana va yana takrorlanadi.

Fraktallar fanining asoschisi Benua Mandelbrot o'zining "Fraktallar va fan uchun san'at" maqolasida shunday yozgan edi: "Fraktallar umumiy shaklida bo'lgani kabi o'zlarining tafsilotlari jihatidan ham murakkab geometrik shakllardir. Ya'ni fraktal irodaning bir qismi bo'lsa. butunning o'lchamiga kattalashtirilsa, u butunga o'xshaydi, yoki aniq yoki ehtimol biroz deformatsiya bilan ko'rinadi.

Ta'rif. Funksiya grafigining asimptoti - bu funktsiya grafigi nuqtasidan ushbu chiziqgacha bo'lgan masofa grafik nuqtasining boshidan cheksiz masofada nolga moyil bo'lgan xususiyatga ega bo'lgan chiziq..

Ularni topish usullariga ko'ra asimptotalarning uch turi ajratiladi: vertikal, gorizontal, qiya.

Shubhasiz, gorizontallar moyil bo'lganlarning maxsus holatlaridir (uchun).

Funksiya grafigining asimptotalarini topish quyidagi gaplarga asoslanadi.

Teorema 1. Funktsiya hech bo'lmaganda nuqtaning qandaydir yarim qo'shnisida aniqlansin va uning bir tomonlama chegaralaridan hech bo'lmaganda bittasi bu nuqtada cheksiz bo'lsin, ya'ni. teng. U holda to‘g‘ri chiziq funksiya grafigining vertikal asimptoti bo‘ladi.

Shunday qilib, funktsiya grafigining vertikal asimptotalarini funktsiyaning uzilish nuqtalarida yoki uning ta'rif sohasi oxirida (agar bu chekli sonlar bo'lsa) izlash kerak.

Teorema 2. Funktsiya mutlaq qiymatda etarlicha katta bo'lgan va funktsiyaning chekli chegarasi mavjud bo'lgan argument qiymatlari uchun aniqlansin. . U holda chiziq funktsiya grafigining gorizontal asimptoti bo'ladi.

Shunday bo'lishi mumkin , A , va chekli sonlar bo‘lsa, grafik ikki xil gorizontal asimptotaga ega: chap va o‘ng qo‘l. Agar chekli chegaralardan faqat bittasi yoki mavjud bo'lsa, u holda grafik bitta chap qo'l yoki bitta o'ng qo'l gorizontal asimptotaga ega.

Teorema 3. Funktsiya mutlaq qiymatda etarlicha katta bo'lgan va cheklangan chegaralar mavjud bo'lgan argument qiymatlari uchun aniqlansin. Va . U holda to'g'ri chiziq funksiya grafigining qiya asimptotasidir.

E'tibor bering, agar ushbu chegaralardan kamida bittasi cheksiz bo'lsa, unda hech qanday qiyshiq asimptota yo'q.

Egri asimptota, gorizontal kabi, bir tomonlama bo'lishi mumkin.

Misol. Funksiya grafigining barcha asimptotalarini toping.

Yechim.

Funktsiya bilan aniqlanadi. Uning nuqtalardagi bir tomonlama chegaralarini topamiz.

Chunki Va (boshqa ikkita bir tomonlama chegaralar endi topilmaydi), u holda chiziqlar funksiya grafigining vertikal asimptotalari hisoblanadi.

Hisoblash

(L'Hopital qoidasini qo'llang) = .

Demak, chiziq gorizontal asimptotadir.

Gorizontal asimptota mavjud bo'lgani uchun biz endi qiya asimptotalarni qidirmaymiz (ular yo'q).

Javob: Grafikda ikkita vertikal va bitta gorizontal asimptota mavjud.

Umumiy funktsiyani o'rganish y = f(x).

Funktsiya doirasi. Uning domenini toping D(f). Agar bu juda qiyin bo'lmasa, diapazonni ham topish foydali bo'ladi E(f). (Biroq, ko'p hollarda, topish masalasi E(f) funksiyaning ekstremal qismi topilguncha kechiktiriladi.)

Funksiyaning maxsus xossalari. Funksiyaning umumiy xossalarini aniqlang: juft, toq, davriylik va boshqalar. Har bir funktsiya juft yoki toq kabi xususiyatlarga ega emas. Agar funktsiyaning aniqlanish sohasi o'qdagi 0 nuqtaga nisbatan assimetrik bo'lsa, albatta, u ham, na toq emas. ho'kiz. Xuddi shu tarzda, har qanday davriy funktsiya uchun ta'rif sohasi butun haqiqiy o'qdan yoki davriy takrorlanadigan intervallar tizimlarining birlashmasidan iborat.

Vertikal asimptotlar. Argument aniqlanish sohasining chegara nuqtalariga yaqinlashganda funktsiya qanday harakat qilishini aniqlang D(f) agar shunday chegara nuqtalari mavjud bo'lsa. Bunday holda, vertikal asimptotlar paydo bo'lishi mumkin. Agar funktsiya aniqlanmagan shunday uzilish nuqtalariga ega bo'lsa, u holda bu nuqtalar funksiyaning vertikal asimptotalari mavjudligi uchun ham tekshiriladi.

Egri va gorizontal asimptotlar. Agar ko'lami D(f) (a;+) yoki (-;b) koʻrinishdagi nurlarni oʻz ichiga oladi, keyin mos ravishda x+ yoki x− da qiya asimptotalarni (yoki gorizontal asimptotalarni) topishga harakat qilishimiz mumkin, yaʼni. limxf(x) ni toping. Egri asimptotlar: y = kx + b, Bu yerda k=limx+xf(x) va b=limx+(f(x)−x). Gorizontal asimptotlar: y = b, bu yerda limxf(x)=b.

Grafikning o'qlar bilan kesishish nuqtalarini topish. Grafikning o'q bilan kesishish nuqtasini topish Oy. Buning uchun siz qiymatni hisoblashingiz kerak f(0). Grafikning o'q bilan kesishish nuqtalarini ham toping ho'kiz, nima uchun tenglamaning ildizlarini toping f(x) = 0 (yoki ildizlar yo'qligiga ishonch hosil qiling). Ko'pincha tenglamani faqat taxminan echish mumkin, ammo ildizlarni ajratish grafik tuzilishini yaxshiroq tushunishga yordam beradi. Keyinchalik, funktsiya belgisini ildizlar va sinish nuqtalari orasidagi intervallarda aniqlashingiz kerak.

Grafikning asimptota bilan kesishish nuqtalarini topish. Ba'zi hollarda, oldingi paragraflarda aytilmagan grafikning xarakterli nuqtalarini topish kerak bo'lishi mumkin. Masalan, agar funktsiya qiya asimptotaga ega bo'lsa, u holda grafikning ushbu asimptota bilan kesishgan nuqtalari mavjudligini aniqlashga harakat qilishingiz mumkin.

Qavariq va botiqlik intervallarini topish. Bu f(x) ning ikkinchi hosilasining belgisini tekshirish orqali amalga oshiriladi. Qavariq va botiq oraliqlarning tutashgan joylaridagi burilish nuqtalarini toping. Funksiyaning burilish nuqtalaridagi qiymatini hisoblang. Agar funktsiyaning ikkinchi hosilasi 0 ga teng bo'lgan yoki mavjud bo'lmagan boshqa uzluksizlik nuqtalari bo'lsa (burilish nuqtalaridan tashqari), u holda bu nuqtalarda funktsiya qiymatini hisoblash ham foydalidir. f(x) ni topib, f(x)0 tengsizlikni yechamiz. Eritma oraliqlarining har birida funktsiya pastga qarab qavariq bo'ladi. Teskari f(x)0 tengsizlikni yechib, funksiya yuqoriga (ya’ni botiq) qavariq bo‘lgan oraliqlarni topamiz. Biz burilish nuqtalarini funktsiya qavariqlik yo'nalishini o'zgartiradigan (va uzluksiz) nuqtalar deb belgilaymiz.

Funksiya grafigining asimptotalari

Asimptota sharpasi uzoq vaqt davomida sayt bo'ylab kezib yuribdi va nihoyat bitta maqolada paydo bo'ldi va funktsiyani to'liq o'rganishdan hayratda qolgan o'quvchilarni quvontirdi. Grafikning asimptotalarini topish ko'rsatilgan vazifaning bir nechta qismlaridan biri bo'lib, u maktab kursida faqat umumiy ko'rib chiqish tartibida yoritiladi, chunki voqealar funktsiyalar chegaralarini hisoblash atrofida aylanadi va ular hali ham oliy matematikaga tegishli. . Matematik tahlilni yaxshi bilmaydigan mehmonlar, menimcha, maslahat tushunarli ;-) ... stop-stop, qaerga ketyapsiz? Cheklovlar oson!

Asimptotalar misollari elementar funksiyalarning grafiklari bo'yicha birinchi darsda darhol uchrashdi va hozir mavzu batafsil ko'rib chiqilmoqda.

Xo'sh, asimptota nima?

Tasavvur qiling o'zgaruvchan nuqta, bu funksiya grafigi bo'ylab "sayohat qiladi". Asimptot - bu to'g'ri chiziq cheksiz yaqin funktsiya grafigi uning o'zgaruvchan nuqtasi cheksizlikka yaqinlashganda yaqinlashadi.

Eslatma : ta'rif mazmunli, agar sizga matematik tahlil yozuvida formula kerak bo'lsa, darslikka murojaat qiling.

Samolyotda asimptotlar tabiiy joylashuviga ko'ra tasniflanadi:

1) Vertikal asimptotlar, ular ko'rinishdagi tenglama bilan beriladi, bu erda "alfa" haqiqiy sondir. Ommabop vakil y o'qini o'zi belgilaydi,
engil ko'ngil aynish hujumi bilan biz giperbolani eslaymiz.

2) Qiya asimptotlar an'anaviy ravishda qiyalikli to'g'ri chiziqli tenglama sifatida yoziladi. Ba'zan alohida holat alohida guruh sifatida ajratiladi - gorizontal asimptotlar. Masalan, asimptota bilan bir xil giperbola .

Tezlik bilan ketamiz, keling, qisqa avtomatik portlash bilan mavzuni ochamiz:

Funktsiya grafigida nechta asimptota bo'lishi mumkin?

Hech, bir, ikki, uch... yoki cheksiz son. Biz misollar uchun uzoqqa bormaymiz, biz elementar funktsiyalarni eslaymiz. Parabola, kub parabola, sinusoidlar umuman asimptotaga ega emas. Eksponensial, logarifmik funktsiyaning grafigi bitta asimptotaga ega. Arktangens, arkkotangentda ikkitasi bor, tangens, kotangens esa cheksiz songa ega. Grafikning gorizontal va vertikal asimptotalari bo'lishi odatiy hol emas. Giperbola, sizni doim sevadi.

Nimani anglatadi ? Funksiya grafigining vertikal asimptotalari

Grafikning vertikal asimptoti, qoida tariqasida, funksiyaning cheksiz uzilish nuqtasida joylashgan. Hammasi oddiy: agar biror nuqtada funksiya cheksiz tanaffusga uchrasa, u holda tenglama orqali berilgan to‘g‘ri chiziq grafikning vertikal asimptotasidir.

Eslatma : eslatma ikki butunlay boshqa tushunchaga murojaat qilish uchun ishlatiladi. Nuqta nazarda tutilgan yoki to'g'ri chiziq tenglamasi - kontekstga bog'liq.

Shunday qilib, bir nuqtada vertikal asimptota mavjudligini aniqlash uchun bir tomonlama chegaralardan kamida bittasini ko'rsatish kifoya. cheksiz. Ko'pincha, bu funktsiyaning maxraji nolga teng bo'lgan nuqtadir. Darhaqiqat, biz vertikal asimptotalarni funktsiyaning uzluksizligi haqidagi darsning oxirgi misollarida allaqachon topdik. Ammo ba'zi hollarda faqat bir tomonlama chegara mavjud va agar u cheksiz bo'lsa, unda yana - vertikal asimptotani seving va yoqing. Eng oddiy tasvir: va y o'qi (qarang: Elementar funksiyalarning grafiklari va xususiyatlari).

Aniq haqiqat ham yuqoridagilardan kelib chiqadi: agar funktsiya uzluksiz bo'lsa, unda vertikal asimptotlar yo'q. Negadir xayolimga bir parabola keldi. Haqiqatan ham, bu erda to'g'ri chiziqni qayerga "yopishtirish" mumkin? ... ha ... tushunaman ... Freyd amakining izdoshlari jazavaga tushib qolishgan =)

Qarama-qarshi gap odatda to'g'ri emas: masalan, funktsiya butun real chiziqda aniqlanmagan, ammo u asimptotalardan butunlay mahrum.

Funksiya grafigining qiya asimptotalari

Agar funktsiya argumenti "plyus cheksizlik" yoki "minus cheksizlik" ga moyil bo'lsa, oblik (maxsus holat sifatida - gorizontal) asimptotalarni chizish mumkin. Shuning uchun funksiya grafigida ikkitadan ortiq qiya asimptota bo‘lishi mumkin emas. Misol uchun, ko'rsatkichli funktsiya grafigida bitta gorizontal asimptota mavjud va yoy tangensining grafigida ikkita bunday asimptota va har xil.

Bu erda va u erda grafik yagona qiya asimptotaga yaqinlashganda, "cheksizliklarni" bitta yozuv ostida birlashtirish odatiy holdir. Masalan, ... siz buni to'g'ri taxmin qildingiz: .

Umumiy qoida:

Agar ikkita bo'lsa final chegara , u holda to'g'ri chiziq funksiya grafigining qiya asimptotasidir. Agar sanab o'tilgan chegaralardan kamida bittasi cheksiz bo'lsa, u holda qiyshiq asimptota yo'q.

Eslatma : "x" faqat "ortiqcha cheksizlik" ga yoki faqat "minus cheksizlik" ga moyil bo'lsa, formulalar haqiqiy bo'lib qoladi.

Parabolaning qiya asimptotalari yo'qligini ko'rsataylik:

Chegara cheksiz, shuning uchun qiya asimptota yo'q. Limitni topishda e'tibor bering endi kerak emas, chunki javob allaqachon olingan.

Eslatma : agar siz ortiqcha-minus, minus-plyus belgilarini tushunishda qiynalayotgan bo'lsangiz (yoki bo'ladigan bo'lsa), dars boshida yordamga qarang.
cheksiz kichik funktsiyalar haqida, men bu belgilarni qanday qilib to'g'ri talqin qilishni aytdim.

Ko'rinib turibdiki, har qanday kvadrat, kub funksiya, 4 va undan yuqori darajali ko'phad ham qiya asimptotalarga ega emas.

Keling, grafikda ham qiya asimptota yo'qligiga ishonch hosil qilaylik. Noaniqlikni aniqlash uchun biz L'Hopital qoidasidan foydalanamiz:
, bu tekshirilishi kerak edi.

Funktsiya cheksiz o'sganda, uning grafigi yaqinlashadigan bunday to'g'ri chiziq yo'q cheksiz yaqin.

Keling, darsning amaliy qismiga o'tamiz:

Funksiya grafigining asimptotalarini qanday topish mumkin?

1-misol

Funksiya grafigining asimptotalarini toping

Yechimni qulay tarzda ikki qismga bo'lish mumkin:

Men sizga funksiyaning uzluksizligi maqolasida xuddi shunday muhokama qilgan hisoblash texnikasini eslataman. tanaffus nuqtalari. Chegara belgisi ostidagi ifodada "x" o'rniga biz ni almashtiramiz. Numeratorda qiziq narsa yo'q:
.

Ammo denominatorda bu chiqadi cheksiz kichik manfiy son:
, u chegaraning taqdirini belgilaydi.

Xulosa: bir tomonlama chegaralar cheksizdir, bu chiziq funksiya grafigining vertikal asimptoti ekanligini bildiradi.

Birinchi chegara cheklangan, bu "suhbatni davom ettirish" va ikkinchi chegarani topish kerakligini anglatadi:

Ikkinchi chegara ham cheklangan.

Shunday qilib, bizning asimptotimiz:

Xulosa: tenglama bilan berilgan to'g'ri chiziq funksiya grafigining gorizontal asimptotasidir.

Gorizontal asimptotani topish uchun
Siz soddalashtirilgan formuladan foydalanishingiz mumkin:

Agar mavjud bo'lsa cheklangan chegarasi, u holda chiziq funksiya grafigining gorizontal asimptotasidir.

Funktsiyaning numeratori va maxraji bir xil o'sish tartibida ekanligini ko'rish oson, ya'ni kerakli chegara chekli bo'ladi: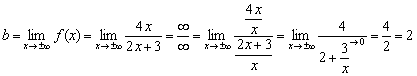

Javob:

2-misol

Funksiya grafigining asimptotalarini toping

Amalda kasr-ratsional funktsiyalar ko'pincha uchraydi va giperbolalar bo'yicha mashg'ulotlardan so'ng biz vazifani murakkablashtiramiz:

3-misol

Funksiya grafigining asimptotalarini toping

Yechim: Bir, ikkita va bajarildi:

Funksiyani formada qayta yozamiz

Nuqtada bir tomonlama chegaralarni toping:

Va shu nuqtada:

Shunday qilib, to'g'ri chiziqlar ko'rib chiqilayotgan funksiya grafigining vertikal asimptotalari hisoblanadi.

2) Agar funktsiyaga qarasangiz , u holda chegara chekli bo'lishi aniq va biz gorizontal asimptotaga ega bo'lamiz. Keling, buni qisqacha ko'rsatamiz:

Shunday qilib, to'g'ri chiziq (abtsissa) bu funktsiya grafigining gorizontal asimptotasidir.

Javob:

Topilgan chegaralar va asimptotlar funksiya grafigi haqida juda ko'p ma'lumot beradi. Quyidagi faktlarni hisobga olgan holda rasmni aqliy tasavvur qilishga harakat qiling:

Grafikning o'z versiyasini qoralamaga chizing.

4-misol

Funksiya grafigining asimptotalarini toping

5-misol

Funksiya grafigining asimptotalarini toping

Bu mustaqil qaror qabul qilish uchun vazifalar. Ikkala grafikda yana gorizontal asimptotalar mavjud bo'lib, ular darhol quyidagi xususiyatlar bilan aniqlanadi: 4-misolda maxrajning o'sish tartibi. Ko'proq hisoblagichning o'sish tartibidan ko'ra, va 5-misolda son va maxraj bir xil o'sish tartibida. Namuna yechimida birinchi funktsiya qiya asimptotalarning mavjudligi uchun to'liq, ikkinchisi - chegara orqali tekshiriladi.

Gorizontal asimptotlar, mening sub'ektiv taassurotimga ko'ra, "haqiqatan ham egilgan" ga qaraganda sezilarli darajada keng tarqalgan. Uzoq kutilgan umumiy holat:

6-misol

Funksiya grafigining asimptotalarini toping

Yechim: janr klassikasi:

1) maxraj musbat bo‘lgani uchun funksiya butun son chizig‘ida uzluksiz bo‘lib, vertikal asimptotlar yo‘q. …Bu yaxshimi? To'g'ri so'z emas - ajoyib! №1 band yopiq.

Ikkinchi chegara ham cheklangan, shuning uchun ko'rib chiqilayotgan funksiya grafigi qiya asimptotaga ega:

Xulosa:

Shunday qilib, funktsiya grafigi uchun cheksiz yaqin to'g'ri chiziqqa yaqinlashadi:

E'tibor bering, u o'zining qiya asimptotasini boshida kesib o'tadi va bunday kesishish nuqtalari juda maqbuldir - cheksizlikda "hamma narsa normal" bo'lishi muhim (aslida, biz aynan o'sha erda asimptotlar haqida gapiramiz).

7-misol

Funksiya grafigining asimptotalarini toping

Qaror: izoh beradigan hech narsa yo'q, shuning uchun men yakuniy yechimning taxminiy namunasini tuzaman:

1) Vertikal asimptotlar. Keling, nuqtani o'rganamiz.

To'g'ri chiziq - da uchastkaning vertikal asimptotasi.

2) qiyshiq asimptotlar:

To'g'ri chiziq - dagi grafik uchun qiya asimptota.

Javob:

Topilgan bir tomonlama chegaralar va asimptotalar ushbu funktsiya grafigi qanday ko'rinishini yuqori aniqlik bilan taxmin qilish imkonini beradi. Dars oxirida to'g'ri chizish.

8-misol

Funksiya grafigining asimptotalarini toping

Ammo hayotda boshqa mo''jizalar sodir bo'ladi:

9-misol

11-misol

Asimptotlar uchun funksiya grafigini ko‘rib chiqing

Yechim: aniq , shuning uchun biz faqat o'ng yarim tekislikni ko'rib chiqamiz, bu erda funktsiyaning grafigi mavjud.

Shunday qilib, to'g'ri chiziq (y o'qi) funksiya grafigi uchun vertikal asimptota hisoblanadi.

2) Qiyma asimptotani o'rganish to'liq amalga oshirilishi mumkin, ammo "L'Hospital qoidalari" maqolasida biz logarifmikdan yuqori o'sish tartibidagi chiziqli funktsiya ekanligini aniqladik, shuning uchun: (xuddi shu darsning 1-misoliga qarang).

Xulosa: abscissa o'qi funksiya grafigining gorizontal asimptotasidir.

Javob:
, Agar;
, Agar .

Aniqlik uchun chizish:

Qizig'i shundaki, ko'rinishidan o'xshash funktsiyaning asimptotalari umuman yo'q (xohlaganlar buni tekshirishlari mumkin).

Ikki yakuniy o'z-o'zini o'rganish misollari:

12-misol

Asimptotlar uchun funksiya grafigini ko‘rib chiqing